在工程应用中,人们对湍流的脉动量往往不太关注,最为关心的是流动要素的时均值。在这类方法里,将非稳态控制方程对时间做平均,在所得出的关于时均物理量的控制方程中包含了脉动量乘积的时均值等未知量,于是所得方程的个数就小于未知量的个数,而且不可能依靠进一步的时均值处理而使控制方程组封闭。要使方程组封闭,必须做出假设,即建立模型。这种模型把未知的更高阶的时间平均值表示成较低阶计算中可以确定的量的函数。这是目前工程湍流计算中所采用的基本方法。这即是常说的“湍流模型”。在湍流模型中又以双方程模型用于除尘设备气流模拟为最多。双方程模型将影响湍流黏性素数的两个特征量k和l转化为另外两个特征量k和Z,并表示成了由微分方程控制的量,其中,Z=kmln,选择不同的m和n,就构成了不同的双方程模型。对于靠近壁面地区的计算来说,以ε方程最为方便,因此在湍流的工程计算中,k-ε双方程模型应用最广。
根据湍动能k及耗散项ε的定义,由因次分析可得:
式中 cD——常数;
k——根据微分方程确定;
l——可由混合长度lm得到。
柯莫哥洛夫-普朗特表达式:
式中 cD——常数;
k——根据微分方程确定;
l——可由混合长度lm得到。
柯莫哥洛夫-普朗特表达式:
式中 cμ和ρ是常数,其他符号同前。
由上两式可以得出:
式中 cμ和ρ是常数,其他符号同前。
由上两式可以得出:
式中 cμ=cμcD。
湍动能k和湍动能耗散率ε是衡量湍流强度及涡尺度的两个湍流统计量,它们是空间坐标的函数,其值可根据模型化后的k方程、ε方程决定。
k方程:
式中 cμ=cμcD。
湍动能k和湍动能耗散率ε是衡量湍流强度及涡尺度的两个湍流统计量,它们是空间坐标的函数,其值可根据模型化后的k方程、ε方程决定。(https://www.xing528.com)
k方程:
方程从左到右分别为:非稳态项、对流项、扩散项、产生项、消失项。其中σk是脉动动能prandtl数,其值在1.0左右,k是单位质量流体湍流脉动动能,湍流黏性系数μt=0.09,ρ为密度,ε为耗散率。
ε方程:
方程从左到右分别为:非稳态项、对流项、扩散项、产生项、消失项。其中σk是脉动动能prandtl数,其值在1.0左右,k是单位质量流体湍流脉动动能,湍流黏性系数μt=0.09,ρ为密度,ε为耗散率。
ε方程:
方程从左到右五项分别为:非稳态项、对流项、扩散项、产生项、消失项。其中,ε是耗散率,μ是分子黏性。
上面所述的k-ε模型,涡黏性弘μt是一个标量,即流场中每一个确定的点处只有一个确定的涡黏项,其值与方向无关,这种模型称之为标准k-ε模型。
方程从左到右五项分别为:非稳态项、对流项、扩散项、产生项、消失项。其中,ε是耗散率,μ是分子黏性。
上面所述的k-ε模型,涡黏性弘μt是一个标量,即流场中每一个确定的点处只有一个确定的涡黏项,其值与方向无关,这种模型称之为标准k-ε模型。
采用k-ε模型来求解湍流问题时,控制方程包括连续性方程、动量方程及k、ε方程与式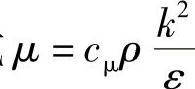 在这一方程组中引入了三个系数(c1、c2、cμ)及三个常数(σk、σε、σT)。这6个经验常数的取值c1=1.44,c2=1.92,cμ=0.09,σk=1.0,σε=1.3,σT=0.6~1.0。
在这一方程组中引入了三个系数(c1、c2、cμ)及三个常数(σk、σε、σT)。这6个经验常数的取值c1=1.44,c2=1.92,cμ=0.09,σk=1.0,σε=1.3,σT=0.6~1.0。
由于采用湍流模型就是要解决如何计算由于脉动所造成的湍流应力问题,所以采用k-ε模型后应力表达式可写成:
采用k-ε模型来求解湍流问题时,控制方程包括连续性方程、动量方程及k、ε方程与式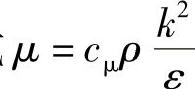 在这一方程组中引入了三个系数(c1、c2、cμ)及三个常数(σk、σε、σT)。这6个经验常数的取值c1=1.44,c2=1.92,cμ=0.09,σk=1.0,σε=1.3,σT=0.6~1.0。
在这一方程组中引入了三个系数(c1、c2、cμ)及三个常数(σk、σε、σT)。这6个经验常数的取值c1=1.44,c2=1.92,cμ=0.09,σk=1.0,σε=1.3,σT=0.6~1.0。
由于采用湍流模型就是要解决如何计算由于脉动所造成的湍流应力问题,所以采用k-ε模型后应力表达式可写成:
其中,δij是Kronecher算符。
通常,在气流相的模拟中均采用湍流模型。
其中,δij是Kronecher算符。
通常,在气流相的模拟中均采用湍流模型。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




