如何进行近似模拟试验：基于粘性流体特性的方法

要实现相似理论中所提出的所有相似条件是非常困难的，有时甚至是根本办不到的，但是由于近似模拟方法的发展，模拟试验才得以实现。

近似模拟试验的根据，就是粘性流体的特性，即稳定性和自模性。

所谓稳定性就是粘性流体在管道中流动，管道截面上的速度分布有一定的规律。速度分布图形与雷诺数、管道形状、所研究的截面与入口的距离有关。试验指出，当流体在直管段中流动时，经入口流过一定长度后，各截面上的速度图形相同。

自模性就是流体的流型也有一定的规律。在直管段中流动的流体，当其流型属于层流运动时，管道截面上的速度图形呈抛物线状；当紊流运动时，管道截面上的速度图形亦呈一种特定的形状，而且流体阻力和压力分布图形保持不变，即不取决于雷诺数的改变，也就是不必遵守雷诺数相等的条件了。这就为近似模拟试验提供了方便的条件。

根据什么来判断是否达到自模条件呢？可以选择下面三种判断方法中的任意一种。

1）所研究的截面上速度分布为固定形状，或者说截面上任意两点的速度比值为常数，即数。

1）所研究的截面上速度分布为固定形状，或者说截面上任意两点的速度比值为常数，即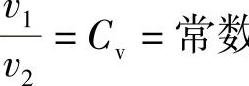数。

2）所研究管段的压力分布曲线为固定的形状，或者说管段中任意两点的压力比值为常数，即。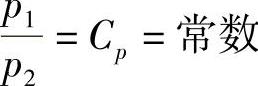

3）Eu数或局部系数ζ值为常数，因而符合阻力平方定律。这三个以第三种为最方便。因为在进行试验中，测量设备的阻力比较方便，而且又经常需要进行的工作，所以能够很容易地判断是否已达到自模条件。

气流分布构件的几何形状越复杂，极限流速越低，对于直的水力光滑管的极限雷诺数Re_极=2200，这就是它的自模范围的起点。

如果实际过程不是紊流情况，需要用模型精确地研究构件中在等温强制流动时的速度分布的话，则必须使模型中的雷诺数等于实物中的雷诺数，即Re_m=Re_sh。

假若在模型中采用的工作流体与实物中的流体相同，那么γ_m=γ_sh，当模型的几何尺寸取为实物的1/10时，在上述条件下，模型中的流速应该比实物中的流速增大10倍。

自由对流传热过程的决定数是Gr×Pr＞2×10⁷时，换热过程与几何尺寸无关，其温度场和流速场等不随Gr×Pr值的大小而变化。这样，就可以用几何相似的缩小模型来研究自由对流过程，而不要求Gr×Pr值相等，只要Gr×Pr＞2×10⁷就可以了。这里必须强调指出，所研究的实际过程首先必须是在自模范围内，才能利用这个规律。

气流分布过程包括流体力学过程与传热过程。要进行模型试验的必要和充分条件可以归结如下几点：

1）几何相似。一般来说，这点是容易做到的，按照实物比例缩小即可。如果所研究的过程是在构件内部发生的，那么应该强调内部尺寸的几何相似。(www.xing528.com)

2）入口条件和边界条件的相似。由于流体的稳定性和自模性，当超过极限雷诺数时，就能够自然地达到入口处的动力相似条件。至于说边界条件相似，将在以后的模型设计计算中对热源和外围结构的传热进行相应的研究。

3）实现系统中物理量的相似。这里的物理量相似是指实物和模型中对应点的介质密度、粘性系数、导热系数以及热容等的比值为常数。如果是绝热过程，那么这个条件就顺利地达到了。对于非绝热过程，由于这些物理量都与介质的温度有关，如果保证了温度场相似，是创造了物理相似条件。

4）起始状态的相似。为了简化，一般都把气流分布过程看做稳定过程，所以需要考虑这个条件。

2）所研究管段的压力分布曲线为固定的形状，或者说管段中任意两点的压力比值为常数，即。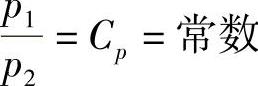

3）Eu数或局部系数ζ值为常数，因而符合阻力平方定律。这三个以第三种为最方便。因为在进行试验中，测量设备的阻力比较方便，而且又经常需要进行的工作，所以能够很容易地判断是否已达到自模条件。

气流分布构件的几何形状越复杂，极限流速越低，对于直的水力光滑管的极限雷诺数Re_极=2200，这就是它的自模范围的起点。

如果实际过程不是紊流情况，需要用模型精确地研究构件中在等温强制流动时的速度分布的话，则必须使模型中的雷诺数等于实物中的雷诺数，即Re_m=Re_sh。

假若在模型中采用的工作流体与实物中的流体相同，那么γ_m=γ_sh，当模型的几何尺寸取为实物的1/10时，在上述条件下，模型中的流速应该比实物中的流速增大10倍。

自由对流传热过程的决定数是Gr×Pr＞2×10⁷时，换热过程与几何尺寸无关，其温度场和流速场等不随Gr×Pr值的大小而变化。这样，就可以用几何相似的缩小模型来研究自由对流过程，而不要求Gr×Pr值相等，只要Gr×Pr＞2×10⁷就可以了。这里必须强调指出，所研究的实际过程首先必须是在自模范围内，才能利用这个规律。

气流分布过程包括流体力学过程与传热过程。要进行模型试验的必要和充分条件可以归结如下几点：

1）几何相似。一般来说，这点是容易做到的，按照实物比例缩小即可。如果所研究的过程是在构件内部发生的，那么应该强调内部尺寸的几何相似。

2）入口条件和边界条件的相似。由于流体的稳定性和自模性，当超过极限雷诺数时，就能够自然地达到入口处的动力相似条件。至于说边界条件相似，将在以后的模型设计计算中对热源和外围结构的传热进行相应的研究。

3）实现系统中物理量的相似。这里的物理量相似是指实物和模型中对应点的介质密度、粘性系数、导热系数以及热容等的比值为常数。如果是绝热过程，那么这个条件就顺利地达到了。对于非绝热过程，由于这些物理量都与介质的温度有关，如果保证了温度场相似，是创造了物理相似条件。

4）起始状态的相似。为了简化，一般都把气流分布过程看做稳定过程，所以需要考虑这个条件。