相似理论基础及粘性流体运动研究

几何相似：相似的概念首选出现在几何学里。几何相似的性质，以及利用这些性质进行的许多计算都是大家所熟知的。例如，两个相似三角形，其对应角彼此相等，对应边互成比例，则可以写成下列关系式：

式中 C₁——几何比例系数或称为相似常数。

由此可以看到，表示几何相似的量只有一个线性尺寸。

力的相似：在几何相似系统中对应的近质点速度互相平行，而且数值成比例，则称此为运动相似。令实物中某近地点的速度为v’，模型中对应近质点的速度为v”，则可写成

式中 C_v——速度比例系数；

τ——时间。

所谓动力相似就是作用在两个相似系统中对应质点上的力互相平行，数值成比例。在实物中，作用力f’引起近质点M’产生运动地；模型中，相似质点M"受力f"的作用而产生相似运动，则作用力f和f"相似，可以写成

为了得到力的相似常数C_f值，需要利用力学基本议程。所有运动物体，不论是通风厂房内的空气运动，不是管道中水的流动以及固体颗粒在气流中的运动等待都遵守牛顿第二定律。该定律的数学表达式为：

f=ma （5-22）

因为加速度值难以从试验中测定，因而把上式中的加速度用速度对时间的微分

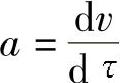来代替。如果时间间隔是有限的，那么a值作用力f值是该时间内的平均值，当dτ无限小，f则是瞬间的作用力。这样，运动议程的形式为

在实物中任意一质点M’，其速度、质量、作用力和时间的数值为v’、m’、f’和τ’，其运动议程为

在相似的模型中，对应一质点M"，其各项取同一单位值，分别为v”、m”、f”和τ”，其运动议程为

再把这两个相似系统中的议程变为相对坐标，为此将实物系统的运动议程相应除以f’₀，m’₀，v’₀和τ’₀，为了保持恒等必须乘相同的数值，得到：

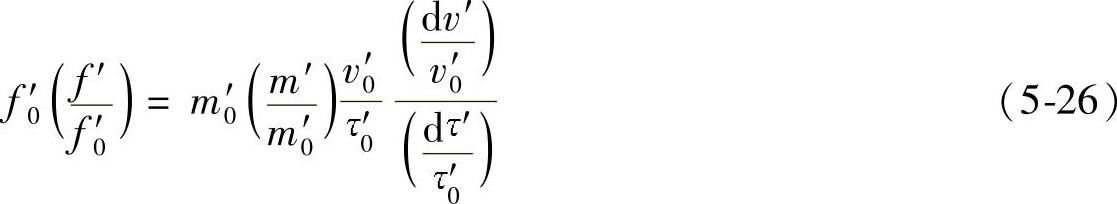
或者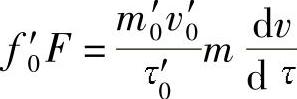

再把所有常数归并到议程式左边，得到：

用同样方法，模型系统中的运动议程经过变换，能得类似的议程式。因为运动是相似的，所以两个议程式中左边项系数应该相等地，其结果是：

此数组称为力的相似常数，亦称牛顿数（Ne）。

为实用方便，用速度代替线性尺寸和时间值，即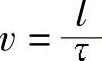，代入公式中，最后得到

这就是牛顿定律，经说明在两个力相似系统中，对应点的作用力与线性尺寸的乘积，除以质量和速度的二次方的数组应为常数值。

牛顿定律是表示物体运动的一般情况，下面分别研究粘性流体运动的个别情况。对于滴状流体或气体，有三种作用力，第一种是质量力（重力f_g），可以认为它是作用于颗粒的重心上；第二种是压力，它作用于颗粒表面并垂直于表面；第三种是接触力（摩擦力f_m）。

如果考虑策略作用，那么作用于立方体上的重力为质量乘重力加速度，即f_g=mg，将f_g代入牛顿数议程中得到

费劳德数取其倒数值的形式

费劳德数表示的是表面重力与惯性力的比值。

如果是由于浮升力产生的运动，就可以用浮力所产生的加速度代替式（5-31）中的重力加速度，则得到阿基米德数：

如果密度差是由于温度不同而产生的，则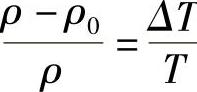，阿基米德数将变为下列形式：

对于压力作用情况，取流体中任意一微小立方体质量，其连长为δl，压力垂直作用其上，假设两对面的压力差为p₁-p₂=△p，则作用于立方体上的总压力差f△_p=δl²△p，小立方体流体质量m=δl³ρ（ρ为该处的流体密度）。将f△_p和m代入牛顿数公式中，可得到欧拉数

欧拉数表示流体压力降与动能之比。

下面研究摩擦力的作用情况。实际流体均有内摩擦或者说粘性，因此当流动时产生摩擦力。取流体单元体积，其立方体每边长为δl，假设平行的两侧面的气流是平行的，又流过上表面的气流速度大于流过下表面的气流速度，由于摩擦的作用，使上表面的气流速度大于流过下表面的气流速度，由于摩擦的作用，使上表面和下表面产生的摩擦力为f₁和f₂。根据牛顿定律，作用单位面积上的摩擦力，f’_m正比于速度梯度，则

比例系数μ称为内摩擦系数。作用于立方体下部界面上的阻力

而作用于上部界面的摩擦力为f_m2-f_m1，按照替换规则可以用f_m1代替它，并代入牛顿数公式中得到

雷诺数取其倒数值

(www.xing528.com)

又经常将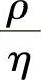表示为动力粘性系数υ，这样便得到常用的形式

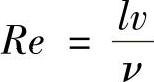
雷诺数表示惯性力与粘性力的比值。

这样可以说，力的相似系统中，以应点的三个相似数Eu、Fr和Re的数值相同，则流体是相似运动。

热相似的意义是指温度场的相似和热流的相似。这里所研究的相似换热过程是简化的情况：假设其辐射换热很小，它与对流换热相比可以略而不计：还假设换热是稳定的，即热表面温度与周围介质的温度不随时间而变化。

温度场相似和换热相似必须在几何相似系统中以及工作流体的动力相似的情况下才能实现。因此，热相似的条件中，当然要包括力的相似条件，即上述所研究的力的相似数Eu、Fr和Re值必须相等。

下面进一步研究热相似的其他条件。在相似的换热体系中，取一微小的立方体（见图5-7），其各边长为δl，所研究的流体与界面平等运动，而传热则与气流方向垂直。通过立方体界面，单位时间通过的流体量等于ρvδl²，由于换热其温度降低△t，因而相应的热交换为

q=Cρvδl²△t （5-39）

式中 C——流体的比热容[J/（kg·k）]。

根据傅里叶公式，单位时间靠导热所带走的热量为

式中 λ——流体的导热系数[W/（m·k）]；

F——导热的面积（m²）；

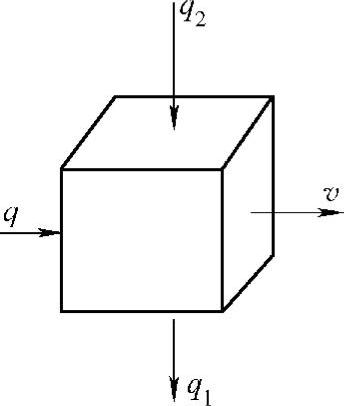
图5-7 微小立方体换热示意

——流体在传热方向上的温度梯度（k/m）。

假设单位时间从微小立方体底界面向它接触的流体给出的热量为

而单位时间经立方体顶面从它所接触的流体得到的热量为

那么立方体同周围介质换热量为二者之差

通过立方体的流体所损失的热量与导热传递的热量彼此相等，然后化简得

式中 a——导温系数（m²），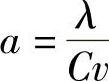

同样，取相对值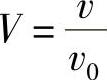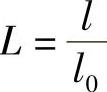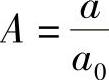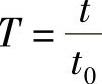，，，，代入上式并经简化整理得到

由此可得出皮克列数

皮克列数表示传热与导热的比值。皮克列数还可以用Re数与Pr数的乘积表示：

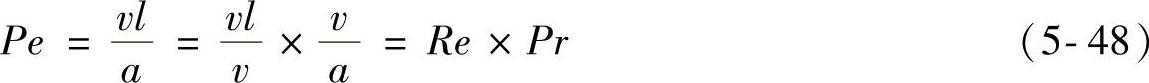
Pr为普朗德数，用Re×Pr代替Pe是比较方便的，雷诺数是流体力学相似的一个数，而Pr数仅与工作流体的物理性质有关。对于原子价相同的气体Pr是常数，对于单原子气体Pr=0.67，对于双原子气体Pr=0.72，对于三原子气体Pr=0.8，对于四原子以上的气体Pr=1。

下面再研究另一个热相似数，它是由界面与直接接触的边界层之间的热交换求得。通过边界层，以导热方式单位面积单位时间传递的热量

从另一方面，以对流方式单位面积单位时间传热量为

q=K（t-t_界） （5-50）

式中 K——对流传热系数[W/（m²·k）]；

t——流体的平均温度（K）；

t_界——界面的平均温度（K）。

以导热方式传递的热量与对流方式的传热量相等，再以同样的方法整理得

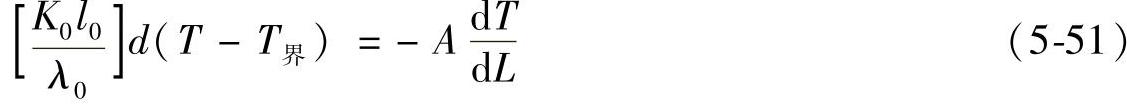
由此求得努塞尔数

由上述一系列推导可以得出，如果两个系统是热相似的，那么除保持几何相似条件外，还必须保持5个数：Re、Er、Eu、Pr和Nu的数值相等。

以上只解决了相似理论中的相似条件问题，即彼此相似的现象必定具有相同的数。但是要进行试验还必须解决建立数之间的关系式问题。

在工程中，经常遇到要用试验方法确定构件的阻力这种情况则属于等温的强制流动，相似数之间的关系为：

Eu=f（Re） （5-53）在研究对流换热的放热系数a值时，对于稳定的条件下，数之间的关系议程式为

Nu=f（Re·Gr·Pr） （5-54）

如果是强制流动，可以忽略Gr的影响，则数之间的关系议程变为

Nu=f（Gr·Pr） （5-55）