理想气体稳定流动的基本方程：柏努利方程式

1.连续性方程

空气流动时如果在管道任一截面上，状态参数压力p、密度ρ、温度T及流速v等都均匀一致且只沿流动方向发生变化，这种流动叫做一维稳定流动。

连续性方程是质量守恒定律在流体流动中的应用，即

对于管道任意两个截面1和2，则有

ρ₁v₁A₁=ρ₂v₂A₂ （5-13）

上面三个计算式中，q_m、ρ、υ、A分别代表气体的质量流量、密度、比容和管道截面积的关系。该方程说明了气体在管内流动时，流量、流速、截面积和密度（或比容）之间的关系。

对不可压缩流体密度ρ（或比容υ）可视为常数，则上式可简化为：

υA=常数

从式（5-12）可以看出，在流速不太高时，流速与管道截面积成反比，即管道截面积减少时，气体的流动速度增加。反之，管道截面积增大时，流动速度降低。

2.柏努利方程式

柏努利方程式是气体流动时的机械能守恒定律在气体力学上的应用。理想不可压缩流体作稳定流动时，柏努利方程的微分形式是：

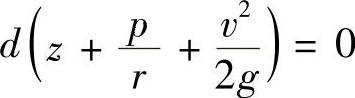
积分后得：

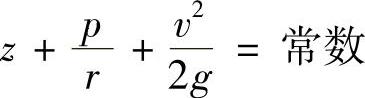
或写成

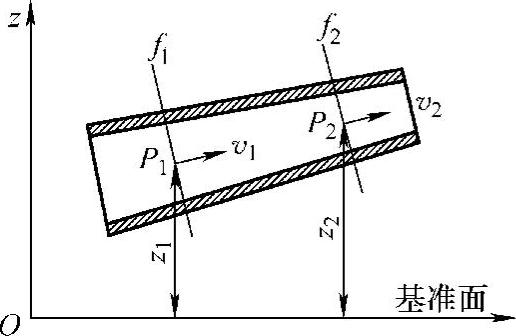
如果气体是在管路中稳定流动时，则管路任意两端截面f₁、f₂（见图5-3）的柏努利方程式可表示为：

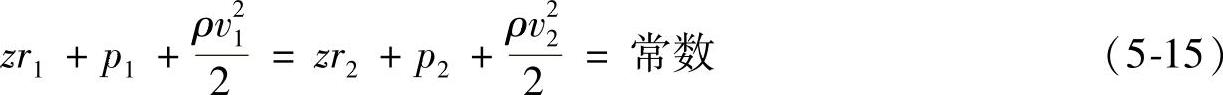
式（5-14）、式（5-15）即是非压缩性的理想气体的柏努利方程式。其各项单位是Pa，表示每1m³气体所具有的各种能量。式中各项的意义为：

zr，zr₁，zr₂——任意截面及f₁、f₂截面处单位体积气体所

具有的位能，即气体所具有的位压能；

p，p₁，p₂——任意截面及f₁、f₂截面处单位体积气体所

具有的压力能，即气体具有的静压能；

(www.xing528.com)

图5-3 气体在管路中稳定流动时选取的任意两截面

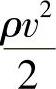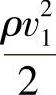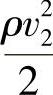，，——任意截面及f₁、f₂截面处单位体积气体所具有的动能，即气体所具有的动压能；

v，v₁，v₂——任意截面及f₁、f₂截面上气体的平均流速（m/s）。

实际流体是具有粘性的，在流动过程中因摩擦和冲击而要消耗部分能量，此时列柏努利方程式时必须考虑能量的损失：

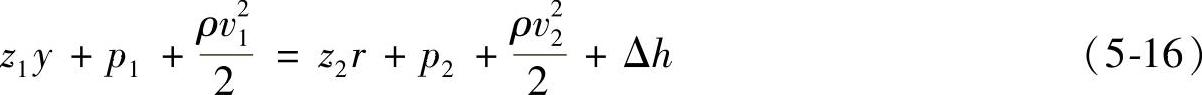
式中 △h——流体在f₁、f₂截面之间流动过程中的能量损失（Pa）。

式（5-16）即为实际气体的柏努利方程式。

在许多连续耗气的气动装置中，总是将排气管直接与大气接通，此时大气状态必然会对管内气体的各种能量产生影响；当大气处于静止状态时，管内气体具有的各种能量均为相对能量——即所谓的“压头”，它们之间的转换仍遵守能量守恒定律。因此管内实际气体的柏努利方程式应改写为如下形式：

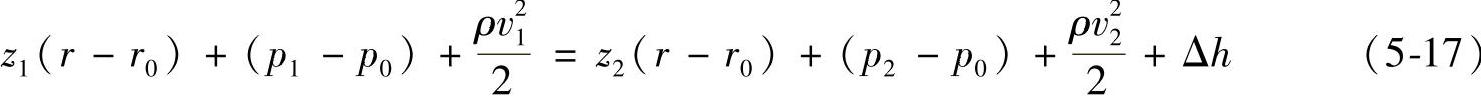
式中 r₀——管外大气的重度；

p₀——管外大气的压力；

（p₁-p₀）、（p₂-p₀）——f₁、f₂截面处的静压头；

z₁（r-r₀）、z₂（r-r₀）——f₁、f₂截面处的位压头；

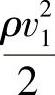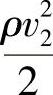、——f₁、f₂截面处的动压头。

另外，当气体在水平管道内流动且直接与大气连通时，此时z₁=z₂，v₂=0，即方程式（5-17）等号右边的速度项为零，柏努利方程便有了如下形式：

式中 p₀——速度为零处的压力，即大气压力。

柏努利方程式说明了理想气体在稳定流动时的能量守恒定律，也是用来分析气体在管路中稳定流动时能量的变化的基本方程式。它告诉我们不仅任意截面上各种能量之和不变（等于常数），而且各种能量之间可以相互转换，一种能量增加，另一种能量必然减少。

对柏努利方程式所揭示的能量转换关系，我们可以得出以下结论：

1）实际气体在管道中作稳定流动时，动压头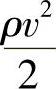的变化取决于管道截面积和气体温度、截面积不变的等温流动时，动压头不改变；截面积变化或变温流动时，动压头要发生变化，并直接引起静压头（p-p₀）的变化；

2）位压头z（r-r₀）的变化取决于高度和温度的变化，等温水平流动时位压头不变；高度变化或变温流动时，位压头要发生变化，并直接引起静压头（p-p₀）的变化；

3）能量损失△h是由动压头直接转变的，而动压头的损失则由静压头或位压头补偿，能量损失最终转变为热能，因此是不可逆的；

4）动压头、位压头、能量损失的变化都会影响静压头的变化；但是在强制流动的条件下，一般认为静压头（p-p₀）是促使气体流动的原动力，所以静压头的变化将会引起其他压头的改变。