交流电路功率定义详解

(1)瞬时功率 设电路电流的参考方向为电压降的方向，则电流电压稳态信号可表示为：

u=U_mcos（ωt+θ_u）

i =I_mcos（ωt+θ_i） (A-16)式中 θ_u——电压相位角；

θ_i——电流相位角。

瞬时功率可表示为

p=ui

以电流最大值作为o时刻，对式(A-16)变换如下：

u=U_mCOS（ωt+θ_u-θ_i）

i=I_mcosωt

带入p=ui得到瞬时功率表达式：

由上式可知，瞬时功率的频率是电压和电流频率的2倍，即电压或电流完成1个周期变化时，瞬时功率完成2个周期的变化。瞬时功率也可以为负值，意味着存储于电容或电感中的能量获得释放。

(2)有功功率 有功功率表示为

由上式可知，瞬时功率的频率是电压和电流频率的2倍，即电压或电流完成1个周期变化时，瞬时功率完成2个周期的变化。瞬时功率也可以为负值，意味着存储于电容或电感中的能量获得释放。

(2)有功功率 有功功率表示为

把P带入得

把P带入得

有功功率描述了电路将电能转变为其他形式能量的功率。式（A-17）可重写为

有功功率描述了电路将电能转变为其他形式能量的功率。式（A-17）可重写为

p=P十Pcos2ωt 2 Qsin2ωt 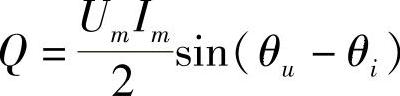能量，但对外并没有做功。

（3）功率因素θ_u 2θ_i称为功率因数角，其余弦函数称为功率因数，简写为p f，其正弦函数称为无功功率因数，简写为r_f，即

p f=cos（θ_u 2θ_i）

r_f=sin（θ_u 2θ_i）（A-18）

（4）复功率 复功率是有功功率和无功功率的复数和，即(www.xing528.com)

S=P十jQ

复功率的模称为视在功率，即

p=P十Pcos2ωt 2 Qsin2ωt 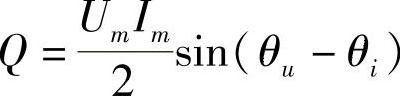能量，但对外并没有做功。

（3）功率因素θ_u 2θ_i称为功率因数角，其余弦函数称为功率因数，简写为p f，其正弦函数称为无功功率因数，简写为r_f，即

p f=cos（θ_u 2θ_i）

r_f=sin（θ_u 2θ_i）（A-18）

（4）复功率 复功率是有功功率和无功功率的复数和，即

S=P十jQ

复功率的模称为视在功率，即

有功功率表示能量的有用输出，视在功率表示提供这样的有功功率需要多大的伏安容量。

视在功率、有功功率和无功功率之间的关系可通过功率三角形描述，如图A-7所示。

有功功率表示能量的有用输出，视在功率表示提供这样的有功功率需要多大的伏安容量。

视在功率、有功功率和无功功率之间的关系可通过功率三角形描述，如图A-7所示。

图A-7 功率三角形

令Z_L为负载阻抗，Z_Th为电源端等效为戴维南电路的等效阻抗，U_Th为等效电压，当

Z_L=Z^∗_Th

即负载阻抗等于戴维南阻抗的共轭复数时，可以传输最大的有功功率。

图A-7 功率三角形

令Z_L为负载阻抗，Z_Th为电源端等效为戴维南电路的等效阻抗，U_Th为等效电压，当

Z_L=Z^∗_Th

即负载阻抗等于戴维南阻抗的共轭复数时，可以传输最大的有功功率。