开短路法的基本原理

当被测电缆终端开路时，其输入阻抗可由传输方程求得

Z∞＝Z_Cthγl （8-1）

式中 Z_C——回路的波阻抗；

γ——回路的传播常数；

l——回路长度。

当被测电缆终端短路时，其输入阻抗为

Z∞＝Z_Cthγl （8-2）

由式（8-1）与式（8-2）可得

则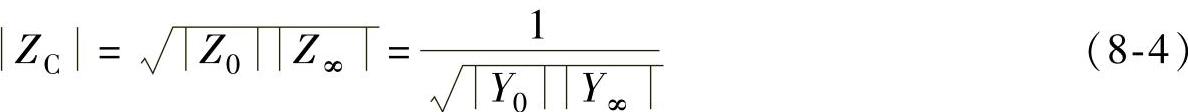

式中 φ∞、φ₀——终端开路和短路时，输入阻抗的相角；

φ_C——波阻抗的相角。

从式（8-1）及式（8-2）中还可得

设 thγl＝Te^jφT＝Tcosφ_T+jTsinφ_T （8-7）

则

αl+jβl＝arcth（Tcosφ_T+jTsinφ_T） （8-10）

按求复变反双曲线正切函数值的计算公式，则

u+jv＝arcth（X+jY） （8-11）

则

令 u＝αl，v＝βl，X＝Tcosφ_T，Y＝Tsinφ_T

则

这里要注意的是，tg2βl是个周期性函数，按式（8-15）计算βl可以有很多数值，所以式（8-15）的完整写法应为

那么n应为多少合适？应根据公式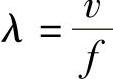计算波长，再估算线路全长内大约包含几个波长，然后按公式（8-16）计算得到的βl应与其相对应。

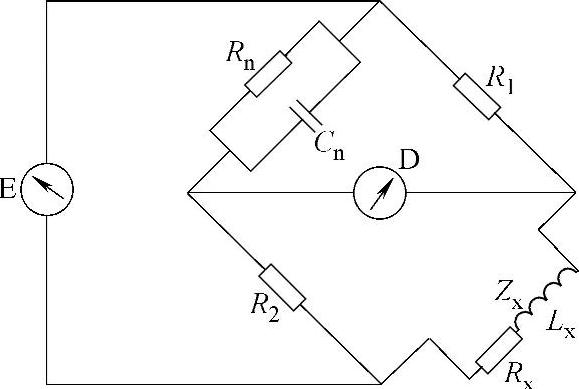
图8-2 阻抗电桥原理图

R₁、R₂—固定电阻 R_n、C_n—平衡网络元件 Z_x—被测电缆阻抗 E—振荡器 D—指示器

在求出二次参数Z_C和γ之后，可再求出一次参数。(https://www.xing528.com)

由于 Z_Cγ＝R+jωL （8-17）

令 Z_Cγ＝Z_Cγe^{j（φc+φγ）} （8-19）

则 R＝|Z_Cγ|cos（φ_c+φ_γ） （8-21）

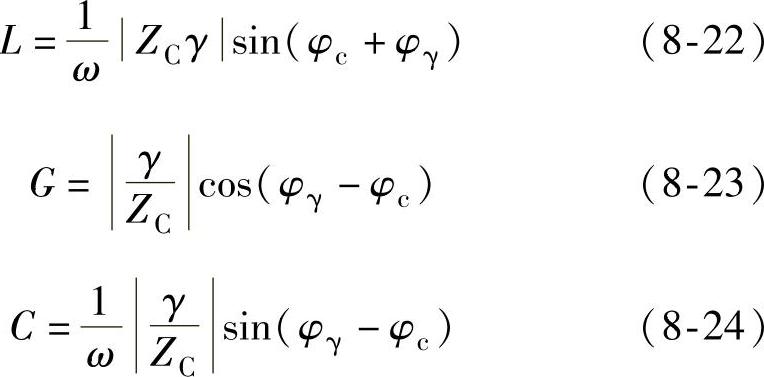
1）用CD-5型阻抗电桥测低阻抗时，如图8-2所示。

当电桥平衡时，

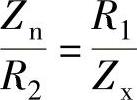
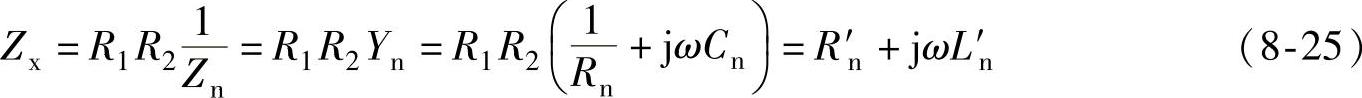
式中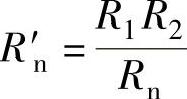，L′_n＝R₁R₂C_n——电桥平衡时度盘上实读的电阻分量和电抗分量值。它们即为被测阻抗的电阻分量和电感分量。

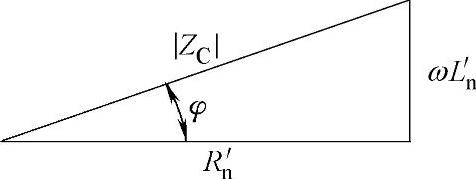
图8-3 阻抗三角形图

式（8-25）用图8-3表示，则为

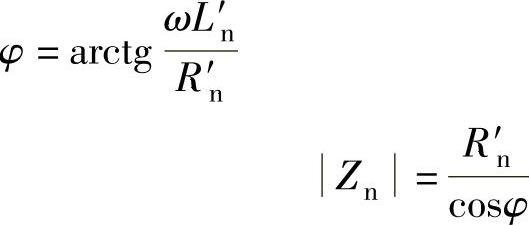
2）用CD-6型电纳电桥测容性导纳，如图8-4所示。

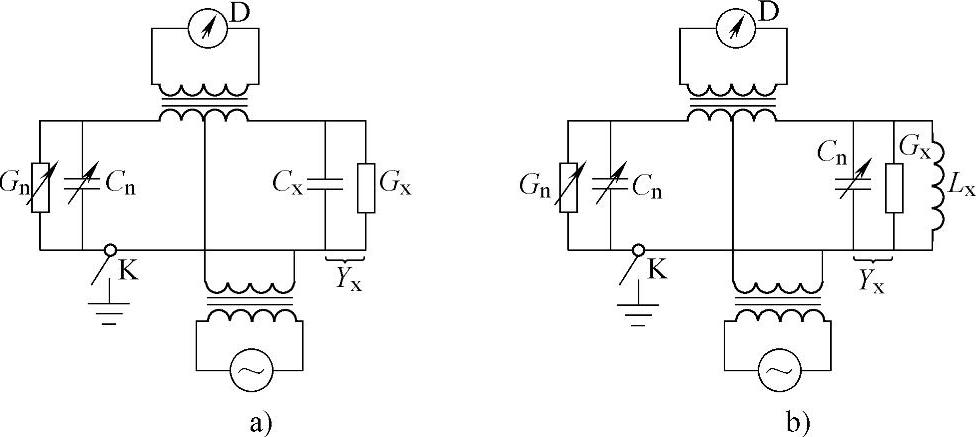
图8-4 导纳电桥原理图

a）测容性导纳 b）测感性导纳

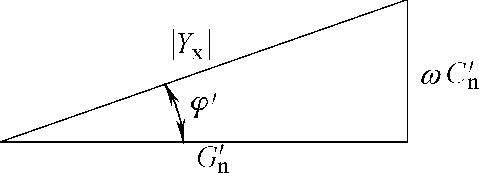
图8-5 导纳三角形图

由图8-4a可知，当电桥平衡时，

Y_x＝Y_n＝G_n+jωC_n

导纳三角形如图8-5所示。

用图8-5表示为

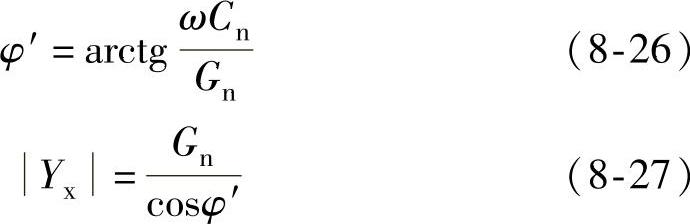
3）用CD-6型电纳电桥测感性导纳。

由图8-4b可知，当电桥平衡时，

Y_x+jωC_n＝G_n

Y_x＝G_n-jωC_n

用图8-4所示的三角形表示为