电缆绞合的基本知识

在电缆的制造过程中，将线芯绞合成组（对绞组、星绞组、复对绞组等），再由组按层绞合成整个缆芯的目的，除了增加电缆的可弯曲性外，主要还是使电缆各个回路间的电磁耦合的相互干扰得到减小。

电缆回路间的耦合有以下几种：

组内耦合（同一线组内回路间的耦合）；

邻近耦合（同一层中的不同线组的回路间的耦合）；

层间耦合（不同层的各线组的回路间的耦合）。

电容耦合和电感耦合都可用干扰回路的导线（1～2）和被干扰的回路的导线（3～4）间的距离来表示，由式（5-35）和式（5-40）可知，不存在电容耦合和电感耦合的条件是：

要达到上述条件必须是

a₁₄＝a₁₃a₂₃＝a₂₄ （5-64）

或

a₁₄＝a₂₄a₂₃＝a₁₃ （5-65）

再或者使下列等式得到满足：

a₁₄a₂₃＝a₁₃a₂₄ （5-66）

显然，当四根导线相同的绝缘单线以星形绞对，以上条件能自动满足，这时干扰回路的两根导线1～2和被干扰回路的两根导线3～4正好始终在一对相互垂直的轴上，绝缘单线以星形绞对组的情况如图5-25所示。因此，在这类绞合中发生组内耦合仅是由于制造时的误差和不均匀引起，而与绞合节距无关。

复绞对四线组通常是由两个相同绞距的对绞组以90°为相移扭绞而成，复对式四线组的绞合情况如图5-26所示。

由图5-26可以看出，组内两回路基本上符合a₁₄a₂₃＝a₁₃a₂₄的条件，这就是说，复对绞或四线组内两线对以同一绞距扭合，是可以减少组内回路间的相互干扰的。

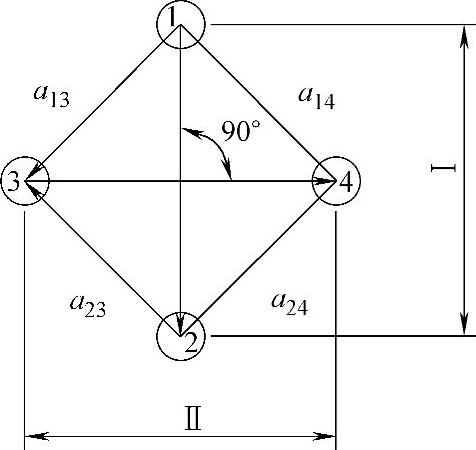
图5-25 绝缘单线以星形绞对组的情况

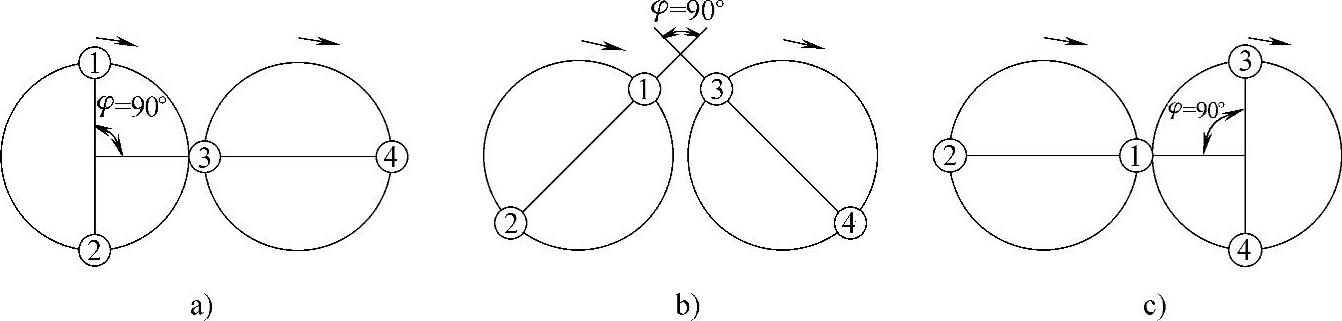
图5-26 复对式四线组的绞合情况

a）第一位置 b）第二位置 c）第三位置

对于组间的邻近耦合或层间耦合的情况将是如何？是否可以用相同绞距的线组绞合成电缆呢？为此，我们先来看如图5-27所示的回路组成情况。

图5-27a表示了相互紧靠且平行放置的两个回路，其中一个回路（被串回路Ⅱ）的两根导线在中点交叉。

根据前面已提到的线路交叉的结论可知，由于回路Ⅱ的交叉，流过干扰回路导线1的电流I₁，将不对回路Ⅱ发生干扰作用，同样，流经被干扰回路导线2的电流对干扰回路也不会发生干扰影响。

因此，两个互靠近和并行放置的回路，若变动其中一个回路的两根导线的位置（交叉）时，一般可消除回路间的干扰，而且，这种位置的变动越是频繁（即交叉越多），则回路间的干扰也越小。

现在来看图5-27b，不是一个回路，而是两个回路在同一点交叉的情况。从图可知，由于导线1和3及导线2和4，始终处于各自并行，因此，线路等于没有进行交叉一样，干扰现象照样发生，当绞距相同的两个线组相互靠近和并行放置时，正好与此相当，所以也不能减轻线路间的相互干扰。

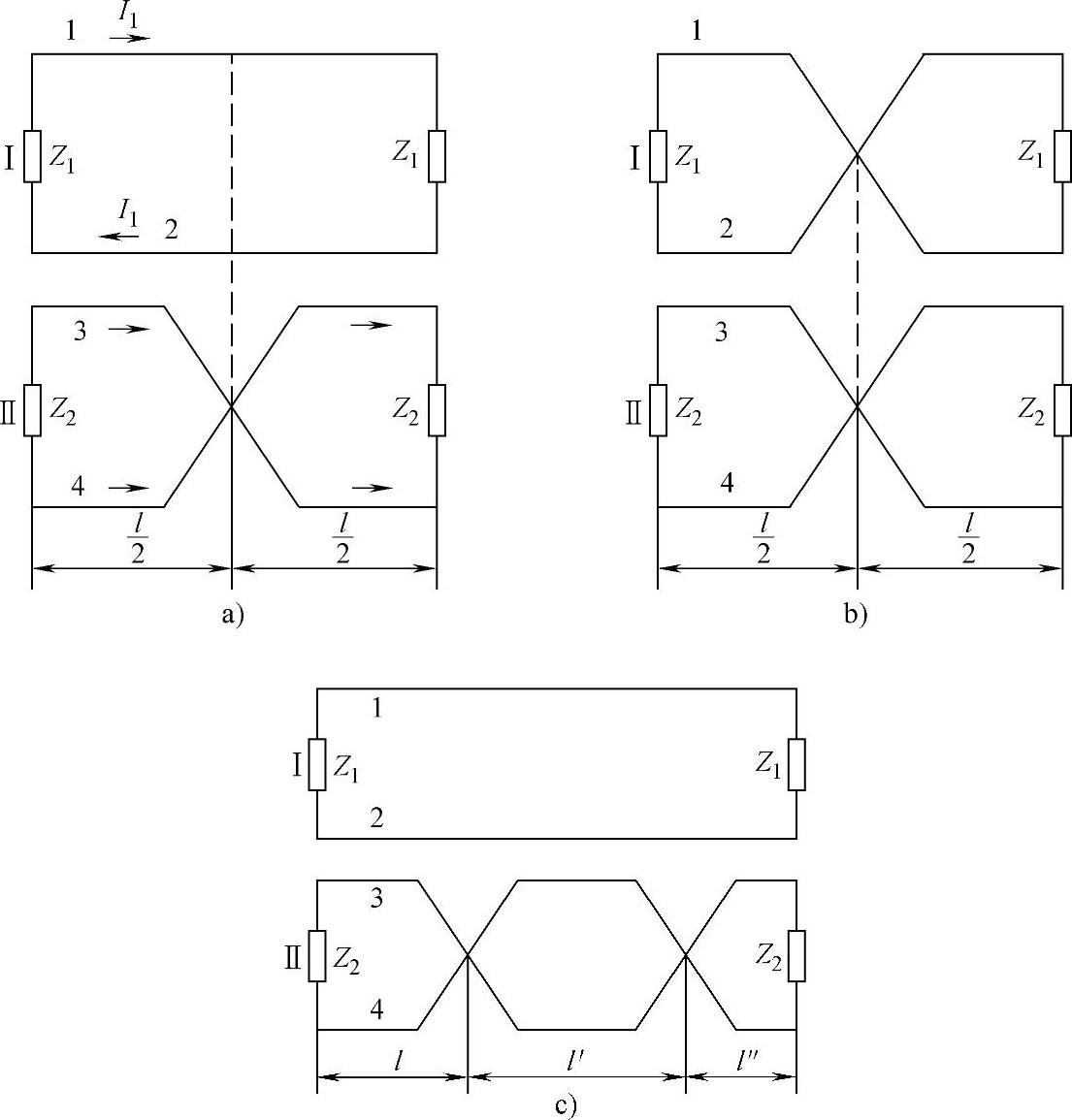
图5-27 回路组成情况

a）并行放置的两个回路，其中一个回路在中点交叉 b）两个回路在同一点交叉 c）回路交叉间距彼此不配合形成不平衡线段

再来看图5-27c，回路交叉间距彼此不配合而形成不平衡线段的情况（原来交叉好的线路，在任意点切断就会出现与此相当的情况）。

从图5-27c可见，在l和l′两段（l＝l′）间发生的干扰作用可以相互对消，但是在l″这段长度内，却仍然与没有交叉时一样，因此同样可以发生干扰作用，而且这个线段越长，则造成的干扰也越大。这段长度的线段，称为电缆线路的不平衡长度。

经以上分析，线路的交叉只有当各个回路有相互配合的特种交叉间距，而将回路的不平衡段减至最小时才有效。

在本质上，电缆的绞合与交叉相似，后者是在一些间距一定距离的点上变换线的位置（例如架空明线的情况），而前者则是沿电缆的整个长度方向均匀地转换线芯的相对位置。因此，要减小电缆内邻近线组间的干扰影响，也只有当邻近各线组的绞距既不相同，又同时满足某种特定的关系时，在使线路的不平衡长度减至最小的情况下才有可能。(https://www.xing528.com)

在通信电缆中，各相邻回路或线组的绞合间距通常是不一样的，并且是依照被称为平衡节或防卫节的段落来进行选择和配合的。

所谓防卫节（或平衡节）l_s，是表示电缆的一段，在这一段长度内，基本上防止了电缆回路间的相互干扰。整根电缆就是由许许多多个这样的段落连续而成，从而防止了回路间的相互干扰。

防卫节与绞合间距的关系如下：

式中 h_a、h_b——两个回路（或线组）自身的绞合节距；

B——h_a、hb的最大公约数。

显然，防卫节l_s实质上也就是h_a、h_b的最小公倍数。

例如，绞距分别为h₁＝50mm和h₂＝40mm的两个线对Ⅰ及Ⅱ，最大公约数B＝10mm，最小公倍数是200mm。两回路间的防卫节如图5-28所示，在l_s长度内，两线对有整数倍的旋转扭矩，因此在电缆段l_s的终端，各芯线位置和它在始端相同，在l_s电缆长度内，各芯线的位置及线距a₁₃、a₁₄、a₂₃及a₂₄经常改变，在l_s的以后各段防卫节中，各芯线又重复出现这一段的情况。因此，我们只要研究一个防卫节中l_s长度内的情况就可以。

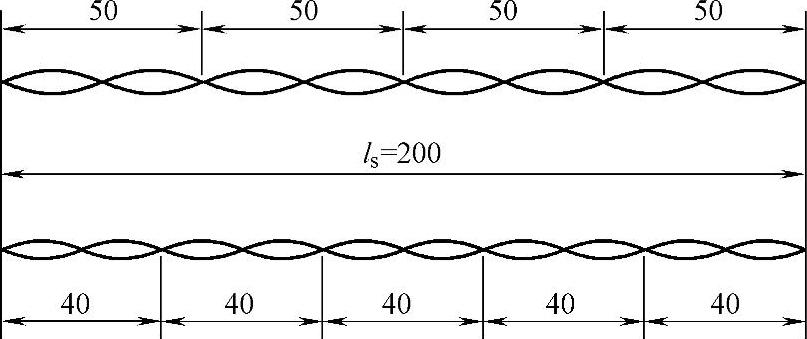
图5-28 两回路间的防卫节

在防卫节l_s内，各芯线间的距离随长度而变化，与各线组扭矩有关。如果适当地选择各线组的绞距，就可以在防卫节内沿着电缆长度方向满足消除耦合的条件。心线间的距离曲线如图5-29所示，前半节a₁₃的变化，正好重复着后半节a₁₄的变化，即在防卫节内沿着电缆长度方向有a₁₃＝a₁₄，同样也有a₂₃＝a₂₄，从而满足了不存在电容耦合和电感耦合的条件，回路间的干扰减至最小。

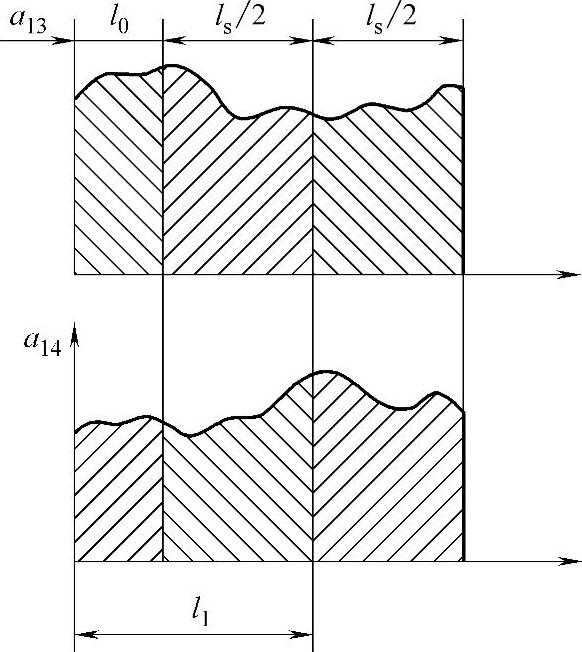
图5-29 心线间的距离曲线

在低频电缆中，回路间的干扰，实际上几乎只是由电容耦合引起的，而电容耦合对邻近的一些线组才有影响，对较远一些线组的这种影响由于十分微小可忽略。因此，只要使相邻线组的绞距相互间得到配合，就可减轻相互的干扰。实际生产中，按同心层绞合时，是采用两个不同的但又相互配合的绞距h₁和h₂，使它们轮流交替来实现的，只是当同一层中的线组数出现奇数时，才必须采用第三个与上面两个绞距相互配合的绞距h₃，用于最后余下的一组。

线路之间的磁场影响可以传得很远，因此，由磁耦合产生的干扰可在电缆中的各个线组间发生。在供高频使用的长途通信电缆中，其中磁耦合的值很大，因此，必须要使每一线组的绞距与其他各线组的绞距配合好。

相邻线组间绞距配合的计算公式为

对位于同一层内的星绞四线组：

对于同一层中的复对绞组：

式中，w及v为大于零的任意整数，复对绞组公式中的h′_a及h′_b表示相邻两线组内线对的绞距。

如果，必须使位于不同层内的线组彼此配合的绞距，则除了上面所列的关系外，还必须保证一附加条件：

式中，H₁和H₂为第一层和第二层的层绞间距，而w和t为大于零的任何整数。

根据以上所列的公式可以计算和配合任意两个线组的绞合间距h_a和h_b，或两层的绞合间距H₁和H₂。实际上，电缆是由线组（即元件）组合而成，并且所有线组都应防止相互干扰，一般给定了第一组以任意的绞合间距后，只要采用不同的v和w就可以算出很多个绞距。一般而言，这些绞距中的任意一个都能保证电缆回路应有的防卫性。但是，这也只有在电缆制造长度段内含有整数个防卫节的理想情况下才有可能。然而，这种理想情况是不可能达到的，因为在制造或敷设电缆时，都可能在任意点切断电缆，这样就不可避免地出现前面曾提到的所谓不平衡长度的干扰影响。为了要减小这种影响，只有使选择的绞距能得到最短的防卫节l_s，这样，当电缆在任意端切断后，所余的不平衡长度就小，由此引起的耦合也小。要l_s很短，线组的绞距就必须要短，而线组绞距短的结果将使电缆的总体增大。在实际中通常是按照这样的步骤来选择绞距：

1）先在实验证明为最有利的绞合间距范围内（例如，对星绞四线组是100～300mm），选择一个较中间的绞距作为计算的第一个节距h₁。

2）利用上述节距按式（5-69）或式（5-70）或式（5-71）对应不同的v和w计算出其他各个节距h₂、h₃等。

3）在有利范围内，根据式（5-67）选择可得到的最短防卫节的绞合节距。

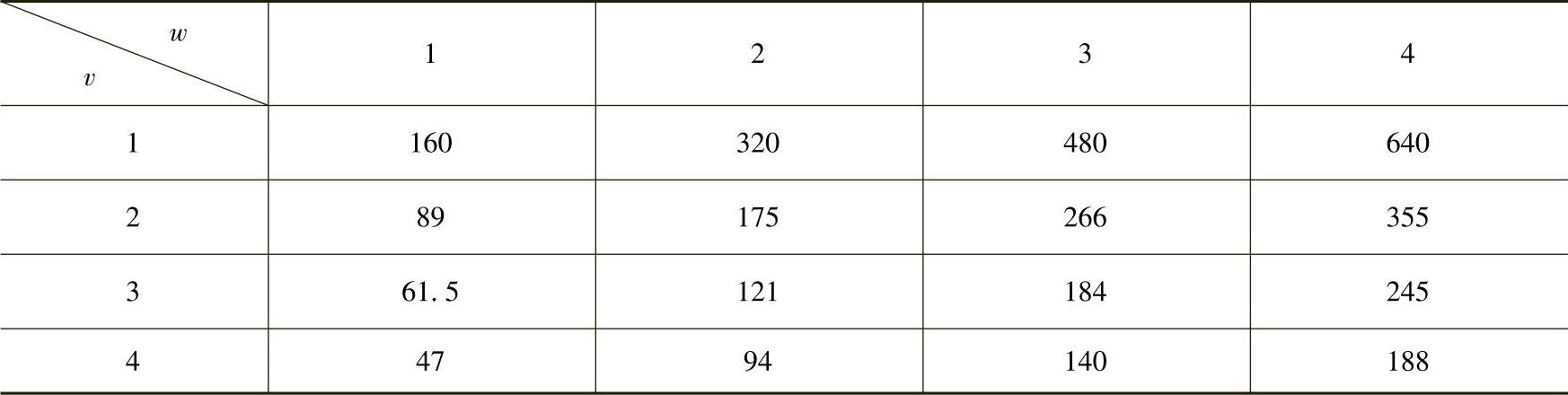
表5-4列出了当h₁取200mm，v和w分别为1～4时，4×4星绞电缆线组绞合节距的计算结果。最后确定的绞距为：h₁＝200mm、h₂＝160mm、h₃＝175mm、h₄＝125mm，允许公差是±5mm。

表5-4 星形四线组绞合间距的计算结果 （单位：mm）