射频电缆在用于天线馈线等大场合时,电缆所传输的平均功率很大,致使电缆发热而内部温度升高,当温度超过绝缘介质所能承受的温度时,便致使电缆产生热损坏。
电缆热损坏的形式是:过热使介质变软,内导体可能偏心,严重时会与外导体短路,过热也可使电缆各部分热膨胀程度不同而引起机械损坏,还可能使介质发生化学损坏,使电缆寿命下降。因此,必须避免内部过热,也就是额定平均功率要受到温升的限制。
电缆的额定平均功率(或称平均传输功率)是电缆长期运行而不发生热损坏的平均功率的规定值。也可以说是在给定的环境条件和稳定状态下,电缆具有匹配负载的绝缘达到它所允许的温升时,电缆所能传输的功率。额定平均功率是大功率射频电缆的重要特性之一。
电缆的额定平均功率取决于电缆内部的发热情况及其散热的能力,并且与介质材料的耐高温能力有关。电缆内部发热除与传输功率大小有关外,还与电缆的衰减值有关,电缆的衰减越低,则可以传输的功率也越大。电缆的散热能力取决于电缆的热力学特性以及敷设条件、环境温度等。而介质的耐温能力越高,则可传输的功率也越大。因此,为求取最大功率射频电缆的额定平均功率,必须要进行计算。
当高频能量在电缆中传输时,在内导体、绝缘及外导体中均会发热,使电缆温度升高(内导体温度为最高),同时电缆也向外散热,当达到热平衡时,电缆的温度不再上升。
研究电缆的上述发热过程,可以采用类似于欧姆定律的关系公式,即

式中 W——电缆中产生的总热流(W/cm);
t内——电缆的最高允许温度(℃),电缆中的绝缘层应该能够长期在此温度下保证足够好的电气和机械性能;
t媒——电缆周围媒质的温度(℃);
S——热流从电缆内导体流到周围媒质所遇到的总热阻(热欧·厘米)。
由上式可知,为了确定某一电缆所允许的传输功率,应先求t内 和t媒 值,再求电缆中发出的热流及各结构元件和周围媒质的热阻值。图4-28所示是计算热流及热阻用的同轴电缆示意图。
同轴射频电缆中所产生的热流包括以下几部分:
1)内导体中的热流Wa;
2)电缆绝缘层中的热流WG;
3)外导体中的热流Wb。
导体中热流是内、外导体的有效电阻引起的热损耗。绝缘层中的热流是绝缘材料的介质损耗及导电损耗。
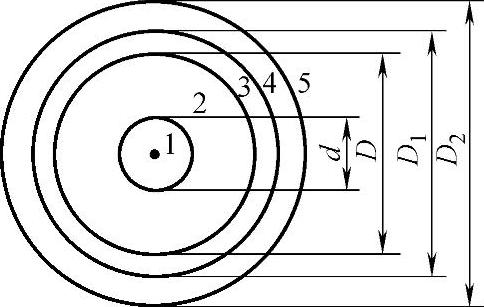
图4-28 计算热流及热阻用的同轴电缆示意图
1—内导体 2—绝缘 3—外导体 4—护层 5—周围媒质
因此热流可用电缆中的热损耗来表征。在一般情况下,热损耗可以由下式确定:

式中 I——电缆回路中的电流;
U——电缆回路中的电压;
Ra——内导体的有效电阻;
Rb——外导体的有效电阻;
G——同轴回路的绝缘电导。
当同轴射频电缆具有匹配负载时(即行波传输或无反射传输),下列各式是适用的:
波阻抗
衰减常数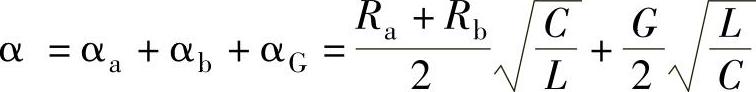

式中 αa、αb、αG——内导体、外导体和绝缘层的衰减常数。
由式(4-58)可得
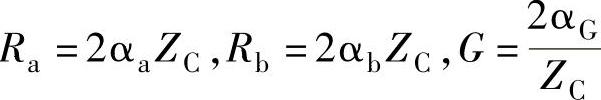
则式(4-56)可改写为

电缆的总热阻包括有绝缘热阻S超、护层热阻S护 和电缆向周围媒质散热的热阻S媒。内、外导体的热阻和金属护层的热阻与上述这些热阻相比可以忽略不计。
对于同轴射频电缆,绝缘层和外护层单位长度的热阻可由下列公式确定:

式中 D——绝缘层的外径(mm);
d——绝缘层的内径(mm);
D2——外护层的外径(mm);
D1——外护层的内径(mm);
ρ超——绝缘介质的热阻系数(热欧·厘米);
ρ护——外护层材料的热阻系数(热欧·厘米)。
热阻的单位为“热欧”,1热欧表示由一单位立方体的一个面,在温度差为1℃时,将1W热流移至另一个方向1cm远的侧面时所遇到的阻力。
射频电缆常用的绝缘即护层材料大的热阻系数见表4-7。
向周围媒质散的热阻决定于媒质情况(即电缆敷设的环境)。一般大功率射频电缆,大部分是用于架空敷设,这时单位长度的热阻为

式中 D2——电缆的外径(cm);
kh——电缆表面的散热系数;
θ0——内导体达到最高允许温度时,电缆外表面和周围环境的温差(℃)。
表4-7 常用材料的热阻系数(热欧·厘米)(https://www.xing528.com)

电缆表面的散热系数kh如图4-29所示。
图4-29所示是一根电缆单独架设时的数值,如两根电缆并排架空敷设,kh值应减小30%,如三根电缆在一起,则kh应减小40%。
当电缆埋地敷设时,向周围媒质散热的单位长度的热阻为

式中 ρ——土壤的热阻系数(热欧·厘米);
l——埋地深度(cm);
D2——电缆外径(cm)。
下边讨论电缆各结构元件中发出的热流及其传导情况。
同轴射频电缆的等效热路图如图4-30所示。
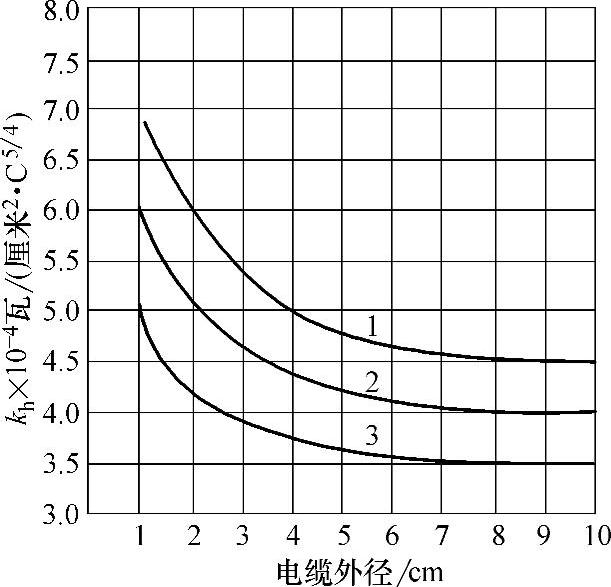
图4-29 电缆表面的散热系数kh
1—塑料护套 2—裸铅套 3—铜线编织
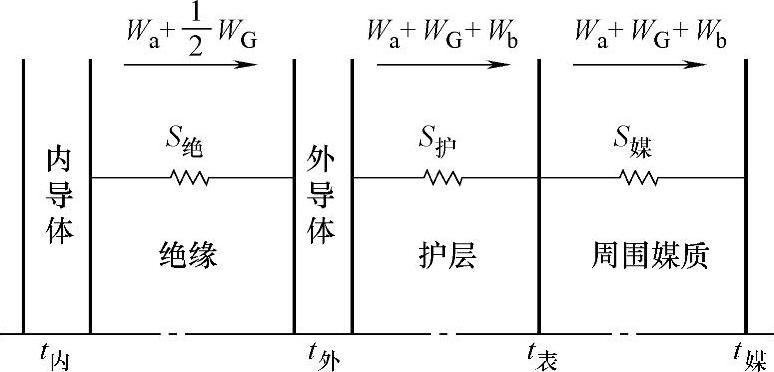
图4-30 同轴电缆等效热路图
从图4-30中可以看出,内导体热流Wa流经绝缘热阻S绝、护层热阻S护和周围媒质热阻S媒。外导体的热流Wb只流过S护和S媒。绝缘中热流WG除流过S护 和S媒 外,还应考虑流过绝缘的热阻S绝,但因WG是在整个绝缘中产生的,WG并不是流过整个的S绝,因此,热流WG在绝缘中引起的温度降与热流通过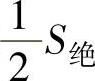 所引起的温度降是一样的,所以绝缘中的热流WG的总热阻为S护、S媒与
所引起的温度降是一样的,所以绝缘中的热流WG的总热阻为S护、S媒与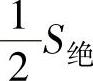 之和。
之和。
根据热欧姆定律,电缆最高允许温度和周围媒质温度的温差由下式确定
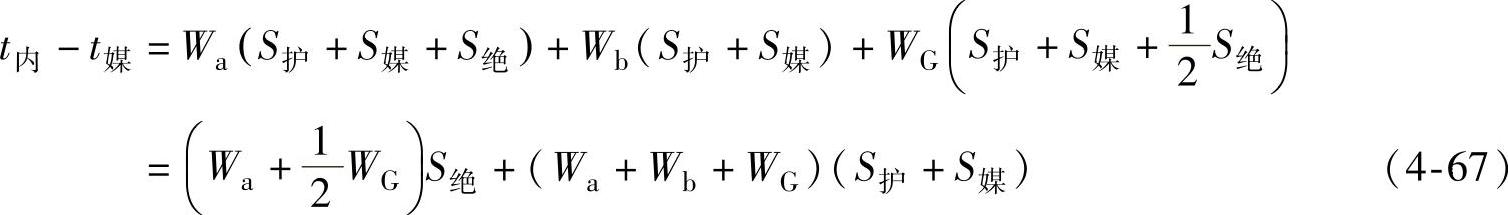
将式(4-59)代入式(4-64),则得电缆热平衡基本方程式
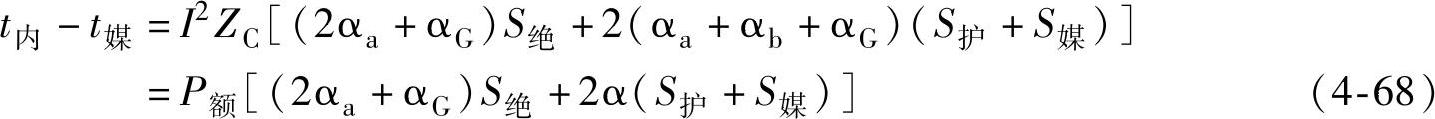
由此可得沿电缆传输的额定平均功率为
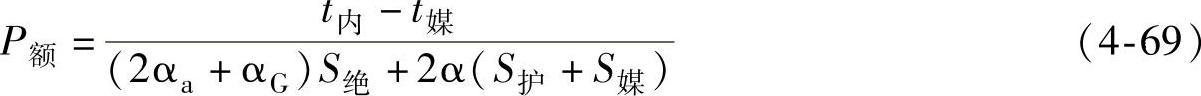
式中 t内——电缆中允许的最高温度(℃);
t媒——电缆周围媒质的温度(℃);
αa、αG、α——相应为内导体、绝缘层及电缆的衰减常数(奈/厘米);
S绝、S护、S媒——绝缘层、外护层及周围媒质的热阻(热欧·厘米)。
式中的衰减常数应取最高允许温度下的值。
由上式可见,电缆允许传输的最大功率为所选定电缆结构的容许最高使用温度的函数。
由式(4-69)计算所得的额定平均功率(记为P额)是在行波状态下,即负载匹配时求得的。实际上电缆往往是在失配情况下运行,失配将造成反射使损耗增加,因而允许传输的功率将减小。额定平均功率与驻波系数、调制度有如下关系:
在低频下

在高频下

式中 P额——未调制、行波下由式(4-69)计算出的额定平均功率;
m——调制度;
S——电压驻波系数。
在射频电缆中,承受高温作用的结构元件是绝缘。对于聚乙烯绝缘,最大允许温度为85℃,对于聚四氟乙烯绝缘为250℃。在对射频电缆进行热计算时,周围空气温度取为+40℃,因此电缆中的允许温度降为(t内-t媒),对于聚乙烯是45℃,对于聚四氟乙烯是205℃。可见,采用耐高温的绝缘材料,可大大提高额定平均功率值。
当环境温度变化时,额定平均功率也随之变化。在其他环境温度下的额定平均功率可由下式求出。

式中 t内——电缆最高允许温度(℃);
t——实际工作时的环境温度(℃);
t0——额定平均功率规定的环境温度,一般取+40℃;
P额——+40℃环境温度时的额定平均功率。
额定平均功率与电缆结构尺寸及频率的关系如图4-31所示。
由式(4-69)及图4-31可以看出,额定平均功率与电缆结构尺寸及传输频率有关。空气绝缘较实体绝缘有较低的衰减,因而传输的功率较大。随着电缆直径增加,则传输功率增加,而频率越高,电缆衰减越大,则传输的功率就越小。
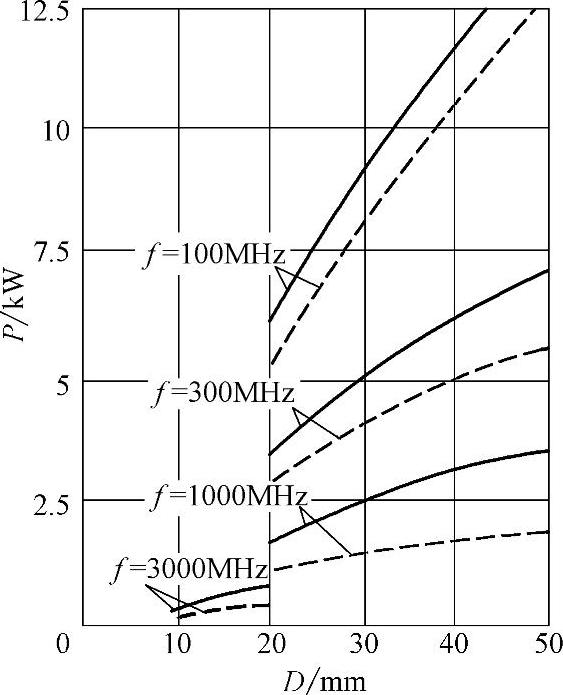
图4-31 额定平均功率与电缆结构尺寸及频率的关系
实线表示当ε=1.4时,聚乙烯空气绝缘;
虚线表示当ε=2.28时,实体聚乙烯绝缘。
此外,额定平均功率也会随着一些环境因素变化而变化。如当电缆使用在高空时,随着离地高度的增加,空气越稀薄,表面散热将越加困难,额定平均功率也就随之而下降。
上述公式只适用于实体绝缘射频电缆额定平均功率的计算。对于空气绝缘电缆,绝缘层中的热流要通过传导、对流、辐射三种形式散热,这与实体绝缘电缆不同,而其热阻的计算也与实体绝缘电缆不同,因此不能用上述公式计算空气绝缘电缆的额定平均功率。对于空气绝缘电缆的额定平均功率的计算,应用图解法来求,但计算的基本方法基本类似。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




