电缆衰减与导体材质与形式的关系

在射频下，同轴电缆的衰减通常可用下式来表示

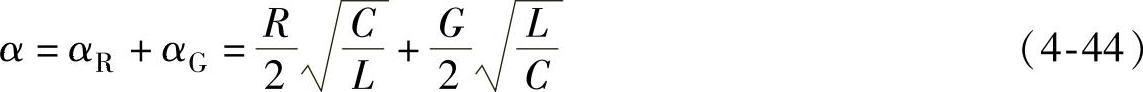
1.内、外导体为理想圆柱体时

同轴射频电缆的内、外导体都是由铜制成的圆柱形导体时，其衰减（N／km）可按下式进行计算

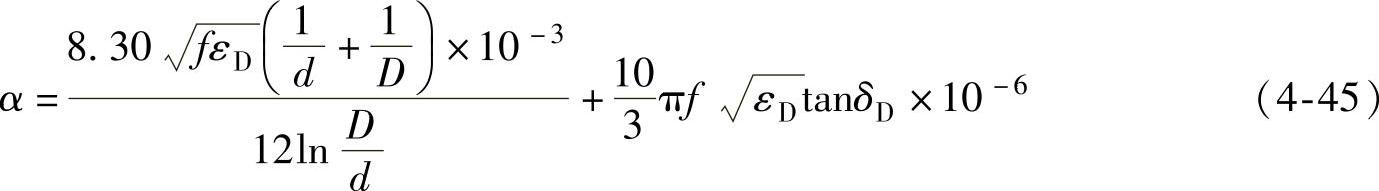
如将上式中自然对数化为常用对数，并且衰减常数以dB／m来表示，上式将变为

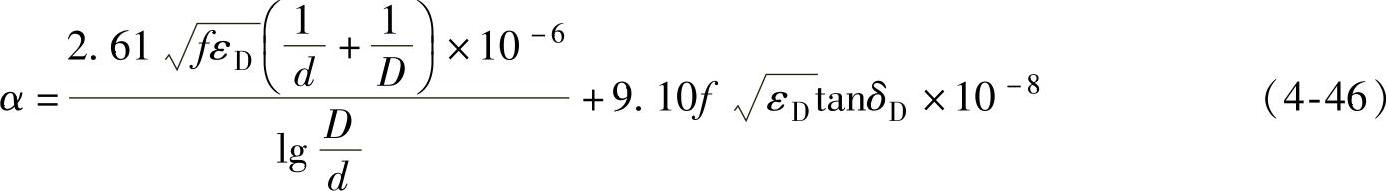
式中 D——外导体内径（mm）；

d——内导体直径（mm）；

ε_D——绝缘的等效相对介电常数；

tanδ_D——绝缘的等效相对介质损耗角正切值；

f——频率（Hz）。

2.当内导体为绞合内导体，外导体为编织时，并且内、外导体的电阻率分别为ρ₁和ρ2，则衰减（dB／m）公式

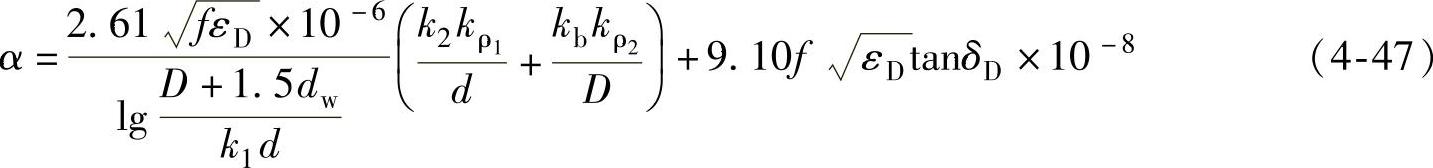
式中 k₁——内导体有效直径系数（见表4-4）；

k₂——内导体衰减的绞线系数（见表4-4）；

k_b——外导体为编织时引起射频电阻增大的编织效应系数（见图4-25）；

kρ₁——内导体相对于国际标准软铜的射频电阻增大或减小的系数；

kρ₂——外导体相对于国际标准软铜的射频电阻增大或减小的系数；

d_w——编织用导线直径（mm）。

图4-25 编织效应系数k_b与电缆绝缘外径的关系曲线

内导体衰减的绞线系数k₂表示直径为d的绞线导体的衰减比直径为d的实体导体衰减大的倍数。

编织效应系数k_b表示外导体采用编织时，外导体的衰减与相应直径理想圆管外导体的衰减之比值。图4-25所示为编织效应系数k_b与电缆绝缘外径D的关系曲线，它适合在700兆赫以下的频率范围内使用。在更高的频率时，k_b值将比图示值大1.2～1.5倍。因编织线间存在有接触电阻，在频率增高时，此接触电阻也参与导电，并且随频率的增高，通过接触电阻的电流将增加，甚至完全通过接触电阻来导电，而接触电阻很大，因此在频率很高时，相当于外导体电阻增加，k_b值也相应地增加。接触电阻与线表面情况、接触压力有关，还会随着电缆的弯曲以及使用过程中的老化而变化，因而将使电缆的衰减增大而且不稳定。

当内、外导体不是标准软铜，而是其他金属材料时，其衰减增大或减小的系数kρ值及相应材料的电阻率见表4-5。

表4-5 常用金属材料的电阻率及系数kρ(www.xing528.com)

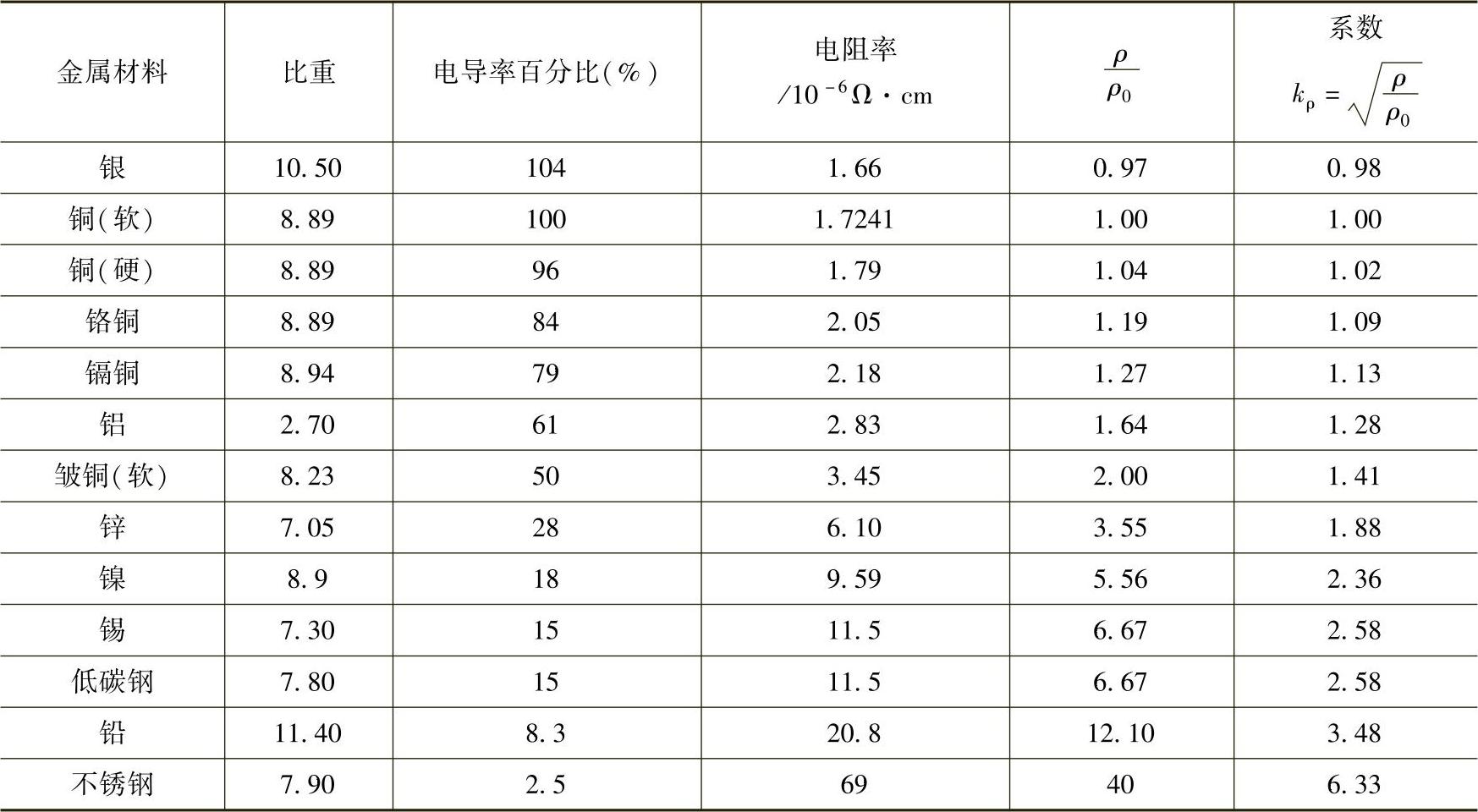
注：ρ₀为国际标准软铜的电阻率，ρ₀＝1.7241×10^-6Ω·cm。

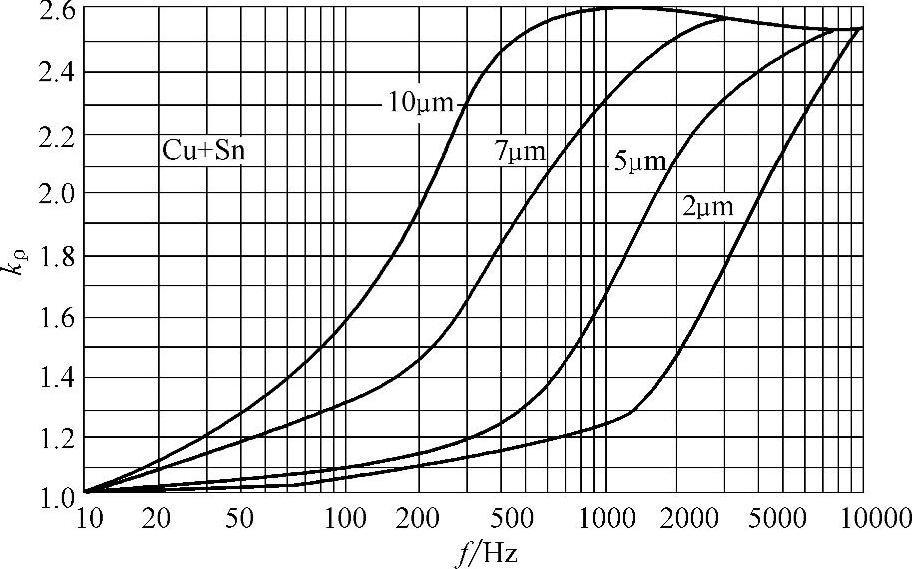
图4-26 镀锡铜线kρ与频率的关系曲线

如果导体采用镀银铜线、镀锡铜线或铜包钢线等双金属结构形式与采用铜线相比，衰减的改变也可用系数kρ来表示。kρ值的大小与镀层的厚薄及使用频率有关。在很高的射频下，可以把它看成由表面层材料构成的单金属导体来处理。但是，当表面层极薄，或使用频率较低时，表面层和内部金属层都参与导电作用。此时双金属导体的衰减与表面层金属材料及厚度、内部金属材料以及使用频率都有关。图4-26、图4-27给出镀锡铜线、镀银铜线的系数kρ与频率的关系曲线。

图4-27 镀银铜线kρ与频率的关系曲线

由图4-26及图4-27可见，镀锡铜线适于较低频段，而镀银铜线适于较高频段。

3.当内导体为铜绞线，外导体为扁铜线绞合时，衰减的计算公式为

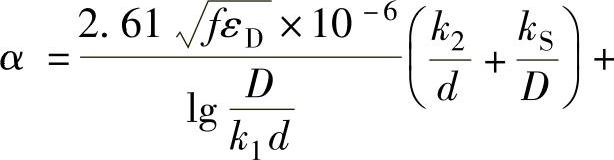
式中 k_S——扁线绞合结构引起电阻增大的系数，一般可取1.07～1.10。

4.当内、外导体为皱纹管结构时，衰减计算公式为

式中 d_e——皱纹管内导体的等效直径，d_e＝d₀-δ₁；

D_e——皱纹管外导体的等效直径，D_e＝D_i+δ₂；

d₀——皱纹管内导体的外径（mm）；

D_i——皱纹管外导体的内径（mm）；

δ₁——皱纹管内导体的轧纹深度（mm）；

δ₂——皱纹管外导体的轧纹深度（mm）；

k_e1、k_e2——分别为皱纹管内、外导体与光管相比，其高频电阻增大的系数。对于皱纹铜管

k_e1（或k_e2）＝1.15～1.20，对于皱纹铝管k_e1（或k_e2）＝1.47～1.54。

上面讨论的衰减计算公式都是在常温下的公式，在大功率射频电缆中，内、外导体的温度会升高，环境温度也要变化，因此导体电阻会随之改变，从而使衰减随之而变。要引入一个衰减温度系数，以反映电缆衰减随温度的变化情况。

上述各公式所计算的衰减都是认为电缆本身是均匀的，但电缆在实际的工作状态下，电缆本身可能不均匀，负载也可能不匹配，因而存在驻波，它会使电缆线路的总衰减增大。