对称电缆电感特性分析

当回路通以交流电后，则在回路的导电线芯中和回路周围产生磁通ϕ，在导电线芯内的称为内磁通，在导电线芯外的称为外磁通。二电感为磁通ϕ与引起磁通的电流之比，所以相应于内磁通与外磁通亦有内电感L_内和外电感L_外，总电感为L＝L_内+L_外。

内电感L_内是由导线内部的磁通与流过导线的电流之比所决定的。导线内磁通的大小与导线内的电流分布有关，因此内电感L_内与导线内的电流分布有关。内电感的计算公式可在求二孤立导线有效电阻时，求其复数功率的虚部来求得。其计算公式如下：

L_内＝Q（x）×10^-4（H／km） （3-8）

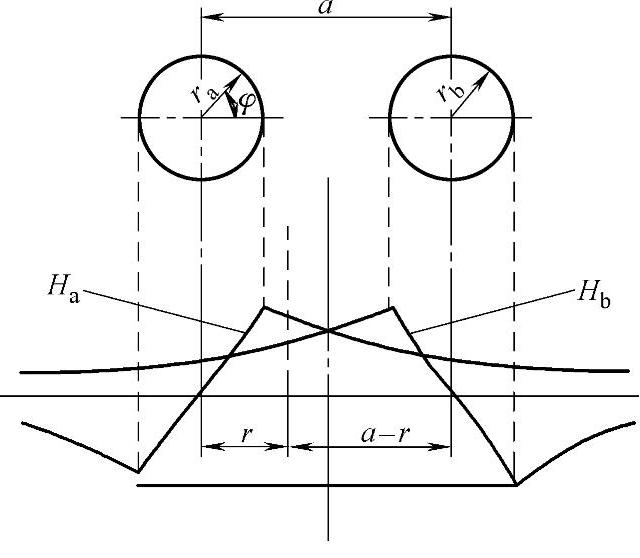
图3-17 对称回路的磁场分布

外电感L_外是导线外（与回路本身所交链的）磁通与流过被交链导线中的电流之比，即L_外＝ϕ／I。

对称回路的磁场分布如图3-17所示。

回路两导线中，由导线a中电流所产生的磁场强度为

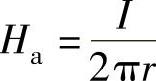
由导线b中电流所产生的磁场强度为

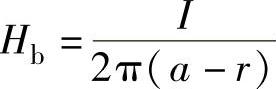
从图3-17可以看出

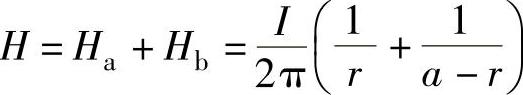
因此，外电感H_外 可由下式求得

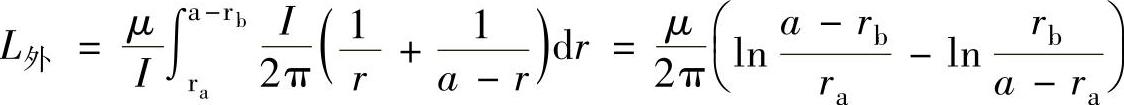
回路两导线r_a＝r_b＝d／2，则

回路中间为非磁性介质，μ＝μ_rμ₀＝4π×10^-7（H／m），则

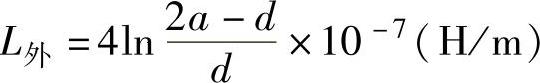
或

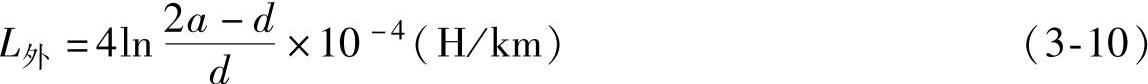
由此可得对称电缆回路的总电感（H／km）(www.xing528.com)

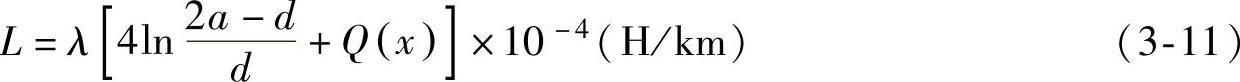
式中 λ——总的绞合系数；

a——回路两导线中心间距（mm）；

d——导电线芯直径（mm）；

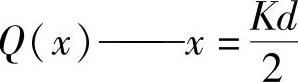的特定函数，其值见表3-18。

由式（3-11）可见，外电感决定于导电线芯直径和导电线芯间的距离。内电感决定于导电线芯本身的特性（导线直径、材料的磁导率和电导率）和传输电流的频率。

图3-18所示为线间距离改变时，电感与线间距离的关系。随导线间距离a的增加，回路所交链磁力线的面积增加，因而外磁通增加，外电感亦随之增加。正因为这样，架空明线的电感较电缆的电感大两倍多。

随着导电线芯直径d的增加，趋肤效应增强，导线中的磁通减小，因而内电感减小。同时，由于外磁通所穿过的面积减小，外电感就下降，因此回路总电感随导电线芯直径的增加而减小，对称回路的电感与导电线芯直径的关系如图3-19所示。

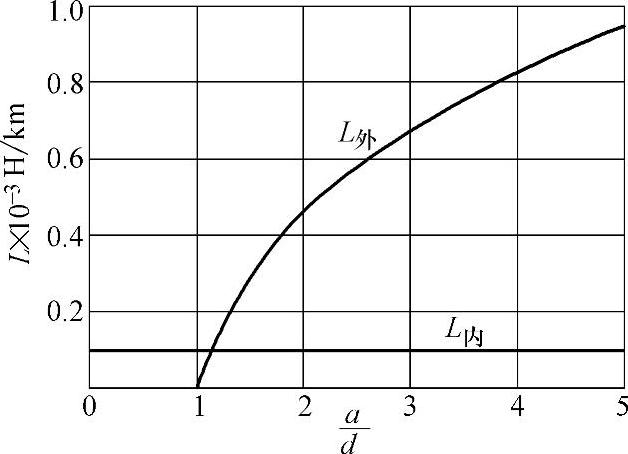
图3-18 电感与线间距离的关系

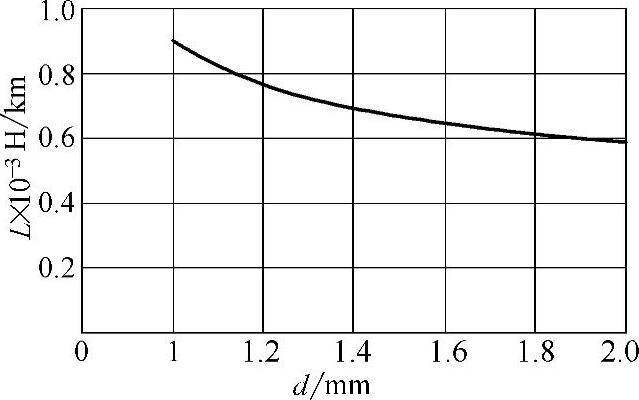
图3-19 对称回路的电感与导电线芯直径的关系

随传输电流频率的增加，回路的总电感将减小。这是由于频率增加时，趋肤效应增强，使内电感减小，而外电感与频率无关，所以随频率的增加，总电感近似于外电感。

对称屏蔽回路的电感，除了内电感L_内和外电感L_外之外，还有屏蔽体给传输回路带来的附加电感。从理论上说，邻近作用使电感减小，但其值很小，可以略而不计。

对称屏蔽回路总电感为

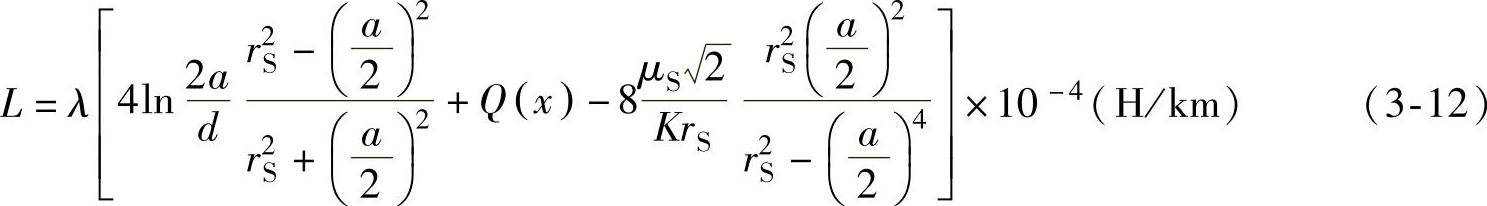
式中r_S——屏蔽层的内直径（mm）；

μS——屏蔽层的相对磁导率；

K——涡流系数，见表3-17。

由于屏蔽的作用，回路的外电感减小。这是因为屏蔽层产生了与基本场相反的反射场，其相互作用的结果，使回路间的合成磁场减弱，因而使回路的电感也随之减小。

从式（3-12）可见，如没有屏蔽层，则认为r_S趋于无穷大，则式（3-12）就与式（3-11）一致了。