对称电缆的有效电阻计算方法

所谓有效电阻就是当交变电流流过对称回路时的电阻，包括直流电阻R₀和由通过交流而引起的附加电阻R～，即

R＝R₀+R～

对于5000Hz以下使用的低频电缆，电缆回路的有效电阻近似等于回路的直流电阻。如市内通信电缆（用于音频传输）回路的有效电阻就几乎等于回路的直流电阻。对于高频对称电缆，电缆回路的有效电阻就不能用直流电阻来代替，因为这时交流附加电阻R～与有效电阻R相比将占很大比例，因而不能忽略。

1.回路直流电阻的计算

回路直流电阻就是电缆中一个回路接成环路时的直流电阻，根据电工基础概念并考虑绞合因素，其计算公式如下：

式中 ρ——导电线芯的电阻率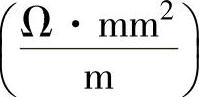，见表3-14；

λ——导电线芯的总绞合系数，导电线芯每次绞合的绞合系数见表3-15，总绞合系数为各次绞合时绞合系数的乘积；

l——电缆的长度（m）；

S——导电线芯的截面积（mm²）。

如果将导电线芯的截面积S以导电线芯直径d表示，并且换算为每公里的电阻值（Ω／km），则式（3-1）变为

式中 d——导电线芯直径（mm）。

由式（3-2）可见，直流电阻主要与导电线芯材料的电阻率ρ和直径d有关。

表3-14中电阻率ρ值是温度为20℃时的值。当温度不等于20℃而为任一温度t℃时，则电缆回路的电阻R可以用下式进行换算：

R_t＝R₂₀[1+α₂₀（t-20）] （3-3）

式中 R₂₀——温度为20℃时的导线电阻；

α₂₀——电阻温度系数（20℃），见表3-14。

表3-14 通信电缆用主要金属材料的特性

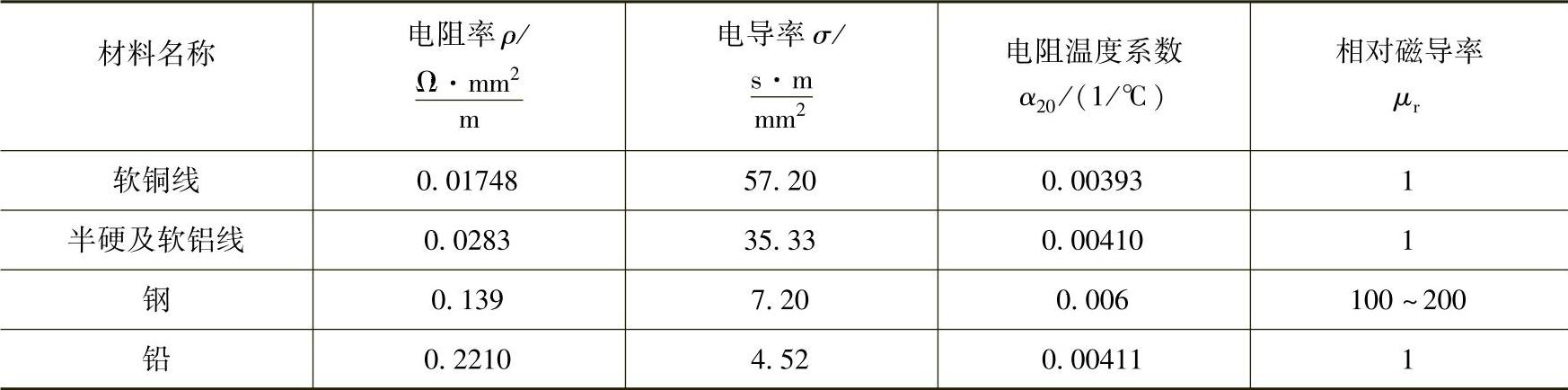
表3-15 线芯绞合的绞合系数

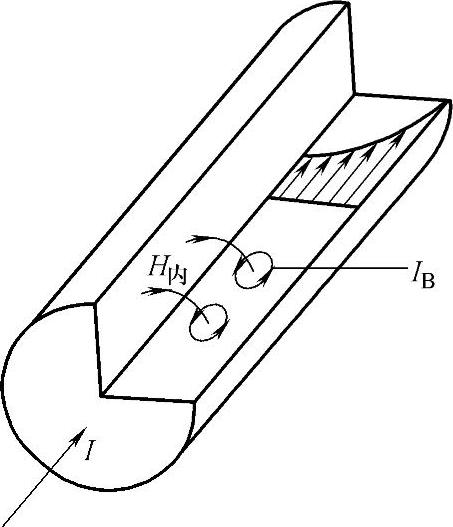
图3-15 趋肤效应

2.交流附加电阻的物理概念和组成

在回路中通以交变电流后，所引起的附加电阻是由于趋肤效应、邻近效应和在周围金属媒质中产生的涡流损耗三部分所引起的。因为通交流电后，在导体内部和周围将产生磁场，由于交变磁场作用于导体，并因此而引起能量损耗，从本质上可以认为是电阻的增加。这样，所增加的电阻就称为交流附加电阻。附加电阻可以分为下列三种。

（1）由趋肤效应引起的附加电阻

趋肤效应是由沿导线内产生的涡流造成的。如图3-15所示，当交流电通过导线时，则在导线内部产生交变磁场H_内，变化的内磁场的磁力线穿过导线内部时，在导线内部就感应出涡流I_B。涡流I_B的方向根据楞次定律来确定。在导线的中心，涡流的方向与基本电流的方向相反，合成电流为I-I_B；而在导线表面，涡流I_B与基本电流I的方向相同，合成电流为I+I_B；结果使得导线横截面上的电流重新分布，导线表面的电流密度增大，而导线内部电流密度减小。这种由于本导线内的涡流把基本电流挤到表面上的现象称为趋肤效应。趋肤效应与电流的频率、导线的电导率、磁导率及直径有关。电流频率越高，趋肤效应就越显著，电流几乎仅通过导线的表面，这就相当于导线通电流的截面积减小，因而使回路的有效电阻增加。这部分因趋肤效应而增加的电阻用R_趋表示。

（2）由邻近效应所引起的附加电阻

邻近效应是回路中一根导线通过的电流在另一根导线中产生的涡流造成的。如图3-16所示，回路中的“导线1”通过交流时，它的外磁场H_外在“导线2”上引起涡流I_B，这一涡流与“导线2”上的基本电流相互作用后，在“导线2”靠近“导线1”的一面，涡流I_B与基本电流I的方向相同（I+I_B），而在远离“导线1”的一面则方向相反（I-I_B）。同样，在“导线1”中也发生电流重新分配的情况。涡流和基本电流相互作用的结果，使得在“导线1”和“导线2”彼此对着的一面电流密度增加，而在远离的一面电流则减小，

这种现象称为邻近效应。邻近效应除与电流频率、导线的电导率、磁导率及导线直径有关外，还与两导线的距离有关。当存在邻近效应时，电流都趋向两导线相邻的一侧，这样也使通电流的有效截面积减小，从而使回路的有效电阻增加。这部分由邻近效应增加的电阻用R_邻表示。

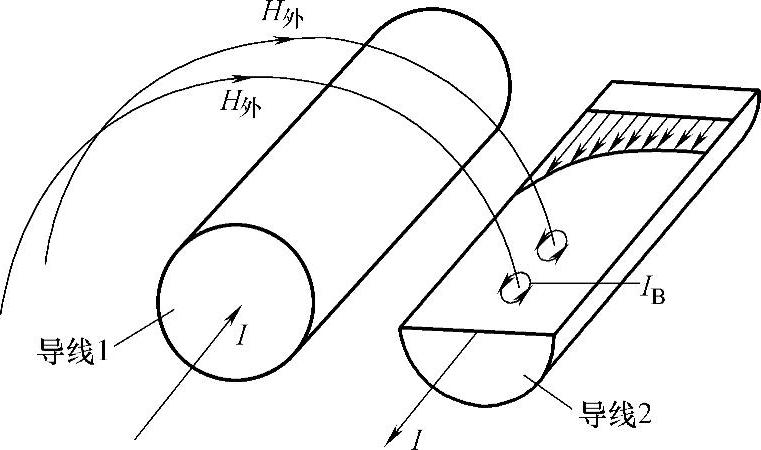
图3-16 邻近效应

（3）由邻近金属损耗所引起的附加电阻

回路电流的外磁场会在邻近的导线中、周围的屏蔽层中、金属套及铠装等金属中引起涡流。此涡流使邻近金属变热并产生能量损耗，这种损耗势必吸引传输回路中的一部分能量，因此，可以看成在传输回路上有一个附加电阻R_金。(www.xing528.com)

综上所述，回路的有效电阻R是由R₀、R_趋、R_邻和R_金组成，即

R＝R₀+R～＝R₀+R_趋+R_邻+R_金 （3-4）

有效电阻的四个部分中，前三部分可以利用电磁场理论进行计算，而对R_金的计算则非常困难，一般是用实验的方法或利用经验公式来确定。

3.二孤立导线有效电阻的计算

所谓二孤立导线，是指在无穷大的空间内，只有一个回路的两根导线，而周围没有其他回路和金属层。在这种情况下，在有效电阻的计算公式中，就不包括R_金部分，而剩下R₀、R_趋和R_邻三部分。对于R_趋和R_邻的大小取决于导线界面上电流分布的不均匀程度，而电流分布的不均匀程度是很难确定的，因此我们求取有效电阻的方法是根据能量守恒定律。

当导线通以交流电后，它将遇到由导线的有效电阻R和内电感L_内所组成的阻抗Z＝R+jωL_内，所产生的能量损耗，用功率P表示为

P＝I²Z＝I²R+jI²ωL_内（3-5）

功率的实部表示有功功率，虚部表示无功功率。根据能量守恒定律，这部分功率是由外界所供给的，就是说有一部分大小相等的功率流入导线内部。如果能把流入导线内部的功率求出，根据其实部可求得有效电阻，根据其虚部可求得内电感。

由电磁场理论来求二孤立导线所构成的回路有效电阻（Ω／km）的计算公式为

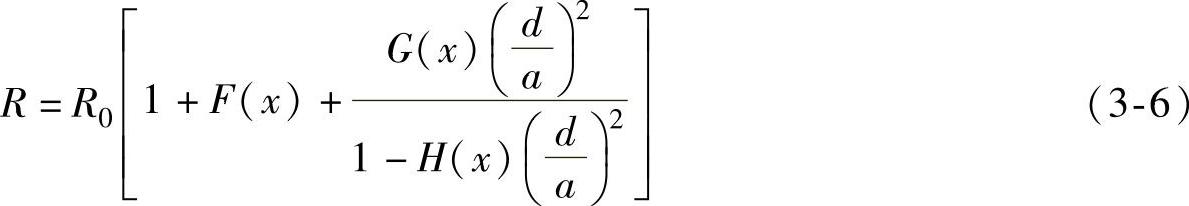
从前面分析可知，二孤立导线的有效电阻应该包括三项，即R＝R₀+R_趋+R_邻，在式（3-6）中也包括三项，我们来分析一下每一项是否符合上述的推论。

式中 R₀——回路的直流电阻；

R₀F（x）——由趋肤效应引起的附加电阻，其中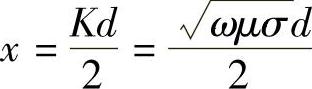，即这部分电阻与导线直径、信号频率、导线的磁导率和电阻率四个参数有关，所以我们判定它是由趋肤效应引起的附加电阻R_趋。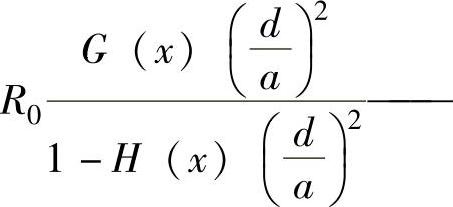由邻近效应引起的附加电阻。因为它除了与导线直径、信号频率、导线的磁导率和电阻率四个参数有关外，还与回路二导线间距离有关，所以我们判定它是由邻近效应引起的附加电阻R_邻。

4.对称电缆回路有效电阻的计算

式（3-6）可精确地计算出孤立对绞组的有效电阻。但对于星绞组和复双绞组，就很难给出精确的结果。因为在星绞组和复双绞组中除计算回路外，还有另一个回路存在。当线组中存在另一回路时，对邻近效应有影响，此时相应于附近附加电阻有所增加，这可在式（3-6）引入修正系数p来考虑。各种四线组修正系数p值见表3-16。

表3-16 各种四线组的修正系数p值

一般对称电缆中有若干个线组或金属套，所以还要计算在其他线组及金属套中的涡流损耗而引起的附加电阻R_金。

由此，对称电缆回路有效电阻的完全计算公式为

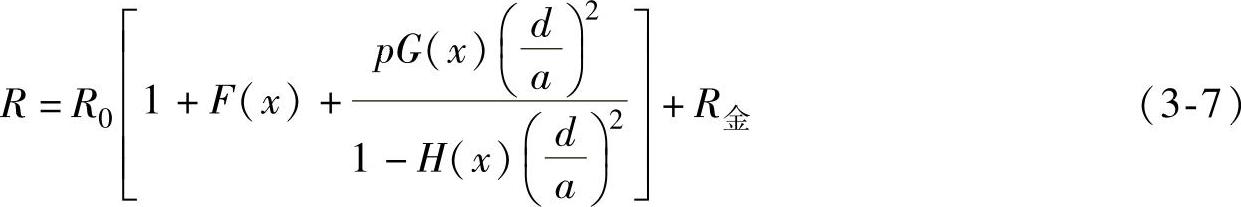
式中 R₀——回路直流电阻（Ω／km）；

d——导电线芯直径（mm）；

a——回路两导线中心间距离（mm）；

p——各种四线组的修正系数，见表3-16；

x——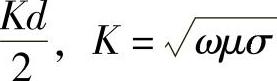为涡流系数，见表3-17；

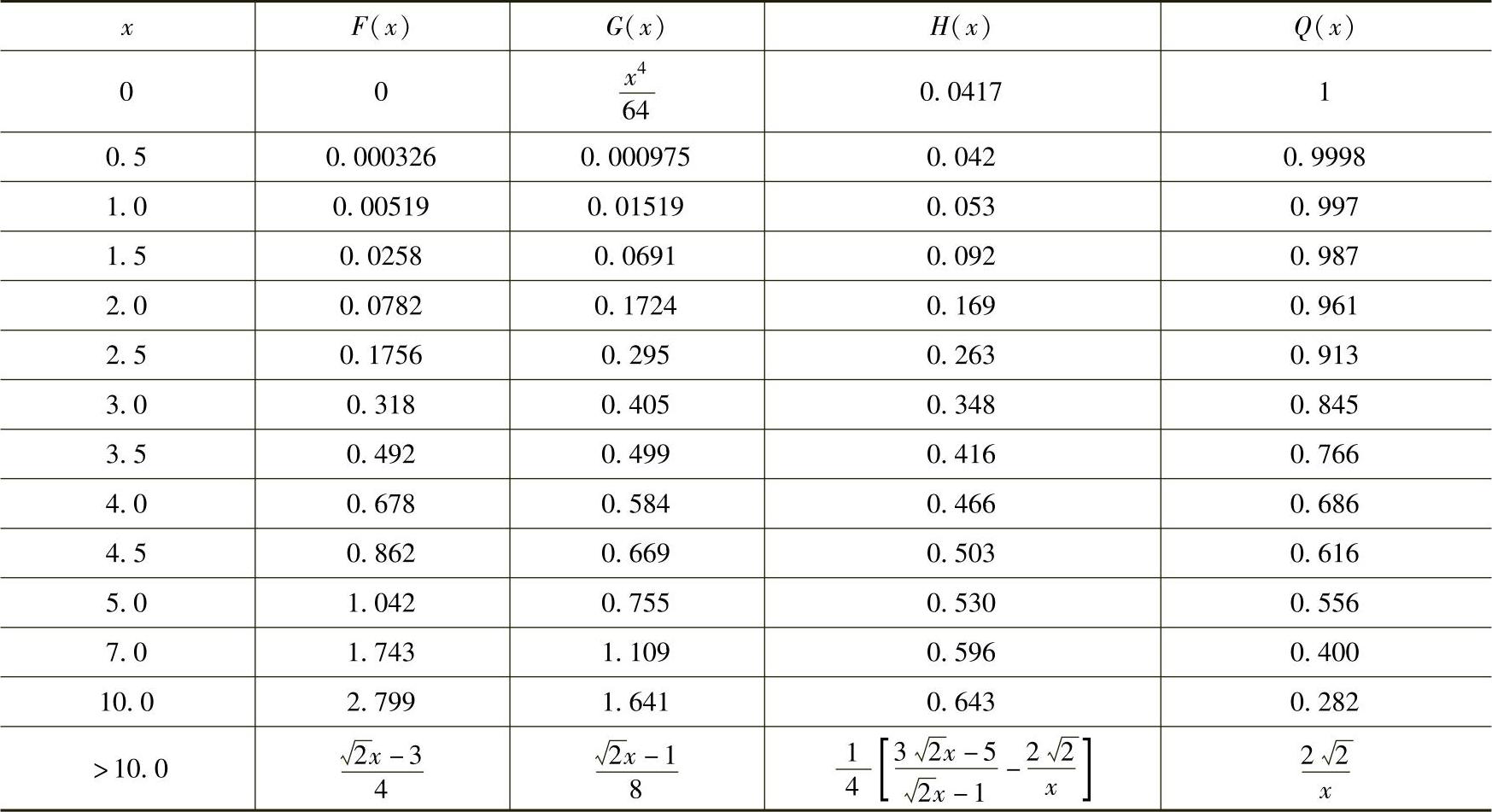
F（x）、G（x）、H（x）——x的特定函数，其值见表3-18。

式（3-7）中的R_金是计算在回路外的其他回路及金属套中的涡流损耗引起的附加电阻。因为回路周围的电磁场分布是非常复杂的，所以对附加电阻R_金不可能进行精确地计算，一般是用实验方法来确定。

表3-17 各种常用金属的涡流系数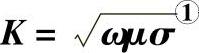

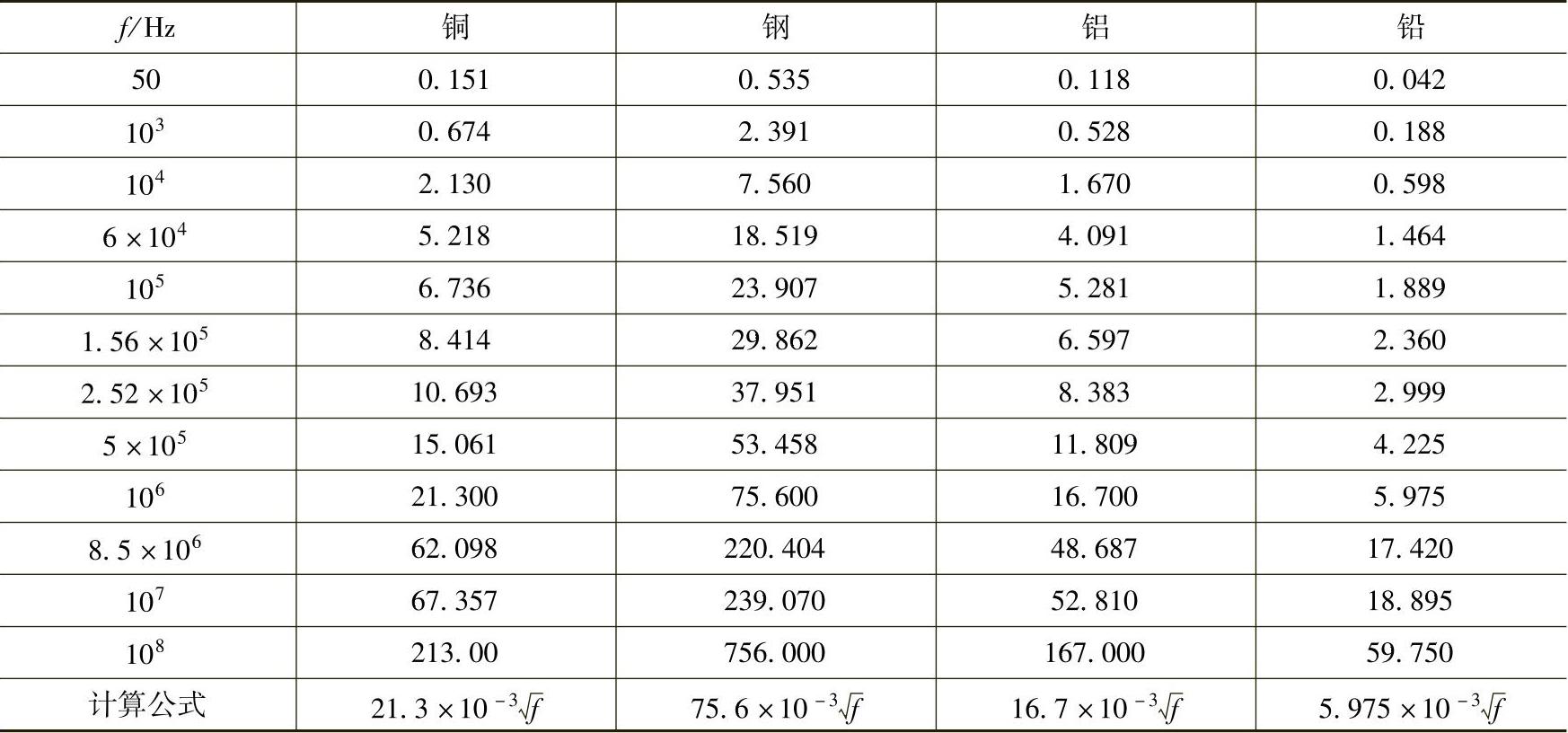
①_μ为磁导率，μ＝4π×10^-7μ_r（H／m），μ_r见表3-14，计算钢的涡流系数时，取μ_r＝100。

σ为电导率，见表3-14。

表3-18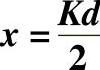不同时函数F、G、H和Q的数值