传播常数计算公式详解

由式（2-5）可知，传播常数γ为

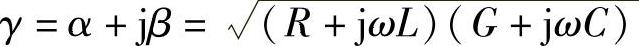
将上式右边等号的两边平方，得

α²+j2αβ-β²＝（RG-ω²LC）+jω（RC+LG）

上式等号两边实部与虚部分别相等，得

α²-β²＝RG-ω²LC

2αχ＝ω（RC+LG）

上两式联立，解得

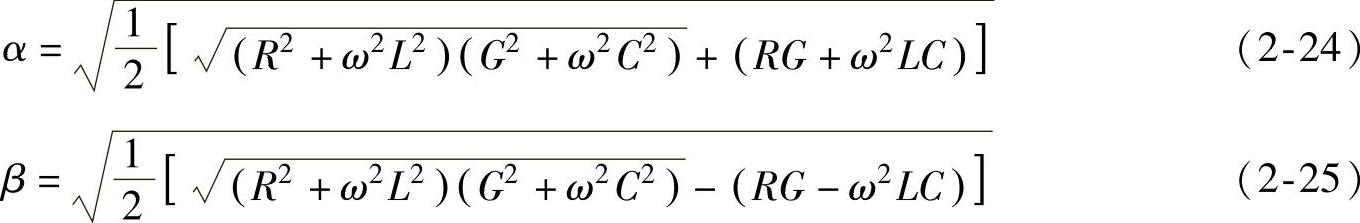
式（2-24）及式（2-25）和波阻抗的计算公式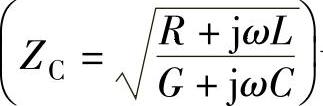一样，可以对各种双线回路当频率从零至无穷大时进行计算，但公式较为复杂。下面讨论在不同频率范围内，衰减常数α和相移常数β的简化计算公式。

1.在直流时（f＝0）

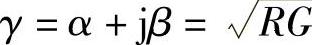
因而

2.在音频时（f≤800Hz）

在此频率范围内，R≫ωL、G≪ωC，可略去ωL和G，则

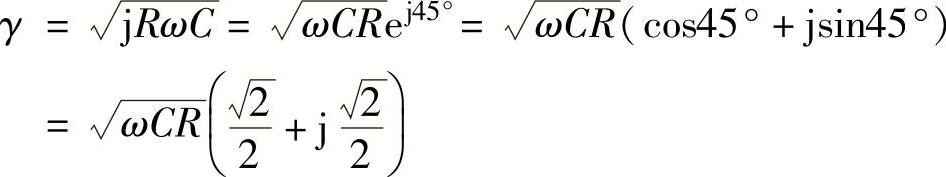
故

3.在高频时（f＞30kHz）

为了简化公式，可把γ全式改写成

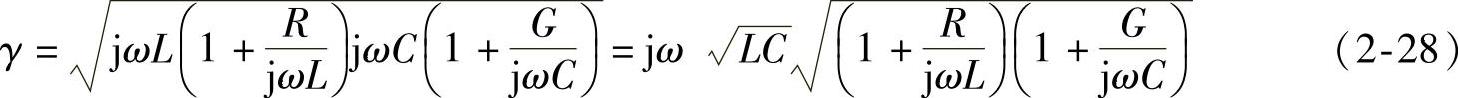(https://www.xing528.com)

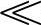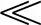因为在高频时，RωL、GωC，所以

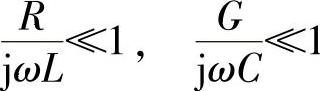
根据级数展开

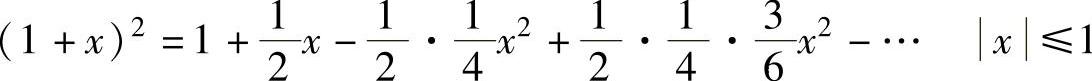
把高次项舍去，则

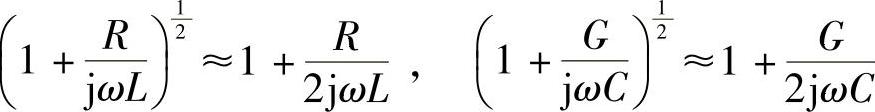
将此值代入式（2-28）并整理得

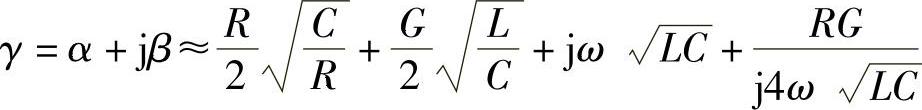
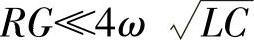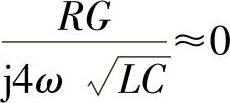高频时，，所以，因此得

大约从30kHz起，按式（2-29）、式（2-30）对电缆线路进行计算，就具有足够的准确性。例如在对称的通信电缆中，当频率为20kHz时，衰减常数α的误差不大于3％，而相移常数β的误差不大于1％，伴随频率的增高，这些简单公式的误差将下降。

当频率在800～30000Hz范围内，采用完全公式计算。

表2-1中列出了在不同频率下二次传输参数的计算公式。

表2-1 二次传输参数在不同频率下的计算公式

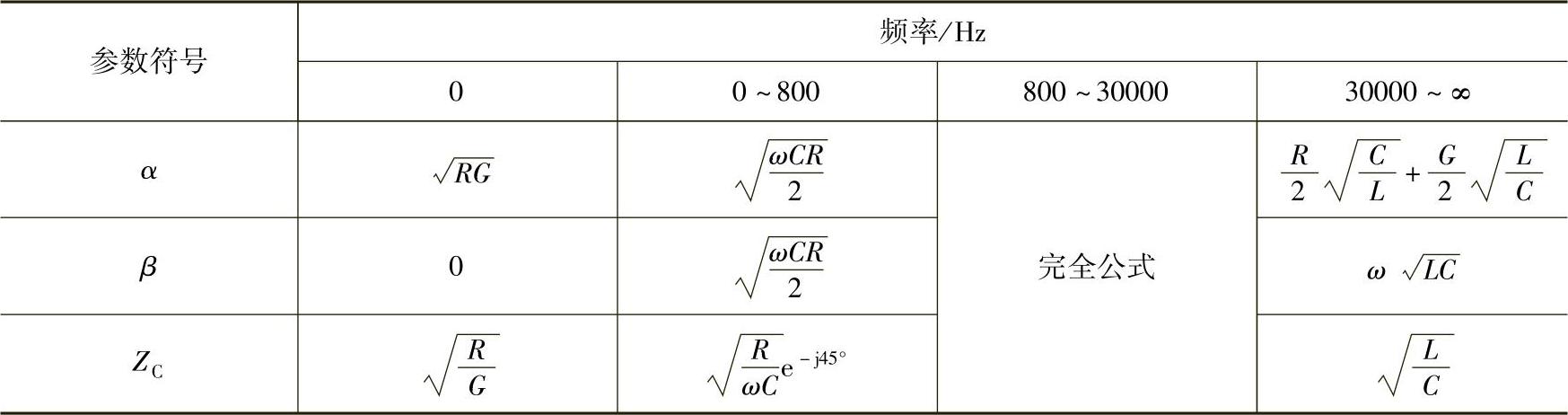
图2-4所示为电缆线路的衰减常数和相移常数与频率的关系。从前面的分析及图2-4中曲线可知，在直流时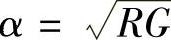，当频率开始增加后，按规律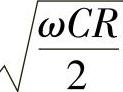迅速增大，而后增大的速度又缓慢下来。相移常数β从零开始（当f＝0）随频率的增加在音频时与衰减常值相等，然后在高频范围内按照公式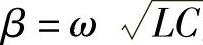所确定的直线规律增长。

由图2-4中α-f曲线可见，在曲线中出现一个很弯曲的线段，对于直径d＝1.2mm的对称通信电缆，其α-f曲线在12kHz以下弯曲较大，在12kHz以上的曲线接近于直线。另外由图2-3可知，对称通信电缆的波阻抗Z_C在12kHz以上变化缓慢，因此高频对称通信电缆载波通信的起始频率都从12kHz开始，这对载波机的阻抗匹配和衰减均衡都是有利的。

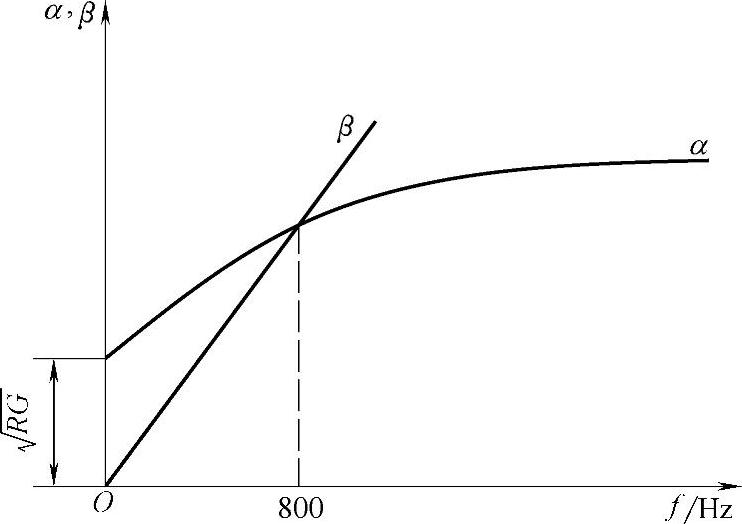
图2-4 电缆线路的衰减常数和相移常数与频率的关系