均匀电缆传输的基本方程

为了研究无限短长度（dx）电缆段上电压和电流的变化规律，以及电压和电流的关系，可利用图2-1所示的均匀电缆的等效回路来求得。当所加电压和电流为正弦波时，在dx段内有Rdx、Ldx、Cdx、Gdx。串联阻抗Zdx＝（R+jωL）dx，并联导纳Ydx＝（G+jωL）dx，在dx小段起点处，电压为U，电流为I；在dx小段终点处，电压为U+dU，电流为I+dI。

根据基尔霍夫第一、二定律，可列以下方程：

U（U+dU）＝I（R+jωL）dx

I（I+dI）＝（U+dU）（G+jωC）dx （2-1）

对式（2-1）进行整理，并忽略（G+jωC）dxdU，可以得到下列微分方程：

上式左边的微分方程取负号表明电压和电流随x增加而减小。

如果将式（2-2）对x偏微分，并将式（2-2）中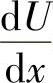和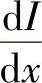的值代入可得

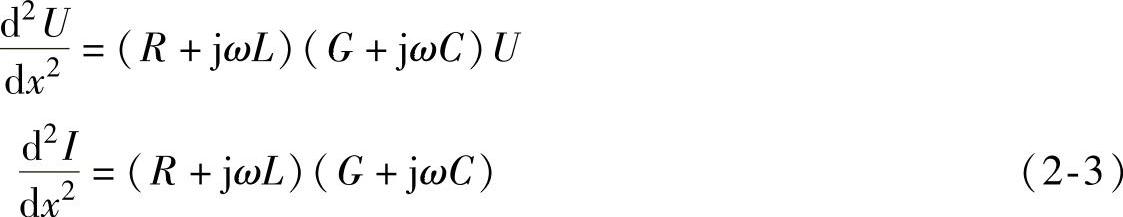
令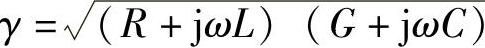，则式（2-3）可写成

在式（2-4）中，U的通解为

U＝A₁e^-γx+A₂e^γx （2-5）

由式（2-2）中第一式可得

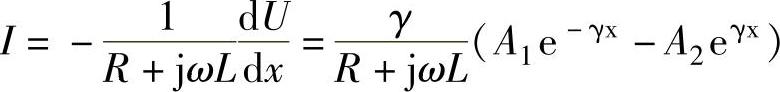
令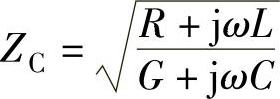，则

如果已知电缆始端（即x＝0处）的电压为U₀和电流为I₀，代入式（2-5）及式（2-6），

可确定出积分常数A₁和A₂。

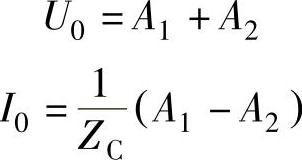
解上式可得(https://www.xing528.com)

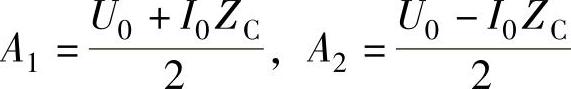
将A₁及A₂代入式（2-5）及式（2-6），可获得用始端电压和电流来表征通信线路沿线电压和电流分布的公式，即

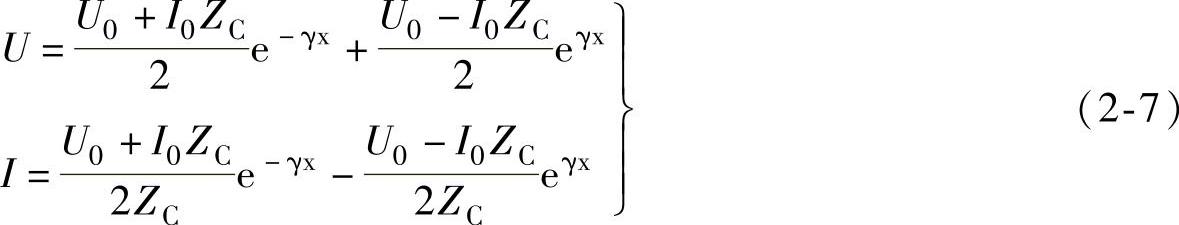
如果电缆线路长度为l，则其终端的电压和电流值可通过式（2-7）变为

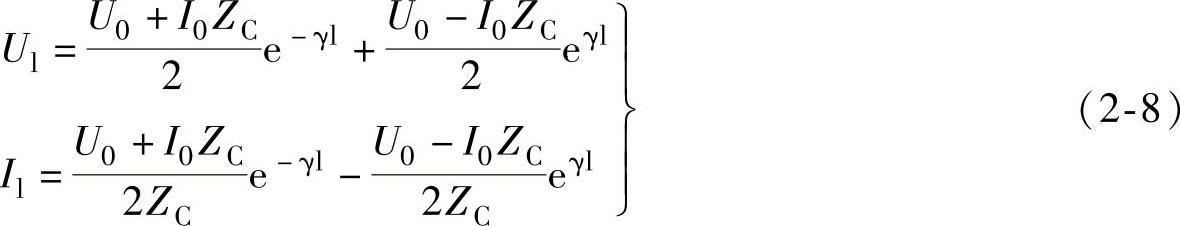
式（2-8）也可用双曲函数表示：

式（2-7）及式（2-8）中的x，l是从线路始端算起的。

若已知线路终端电压U_l和电流I_l，且线路长度是从终端算起的，则始端的电压U₀和电流I₀可由下式求取。

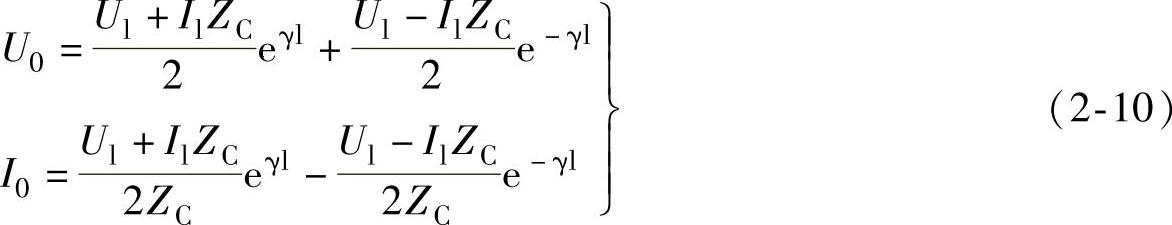
式（2-10）也可用双曲函数表示：

式（2-11）称为均匀传输线路的基本方程。

式（2-6）～式（2-11）中的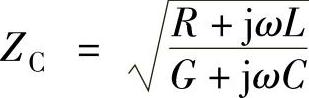称为波阻抗或特性阻抗，γ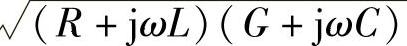＝称为传播常数。Z_C和γ与传输线的一次传输参数（R、L、C、G）有关，是用以表征传输线路特性的参数，称为传输线的二次传输参数。

正如声波和光波传输时具有反射作用一样，电磁波在不均匀线路（如电缆线路本身不均匀或线路的终端不匹配）上传输时，也会发生能量的反射。从式（2-7）可以看出，在x点（即线路上任意点）的电压和电流都是两个分量之和，其中一个分量随x增加而减小，另一个分量却随x增加而增加。很明显，具有负γ值的一项就是入射的电压波或电流波，而具有正γ值的另一项就是反射的电压波或电流波。在这种情况下，如用U_入、U_反、I_入、I_反分别表示入射及反射电压波及电流波，则式（2-7）变为

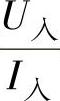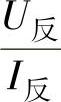如果取比例和就不难发现

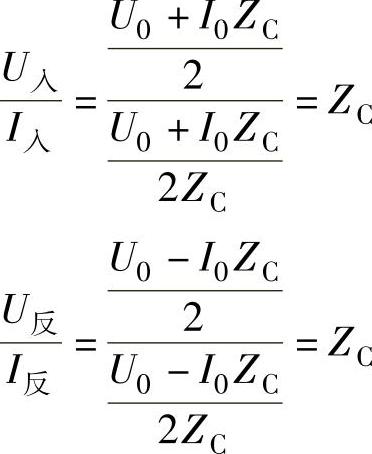
由此可知，入射电压波与入射电流波之比或反射电压波与反射电流波之比都是常数，并且都等于波阻抗Z_C。也就是说不论入射波还是反射波，在其传播中，在传输线的每一点上所遇到的都是数值为Z_C的阻抗，因而Z_C称为波阻抗。

从式中可以看出，γ这一数值表征电磁波沿线路传输时幅值和相位的变化程度，故称为传播常数，γ只与传输线路的一次参数及信号频率有关。