如果周期性时间函数F(t)的变化周期为T,频率f=1/T,一个周期T对应2π弧度(360°),那么F(t)=F(t+T)就是以周期为时间T表达的周期性时间函数,而F(ωt)=F(ωt+2π)就是以周期为2π弧度表达的相位角ωt的周期性相位角函数。式中角频率ωt=2πf=2π/T,ωt为以弧度为单位的相位角瞬时值。
周期性函数可以分解为无限项三角级数——傅里叶级数,即
在式(A-1)左、右两边取积分,可以求得式(A-1)中的C0、an、bn为
图A-2 单相桥双脉波相控整流电压波形
1.脉宽为θ的直流电压u(ωt)
图A-1所示的周期为2π,脉宽为θ的直流电压函数的特点是u(ωt)=u(-ωt)。这种对称的函数关系被称为偶函数或偶对称,利用图A-1的这种特性,由式(A-2)、式(A-3)、式(A-4)可求得u(ωt)的傅里叶级数表达式为
式(A-1)也可表达为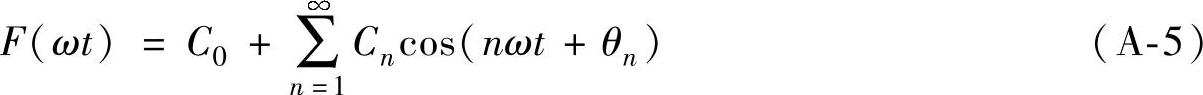
式中 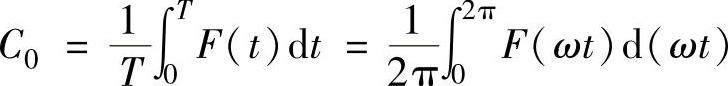
图A-3 脉宽为θ的单脉波交流电压波形
如果F(ωt)=F(-ωt),则称F(ωt)为偶函数或偶对称(Even Symmetry)。如图A-1所示。
如果F(ωt)=-F(-ωt),则称F(ωt)为奇函数或奇对称(Odd Symmetry)。
如果F(ωt)=-F(π+ωt),则称F(ωt)为半波对称函数或偶对称(Half-Wave Symmetry)。
图A-1 脉宽为θ的直流电压波形
电力电子变换系统中,F(t)是电流i(t)或电压u(t),因此其傅里叶级数表达式物理上是将周期性的电压、电流波形分解为直流分量C0以及基波C1(n=1时)和各次谐波分量Cn,Cn和θn分别是n次谐波的幅值和相角。n=1时,C1是基波幅值,θ1是基波相角。
实际应用中,为了改善开关型电力电子变换电路输出的负载电压波形u(t)和输入的电源电流波形i(t),常常安排开关器件的导通、阻断状态在时间上具有一定的对称性,从而在一个开关周期中使输出电压v(ωt)或输入电流i(t)在时间相位上具有一定的对称性。此外在分析电力电子变换电路的实际运行特性时,通常将开关器件视为理想开关,其开通过程(从通态到断态)和关断(从断态到通态)过程时间为零,只有导通和阻断两种工况,这也使电压、电流波形的数学表达式较简单,如图A-1、图A-2、图A-3等图中所示具有某些特定的对称性的直流电压,或交流电压片段,从而使其傅里叶级数表达式中某些项系数为零,且其他项系数的计算也变得比较简单。物理上这种情况就是这时电流和电压波形中不存在某些电压分量或电流分量。
以下给出实际电力电子变换中应用较多的几种电压(电流)波形及按以上各计算公式所得到的电压(电流)傅里叶表达式。
图A-2 单相桥双脉波相控整流电压波形
1.脉宽为θ的直流电压u(ωt)
图A-1所示的周期为2π,脉宽为θ的直流电压函数的特点是u(ωt)=u(-ωt)。这种对称的函数关系被称为偶函数或偶对称,利用图A-1的这种特性,由式(A-2)、式(A-3)、式(A-4)可求得u(ωt)的傅里叶级数表达式为
图A-3 脉宽为θ的单脉波交流电压波形
因此,偶对称或偶函数除直流分量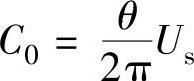 ,仅含1、3、5等次交流谐波。
,仅含1、3、5等次交流谐波。
2.单相桥双脉波相控整流电压u(ωt)
因此,偶对称或偶函数除直流分量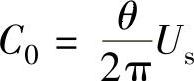 ,仅含1、3、5等次交流谐波。
,仅含1、3、5等次交流谐波。
2.单相桥双脉波相控整流电压u(ωt)
图A-2给出了单相桥双脉波整流电路负载电流iD连续时相控角为α整流输出电压uD的波形。从ωt=0开始的第1个脉波的电压uD为OPEFGQMH,在一个交流电源周期T(2π)中,有2个形状相同但相位差2π/2=π的电压脉波。脉波的周期为ωTP=π,即uD(ωt)=uD(π+ωt)。在图A-2所取的时间原点情况下,从ωt=0开始的一个周波宽度为ωTP=π(OEGH段)的0≤ωt≤π/2+α期间,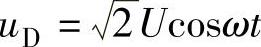 。在OG段(π/2+α)≤ωt≤π期间,uD=
。在OG段(π/2+α)≤ωt≤π期间,uD=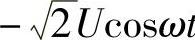 。
。
由式(A-2)、式(A-3)、式(A-4)、式(A-6),即可求得相控整流输出双脉波直流电压uD的直流电压平均值为
图A-2给出了单相桥双脉波整流电路负载电流iD连续时相控角为α整流输出电压uD的波形。从ωt=0开始的第1个脉波的电压uD为OPEFGQMH,在一个交流电源周期T(2π)中,有2个形状相同但相位差2π/2=π的电压脉波。脉波的周期为ωTP=π,即uD(ωt)=uD(π+ωt)。在图A-2所取的时间原点情况下,从ωt=0开始的一个周波宽度为ωTP=π(OEGH段)的0≤ωt≤π/2+α期间,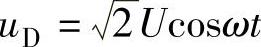 。在OG段(π/2+α)≤ωt≤π期间,uD=
。在OG段(π/2+α)≤ωt≤π期间,uD=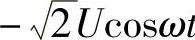 。
。
由式(A-2)、式(A-3)、式(A-4)、式(A-6),即可求得相控整流输出双脉波直流电压uD的直流电压平均值为
uD的n次谐波电压幅值Unm为
uD的n次谐波电压幅值Unm为
不控整流时,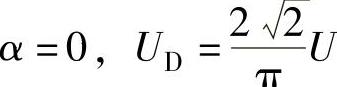 。(A-11)(https://www.xing528.com)
。(A-11)(https://www.xing528.com)
不控整流时,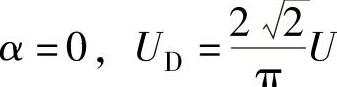 。(A-11)
。(A-11)
3.脉宽为θ的单脉波交流电压u(ωt)
图A-3所示为脉宽为θ的单脉波交流电压u(ωt)。如图A-3a所示,当坐标原点位于N点时,即交流电压u(ωt)为半波对称[u(ωt)=-u(π+ωt)]的奇函数[u(ωt)=-u(-ωt)]时,由式(A-2)、式(A-3)和式(A-4)可得到其傅里叶表达式为
3.脉宽为θ的单脉波交流电压u(ωt)
图A-3所示为脉宽为θ的单脉波交流电压u(ωt)。如图A-3a所示,当坐标原点位于N点时,即交流电压u(ωt)为半波对称[u(ωt)=-u(π+ωt)]的奇函数[u(ωt)=-u(-ωt)]时,由式(A-2)、式(A-3)和式(A-4)可得到其傅里叶表达式为
其中,当θ=π时,
其中,当θ=π时,
当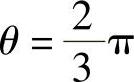 时,
时,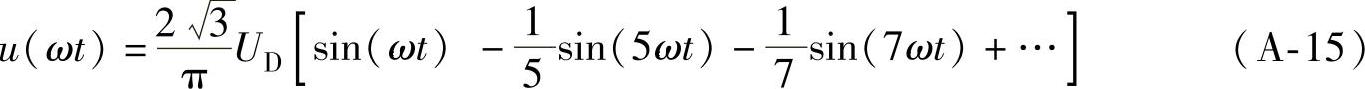
如图A-3b所示,当坐标原点位于M点时,即交流电压u(ωt)为半波对称[u(ωt)=-u(ωt+π)]的偶函数[u(ωt)=u(-ωt)]时,其傅里叶表达式为
当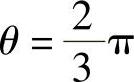 时,
时,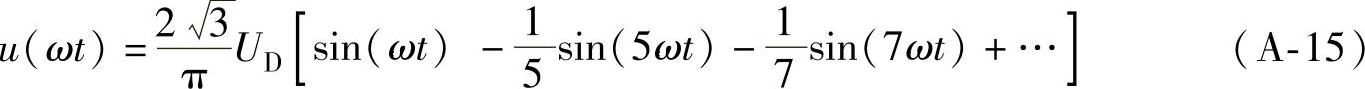
如图A-3b所示,当坐标原点位于M点时,即交流电压u(ωt)为半波对称[u(ωt)=-u(ωt+π)]的偶函数[u(ωt)=u(-ωt)]时,其傅里叶表达式为
其中,当θ=π时,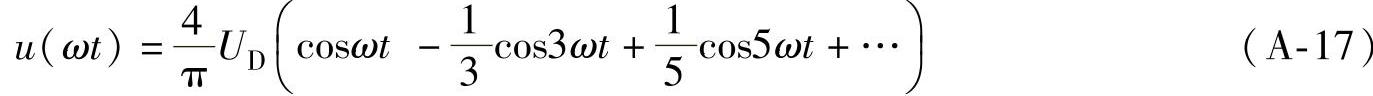
其中,当θ=π时,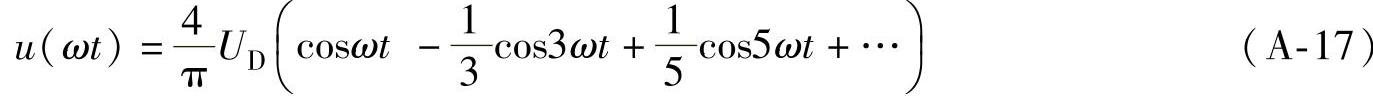
当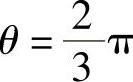 时,
时,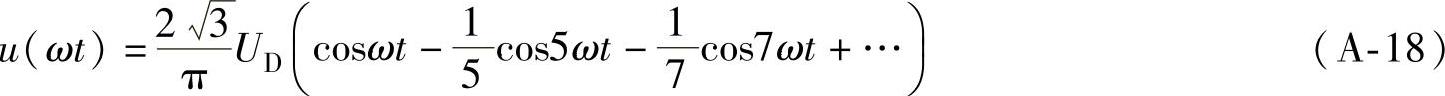 4.脉宽60°、6脉波交流电压
4.脉宽60°、6脉波交流电压
当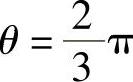 时,
时,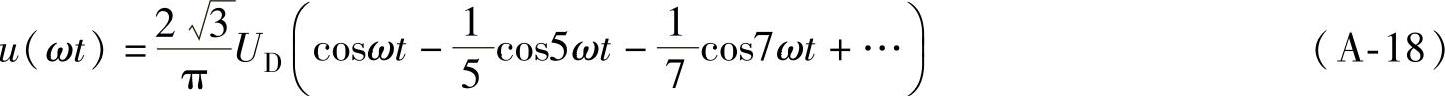 4.脉宽60°、6脉波交流电压
4.脉宽60°、6脉波交流电压
如图A-4所示,当坐标原点位于N点时,幅值为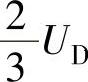 、
、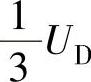 的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
如图A-4所示,当坐标原点位于N点时,幅值为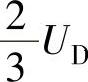 、
、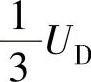 的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
如图A-4b所示,当坐标原点位于M点时,幅值为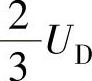 、
、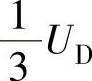 的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
如图A-4b所示,当坐标原点位于M点时,幅值为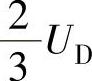 、
、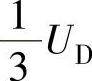 的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
的梯形波半波对称偶函数交流电压u(ωt)的傅里叶表达式为
图A-4 脉宽60°、6脉波交流电压波形
5.脉宽30°、12脉波交流电压
图A-5a所示u(ωt)是一个半波对称的奇函数,其傅里叶表达式为
图A-4 脉宽60°、6脉波交流电压波形
5.脉宽30°、12脉波交流电压
图A-5a所示u(ωt)是一个半波对称的奇函数,其傅里叶表达式为
图A-5b 所示u(ωt)波形与图A-5a相同,但时间坐标相差90°,其傅里叶表达式为
图A-5b 所示u(ωt)波形与图A-5a相同,但时间坐标相差90°,其傅里叶表达式为
图A-5 脉宽30°、12脉波交流电压波形
图A-5 脉宽30°、12脉波交流电压波形
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




