交流电动机变频调速系统优化方案

在过去，调速传动的主流方式是晶闸管直流电动机传动系统。但是直流电动机本身存在一些固有的缺点：①受使用环境条件制约；②需要定期维护；③最高速度和容量受限制等。与直流调速传动系统相对应的是交流调速传动系统，采用交流调速传动系统除了克服直流调速传动系统的缺点外还具有交流电动机结构简单、可靠性高、节能、高精度、快速响应等优点。但交流电动机的控制技术较为复杂，对所需的电力电子变换器要求也较高，所以直到近20年，随着电力电子技术和控制技术的发展，交流调速系统才得到迅速的发展，其应用已在逐步取代传统的直流传动系统。

在交流调速传动的各种方式中，变频调速是应用最多的一种方式。交流电动机的转差功率中转子铜耗部分的消耗是不可避免的，采用变频调速方式时，无论电动机转速高低，转差功率的消耗基本不变，系统效率是各种交流调速方式中最高的，因此采用变频调速具有显著的节能效果，例如采用交流调速技术对风机的风量进行调节，可节约电能30%以上。因此，近年来我国推广应用变频调速技术，已经取得了很好的效果。

1.交-直-交变频器

变频调速系统中的电力电子变流器（简称为变频器），除了在第6章中介绍的交-交变频器外，实际应用最广泛的是交-直-交变频器（Variable Voltage Variable Frequency，VVVF）。交-直-交变频器是由AC-DC、DC-AC两类基本的变流电路组合而成的，先将交流电整流为直流电，再将直流电逆变为交流电，因此这类电路又称为间接交流变流电路。交-直-交变频器与交-交变频器相比，最主要的优点是输出频率不再受输入电源频率的制约。

根据应用场合及负载的要求，变频器有时需要具有处理再生反馈电力的能力。当负载电动机需要频繁、快速制动时，通常要求具有处理再生反馈电力的能力。图7-13所示的是不能处理再生反馈电力的电压型间接交流变流电路。该电路中整流部分采用的是不可控整流，它和电容器之间的直流电压和直流电流极性不变，只能由电源向直流电路输送功率，而不能由直流电路向电源反馈电力。图中逆变电路的能量是可以双向流动的，若负载能量反馈到中间直流电路，将导致电容电压升高，称为泵升电压。由于该能量无法反馈回交流电源，则电容只能承担少量的反馈能量，否则泵升电压过高会危及整个电路的安全。

为使上述电路具备处理再生反馈电力的能力，可采用的几种方法分别如图7-14～图7-16所示。

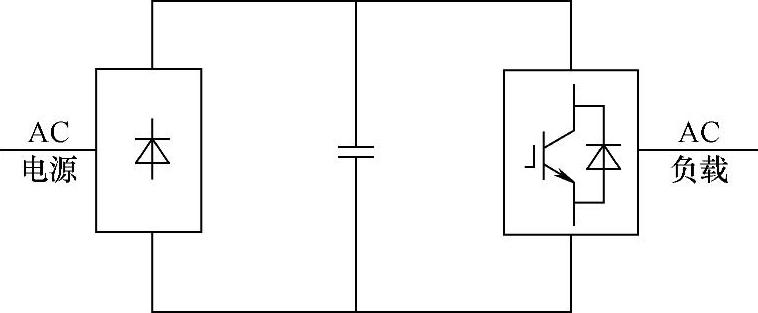
图7-13 不能处理再生反馈电力的电压型间接交流变流电路

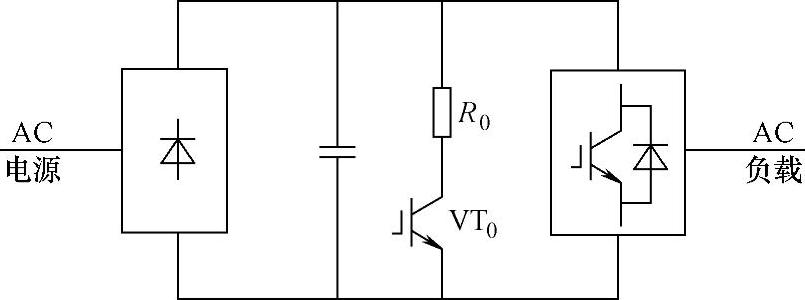
图7-14 带有泵升电压限制电路的电压型间接交流变流电路

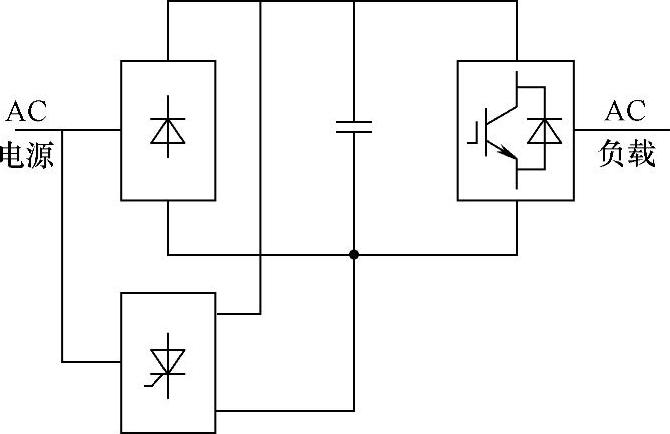
图7-15 利用可控变流器实现再生反馈的电压型间接交流变流电路

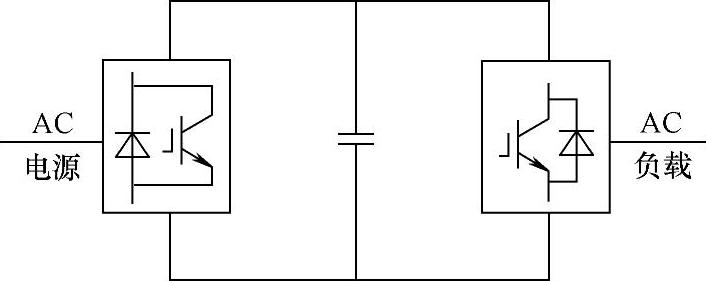
图7-16 整流和逆变均为PWM控制的电压型间接交流变流电路

图7-14电路是在图7-13电路的基础上，在中间直流电容两端并联一个由电力晶体管VT₀和能耗电阻R₀组成的泵升电压限制电路。当泵升电压超过一定数值时，使VT₀导通，把从负载反馈的能量消耗在R₀上。这种电路可应用于对电动机制动时间有一定要求的调速系统中。

当交流电动机负载频繁快速加减速时，上述泵升电压限制电路中消耗的能量较多，能耗电阻R₀也需要较大的功率。这种情况下，希望在制动时把电动机的动能反馈回电网，而不是消耗在电阻上。这时如图7-15所示，需增加一套变流电路，使其工作于有源逆变状态，以实现电动机的再生制动。当负载回馈能量时，中间直流电压上升，使不可控整流电路停止工作，可控变流器工作于有源逆变状态，中间直流电压极性不变，而电流反向，通过可控变流器将电能反馈回电网。

图7-16是整流电路和逆变电路都采用PWM控制的间接交流变流电路，可简称双PWM电路。整流电路和逆变电路的构成可以完全相同，交流电源通过交流电抗器和整流电路连接。通过对整流电路进行PWM控制，可以使输入电流为正弦波并且与电源电压同相位，因而输入功率因数为1，并且中间直流电路的电压可以调节。电动机可以工作在电动运行状态，也可以工作在再生制动状态。此外，改变输出交流电压的相序即可使电动机正转或反转。因此，电动机可实现四象限运行。

该电路输入输出电流均为正弦波，输入功率因数高，且可实现电动机四象限运行，是一种性能较理想的变频电路，但由于整流、逆变部分均为PWM控制且需要采用全控型器件，控制较复杂，成本也较高。

以上讲述的是几种电压型间接交流变流电路的基本原理，下面讲述电流型间接交流变流电路。

图7-17给出了可以再生反馈电力的电流型间接交流变流电路，图中用实线表示的是由电源向负载输送功率时中间直流电压的极性、电流方向、负载电压的极性及功率流向等。当电动机制动时，中间直流电路的电流极性不能改变，要实现再生制动，只需调节可控整流电路的触发延迟角，使中间直流电压反极性即可，如图中虚线所示。与电压型相比，整流部分只用一套可控变流电路，而不像图7-15那样为实现负载能量反馈而采用两套变流电路，系统的整体结构相对简单。

图7-18给出了实现基于上述原理的电路图。为适用于较大容量的场合，将主电路中的器件换为GTO，逆变电路输出端的电容C是为吸收GTO关断时产生的过电压而设置的，它也可以对输出的PWM电流波形起滤波作用。

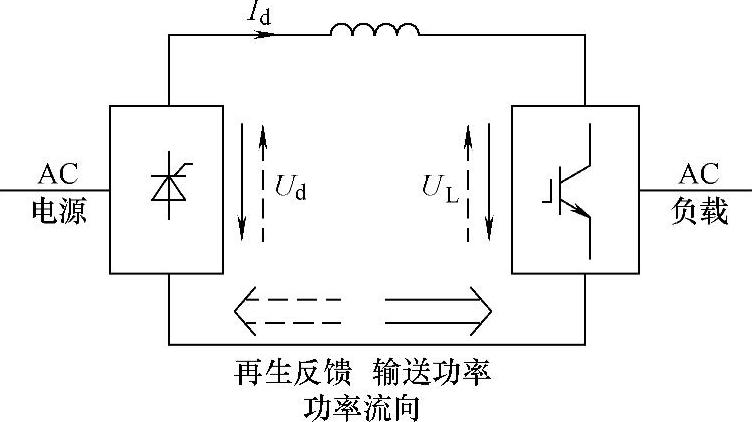
图7-17 采用可控直流的电流型间接交流变流电路

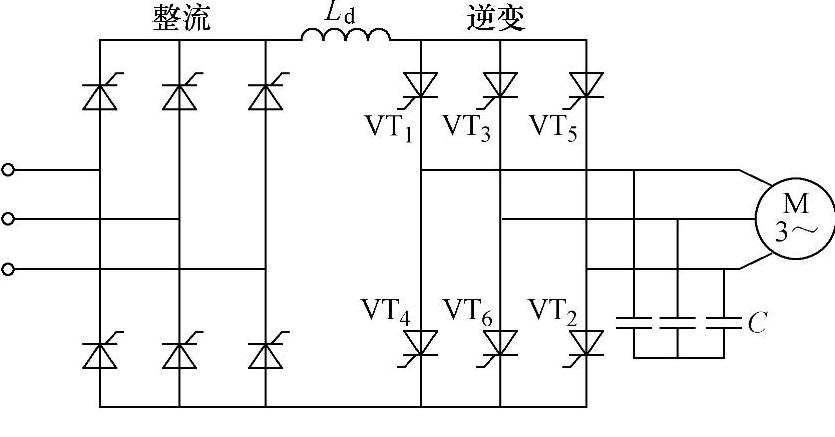
图7-18 电流型交-直-交PWM变频电路

电流型间接交流变流电路也可采用双PWM电路，如图7-19所示。为了吸收换相时的过电压，在交流电源侧和交流负载侧都设置了电容器。和图7-16所示的电压型双PWM电路一样，当向异步电动机供电时，电动机既可工作在电动状态，又可工作在再生制动状态，且可正反转，即可四象限运行。该电路同样可以通过对整流电路的PWM控制使输入电流为正弦波，并使输入功率因数为1。

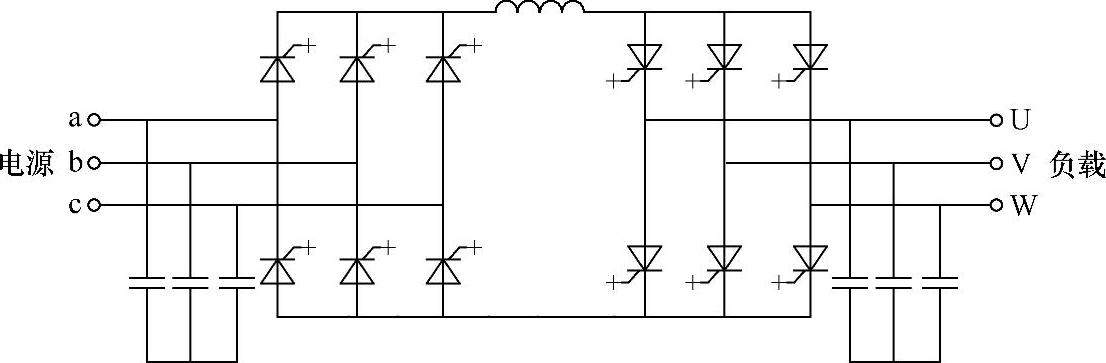
图7-19 整流和逆变均为PWM控制的电流型间接交流变流电路

2.交流电动机变频调速的控制方式

对于笼型异步电动机的定子频率控制方式，有恒压频比（U/f）控制、转差频率控制、矢量控制、直接转矩控制等。这些方式可以获得各具特长的控制性能。以下就分别对几种方式进行简要介绍。

（1）恒压频比控制

异步电动机的转速主要由电源频率和极对数决定。改变电源（定子）频率，就可进行电动机的调速，即使进行宽范围的调速运行，也能获得足够的转矩。为了不使电动机因频率变化导致磁饱和而造成励磁电流增大，引起功率因数和效率的降低，需对变频器的电压和频率之比进行控制，使该比值保持恒定，即恒压频比控制，以维持气隙磁通为额定值。

频比控制是比较简单的控制方式，历史也悠久，目前仍然被大量采用。该方式被用于转速开环的交流调速系统，适用于生产机械对调速系统的静、动态性能要求不高的场合，例如利用通用变频器对风机、泵类进行调速以达到节能的目的。近年来也被大量用于空调等家用电器产品。

图7-20给出了使用PWM控制交-直-交变频器恒压频比控制方式的例子。转速给定既作为调节加减速度的频率f指令值，同时经过适当分压，也被作为定子电压u₁的指令值。该f指令值和u₁指令值之比就决定了（U/f）控制中的压频比。由于频率和电压由同一给定值控制，因此可以保证压频比恒定。

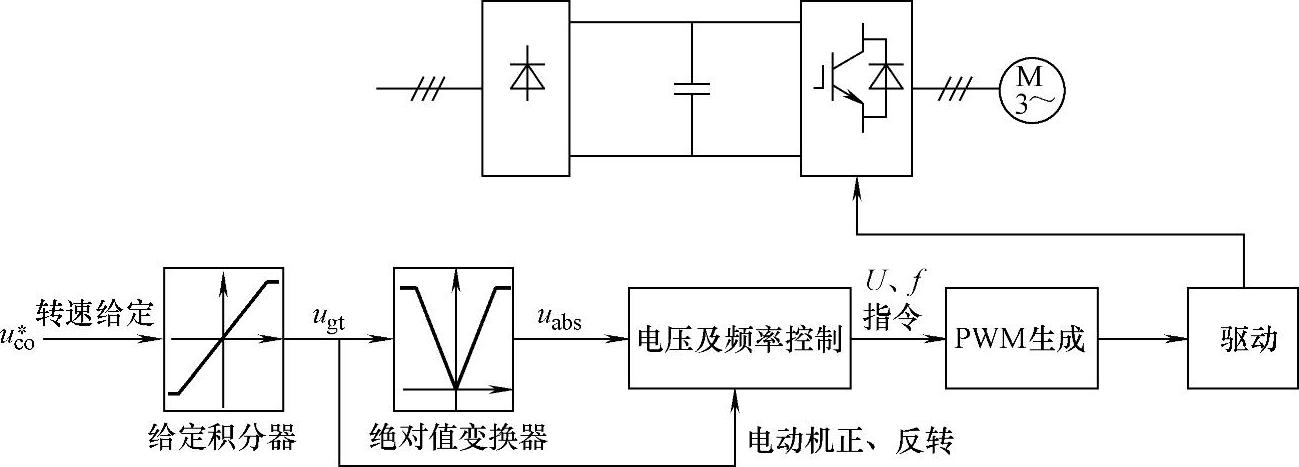
图7-20 采用恒压频比控制的变频调速系统框图

图7-20中，为防止电动机起动电流过大，在给定信号之后加给定积分器，可将阶跃给定信号转换为按设定斜率逐渐变化的斜坡信号u_gt，从而使电动机的电压和转速都平缓地升高或降低。此外，为使电动机实现正反转，给定信号是可正可负的，但电动机的转向由变频器输出电压的相序决定，不需要由频率和电压给定信号反映极性，因此用绝对值变换器将u_gt变换为绝对值的信号u_abs，u_abs经电压频率控制环节处理之后，得出电压及频率的指令信号，经PWM生成环节形成控制逆变器的PWM信号，再经驱动电路控制变频器中IGBT的通断，使变频器输出所需频率、相序和大小的交流电压，从而控制交流电动机的转速和转向。

（2）转差频率控制

前述转速开环的控制方式可满足一般平滑调速的要求，但其静、动态性能均有限，要提高调速系统的动态性能，需采用转速闭环的控制方式。其中一种常用的闭环控制方式就是转差频率控制方式。

从异步电动机的稳态模型可以证明，当稳态气隙磁通恒定时，电磁转矩近似与转差角频率ω_s成正比，如果能保持稳态转子全磁通恒定，则转矩准确地与ω_s成正比。因此，控制ω_s就相当于控制转矩。采用转速闭环的转差频率控制，使定子频率ω₁=ω_r+ω_s，则ω₁随实际转速ω_r增加或减小，得到平滑而稳定的调速，保证了较高的调速范围和动态性能。

但是，这种方法是基于电动机稳态模型的，仍然不能得到理想的动态性能。

（3）矢量控制

异步电动机的数学模型是高阶、非线性、强耦合的多变量系统。前述转差频率控制方式的动态性能不理想，关键在于采用了电动机的稳态数学模型，调节器参数的设计也只是沿用单变量控制系统的概念而没有考虑非线性、多变量的本质。

矢量控制方式基于异步电动机的按转子磁链定向的动态数学模型，将定子电流分解为励磁分量和与此垂直的转矩分量，参照直流调速系统的控制方法，分别独立地对两个电流分量进行控制，类似于直流调速系统中的双闭环控制方式。该方式需要实现转速和磁链的解耦，控制系统较为复杂，但与被认为是控制性能最好的直流电动机电枢电流控制方式相比，矢量控制方式的控制性能具有同等的水平。随着该方式的实用化，异步电动机变频调速系统的应用范围迅速扩大。

（4）直接转矩控制

矢量控制方式的稳态、动态性能都很好，但是控制复杂。为此，又有学者提出了直接转矩控制。直接转矩控制方法同样是基于电动机的动态模型，其控制闭环中的内环，直接采用了转矩反馈，并采用砰-砰控制，可以得到转矩的快速动态响应，并且控制相对要简单许多。

3.多重化、多电平结构变换器

高压电动机的应用极为广泛，它是工矿企业中的主要动力。在冶金、钢铁、石油、化工、水处理等行业的大、中型厂矿中，高压电动机正是主要用于拖动风机、泵类、压缩机及各种大型机械，而且绝大部分都有调速的要求。由于缺少简单可靠、性价比适中的高压调速装置，高压电动机由高压电网供电，采用直接恒速拖动，能耗太大。因此，高性能的高压大功率变频调速装置的市场潜力巨大，应用前景十分广阔。

（1）多重化、单元串联多电平高压变频器的基本结构

单元串联多电平高压变频器采用多个低压的功率单元串联实现高压输出，输入侧采用多重移相降压变压器实现输入电压移相，可有效消除对电网的谐波污染，输出侧采用多电平正弦PWM技术，可适用于任何电压的普通电动机，该方案由美国罗宾康公司在20世纪90年代中期提出，因为每个功率单元结构完全一致，所以将其称为对称单元串联多电平变频器。多重化、多电平高压变频器的典型结构图如图7-21所示。

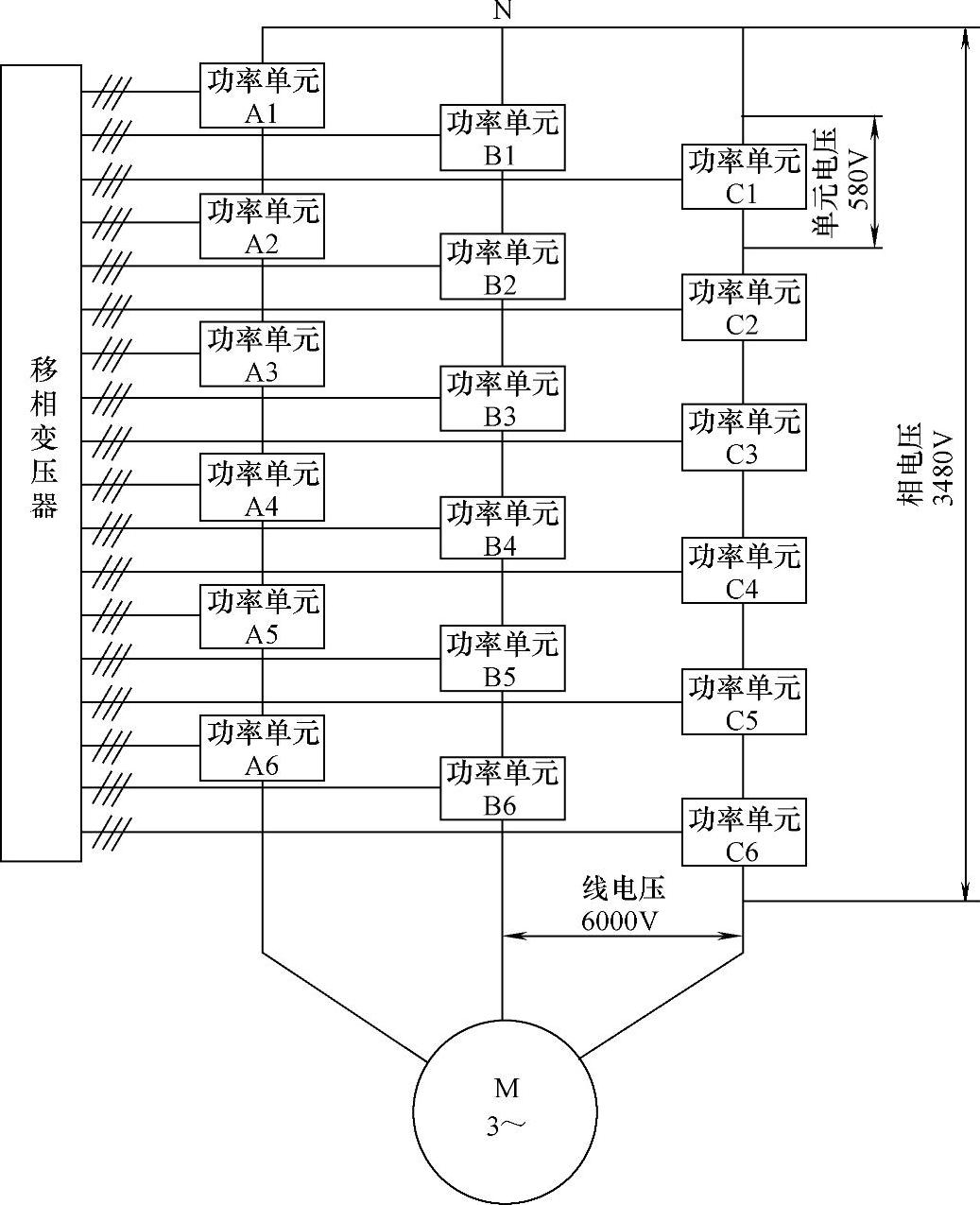
图7-21 多重化、多电平高压变频器的典型结构图

单元串联型多电平高压变频器采用多个独立的低压功率单元串联来实现高压输出，在这种方式中，高电压不是直接输出的，而是通过若干单元的输出串联后叠加得到的。这样对于每个功率单元来说，不必承受高压，可以采用低压的功率器件。此变频器的主电路包含移相整流变压器和功率单元两大部分。

移相整流变压器采用多重化设计，它在设备中主要有三个功能：一是将输入高压变成低压，从而可以用低压的电力电子器件直接逆变而无需串联；二是起到高压和低压间以及低压各绕组间相互绝缘的作用，从而使得各低压单元的输出可以直接串联而无需担心短路和环流问题；三是可以通过将低压各绕组移相，达到移相多重化整流的目的，从而使输入电流谐波急剧减小，变频器对电网基本上没有干扰。

移相整流变压器各二次绕组在绕制时采用延边三角形联结，相互之间有固定的相位差，形成多脉冲整流方式，使得变压器二次侧各绕组（功率单元）的谐波电流互相抵消，不反映到高压侧，从而大大改善了网侧的电流波形，基本消除了变频器对网侧的谐波污染。

功率单元是整台变频器实现变压变频输出的基本单元，变频器的变压变频功能是通过单个功率单元实现的，每个功率单元都相当于一台交-直-交电压型单相输出的低压变频器。功率单元整流侧用二极管三相全桥进行不可控全波整流，中间采用电解电容滤波和储能，该逆变电路为四只IGBT组成的H桥，提供单相等幅的交流PWM波形输出电压。功率单元电路原理图如图7-22所示。

通过控制桥臂上四只IGBT的导通、关断，可以得到三种不同的电平E、0、-E，开关状态见表7-1。

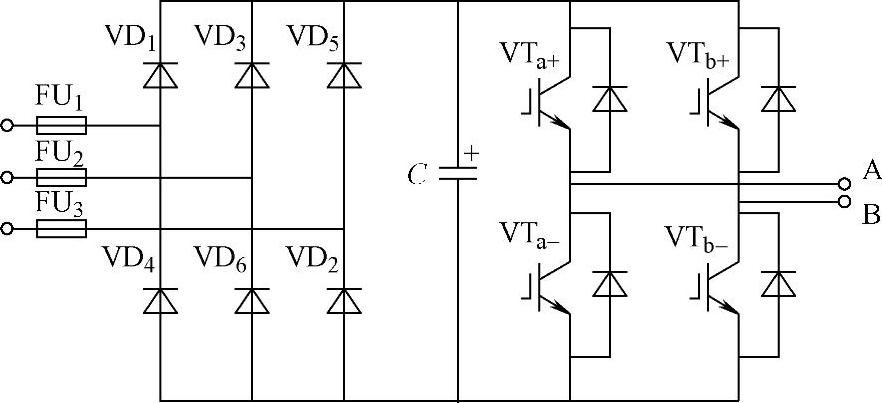
图7-22 功率单元电路原理图

表7-1 H桥逆变器三电平状态表(www.xing528.com)

6kV单元串联的高压变频器的总体输出侧的电压叠加示意图如图7-23所示。总高电压输出由每个功率单元的U、V相输出串联而得到。对于n级串联的系统，相电压有2n+1个电平，线电压有4n+1个电平，du/dt很小，每个功率单元提供1/n的输出电压，1/（3n）的输出功率。

每一相输出的相电压，是N个功率单元输出电压的串联叠加，即

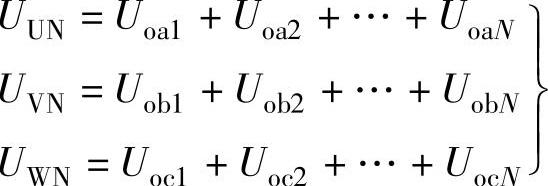
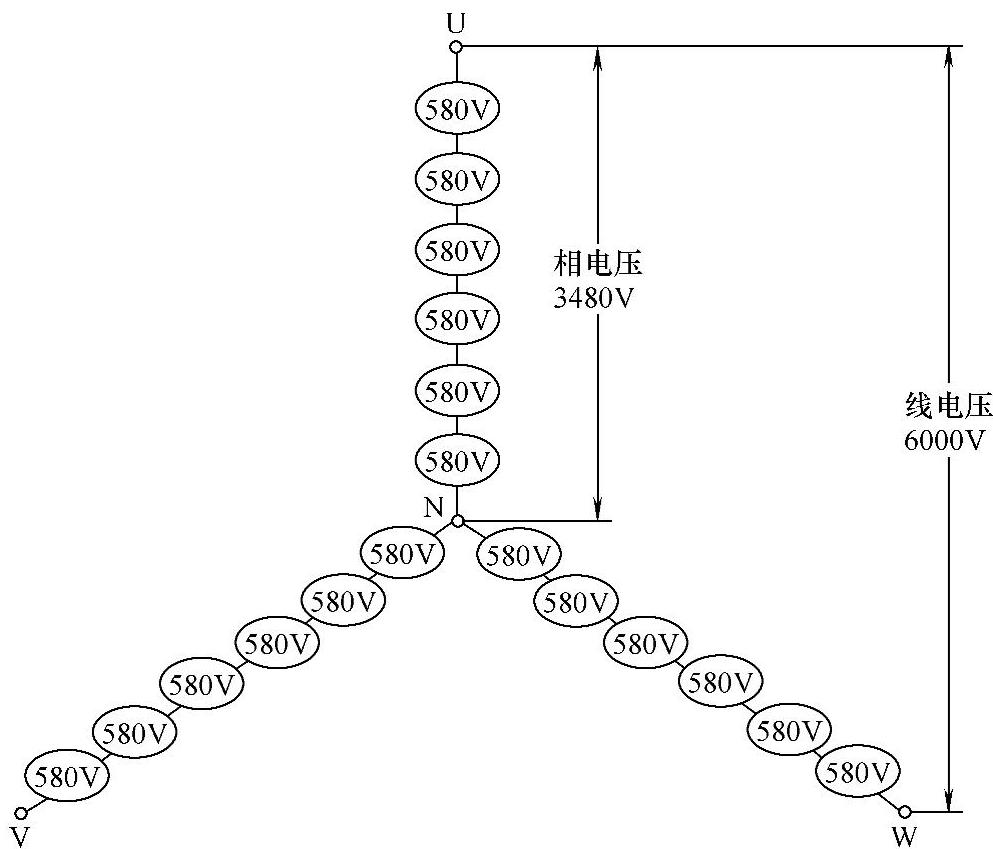
图7-23 6kV电压叠加示意图

单元串联多电平高压变频器具有以下特点：

①电流谐波小，对电网没有谐波污染，无需谐波抑制装置。

②输入功率因数高，网侧不需要调节功率因数补偿装置。

③输出阶梯正弦PWM波形，可直接适用于任何电压的普通电动机。不需任何的滤波装置。

④在某个功率单元出现故障时，可降额运行，不停机。

⑤输出电压可达到3kV、6kV、10kV等高电压等级。

（2）12阶梯波、24阶梯波高电压大容量变频器主电路

当系统容量较大时，输入谐波问题是大容量变频器的一个突出问题。对交-直-交变频调速系统而言，常用的整流器均采用晶闸管相控整流电路或二极管整流电路，直流侧采用电容滤波，这使交流侧的电流呈尖峰性而非正弦波。大量使用由这些电路构成的装置已成为电力系统中的主要谐波源，且消耗大量的无功功率。变频器输出的谐波电流也会使电动机损耗增加，因而发热增加，电动机出力下降。在变频器输入侧消除谐波的方法很多，其中之一就是利用整流器输入电路产生谐波的相位差把谐波分量相互抵消，多脉波就是利用并联的两组以上脉波电路谐波相位差，相互抵消而成的。构成的方法有两种：①由交流电路直接并接两组整流电路；②输入侧连接隔离变压器，由隔离变压器二次绕组输送给各整流单元，形成各种脉波电路。

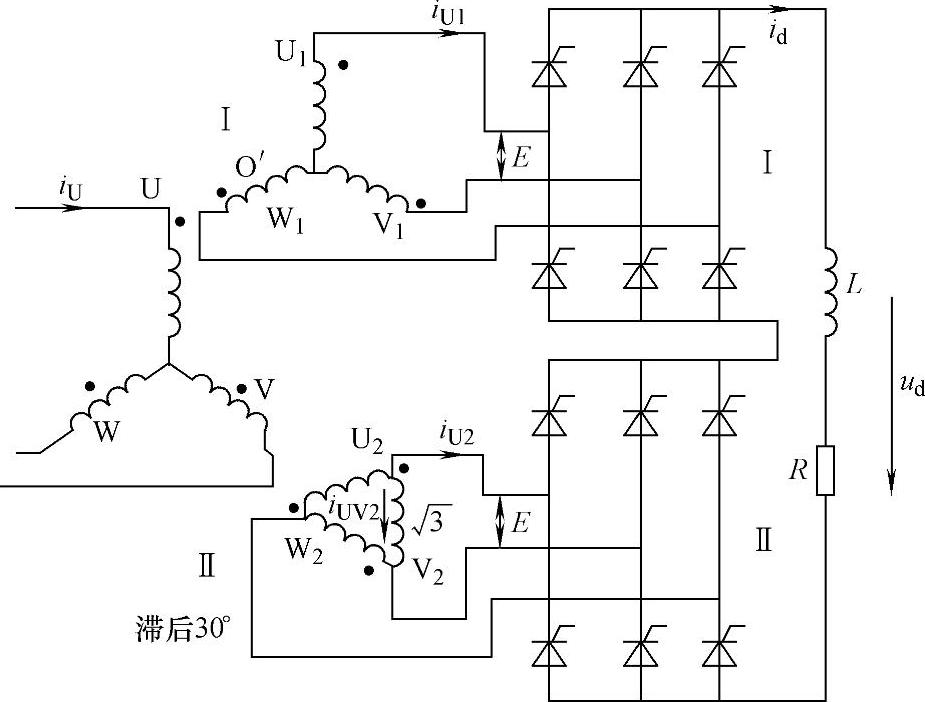
图7-24 脉波整流电路结构

在下面分析中不考虑变压器漏抗引起的重叠角，并且假设整流变压器各绕组的线电压之比为1∶1。为了分析方便，假定直流环节电流为恒定值，这种条件一般在电流源型变频器中近似成立，在电压源型变频器中，直流环节电流则为脉动状。

1）移相30°构成的12脉波整流电路。

图7-24是这种电路的原理图，整流变压器二次绕组分别采用星形和三角形联结，构成相位差30°、大小相等的两组电压，加到两组整流桥上。因绕组连接方式不同，变压器一次绕组和两组二次绕组的匝数比为1∶1∶3。

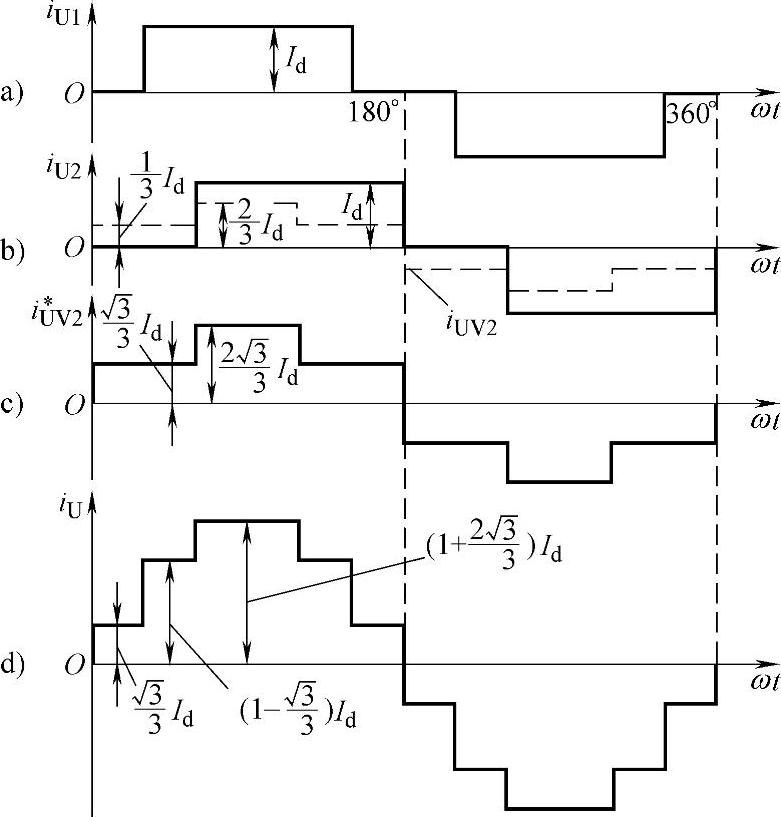
图7-25 脉波整流电路电流波形

图7-25为该电路输入电流波形图。其中，图7-25c的i_UV2是第Ⅱ组整流桥i_UV2折算到变压器一次侧U相绕组中的电流。图7-25d中输入电流I_U为图7-25a的i_U1和图7-25c的i_UV2之和。对图7-25波形进行傅里叶分析，可得其基波幅值A₁和n次谐波幅值A_n，分别为

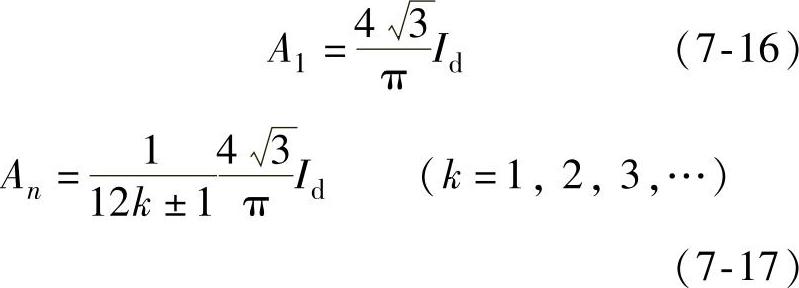
即输入电流谐波次数为11、13、23、25、37、…，其幅值与次数成反比。

该电路的其他特征如下：

①输入电流有效值I₁=1.577I_d。

②输入电流总畸变率THD_i=0.1522。

③位移相数cosφ=cosα。

④基波因数。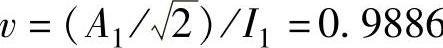

⑤功率因数λ=vcosφ₁=0.9886cosα。

2）移相20°构成的18脉波整流电路。

图7-26是其电路图，其中整流桥采用简化画法。对于整流变压器来说，采用星形、三角形联结组合无法移相20°，这里第Ⅰ、Ⅲ绕组采用了延边三角形曲折联结。这种连接方式的每相由对应于一次侧不同绕组的匝数比可以实现任意角度的相移。以一次侧每相绕组为N，通过求解图7-26中第Ⅰ组桥U₁相绕组的三角形可得图中绕组N_x、N_y的匝数分别为

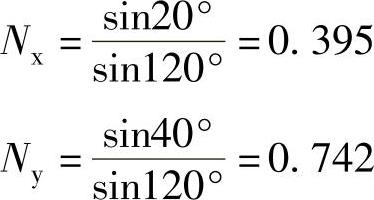
图7-27 为整流变压器一次侧输入电流i_U波形，其基波和谐波幅值分别为

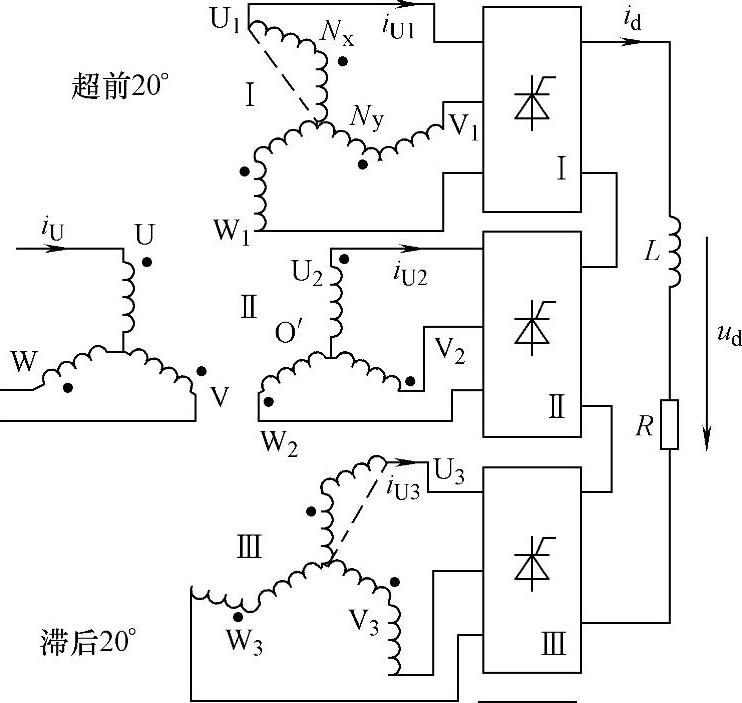
图7-26 脉波整流电路结构

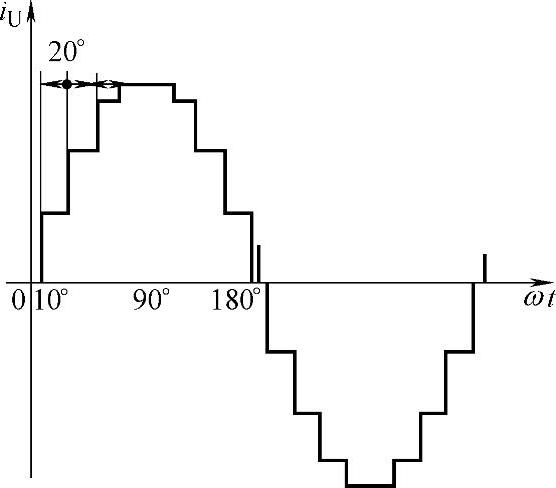
图7-27 脉波整流电路输入电流波形

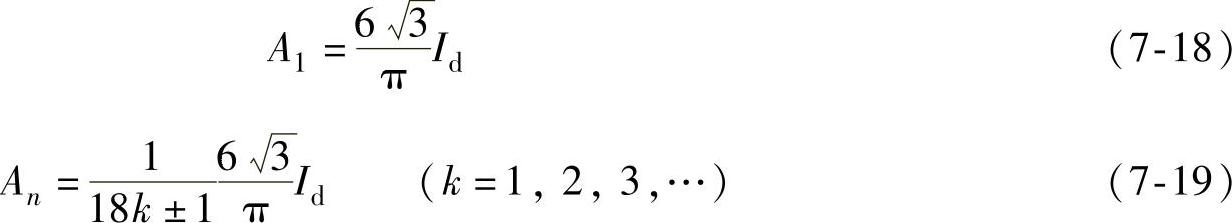
即输出电流谐波次数为17、19、35、37、53、55、…，其幅值与次数成反比而降低。

该电路的其他特性如下：

①输入电流有效值I₁=2.351I_d。

②输入电流总畸变率THD_i=0.1011。

③位移相数cosφ=cosα。

④基波因数。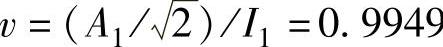

⑤功率因数λ=vcosφ₁=0.9949cosα。

所以，通过两个相位差30°的变压器绕组分别供电给两个三相整流电路可构成12脉波整流电路，其网侧电流仅含12k±1次谐波。类似地，通过依次相差15°的四个变压器绕组分别供电给四个三相整流桥就可获得24脉波整流电路，其网侧电流桥就可获得30脉波整流电路，其网侧电流仅含30k±1次谐波。

作为一般规律，以m个相位依次相差π/（3m）的变压器绕组分别供电给m个三相整流桥便可获得6m脉波整流电路，其网侧电流仅含6mk±1次谐波，而且各次谐波电流的有效值与其谐波次数成反比，而与基波电流有效值的比值是谐波次数的倒数。另外，其位移功率因数均为cosα，不随整流脉波数的增加而提高，但基波因数随着整流脉波数的提高而提高，所以总体输入功率因数也跟着提高。对于二极管不可控整流电路而言，相电流相对于相电压的触发延迟角α一般小于15°，对应的位移功率因数大于0.966，所以采用多重化（18脉波以上）的二极管整流电路，总的输入功率因数基本上可保持在0.95以上。

3）多脉波变频器实例。

西门子的SIMOVERT MV装置如图7-28所示，为了实现对电网冲击低、谐波小，这种装置有三种不同的整流方式来适应各种不同要求的供电配置。

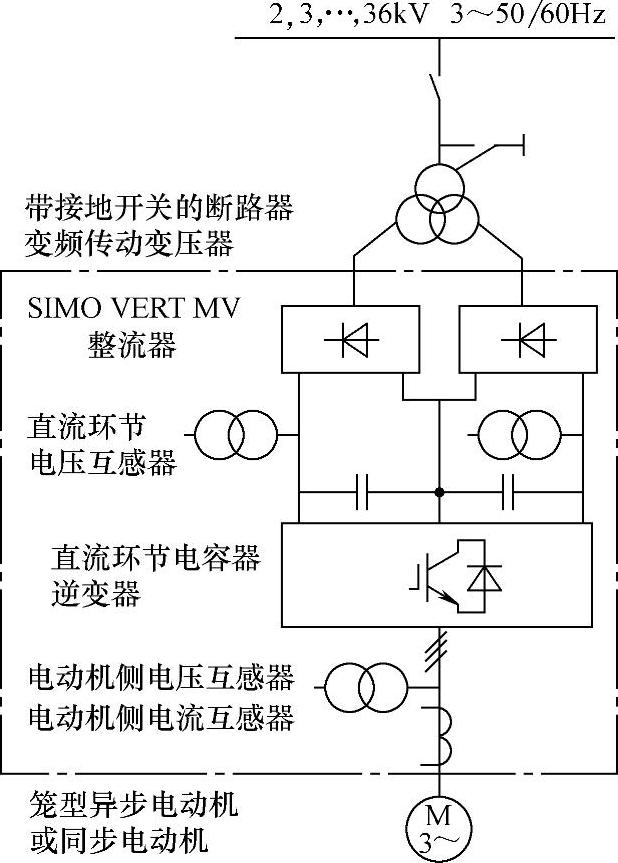
图7-28 西门子的SIMOVERT MV装置

第一种标准配置，采用12脉波二极管整流器，如图7-29所示，这是成本最低的方案，cosφ＞0.96，谐波电流低。

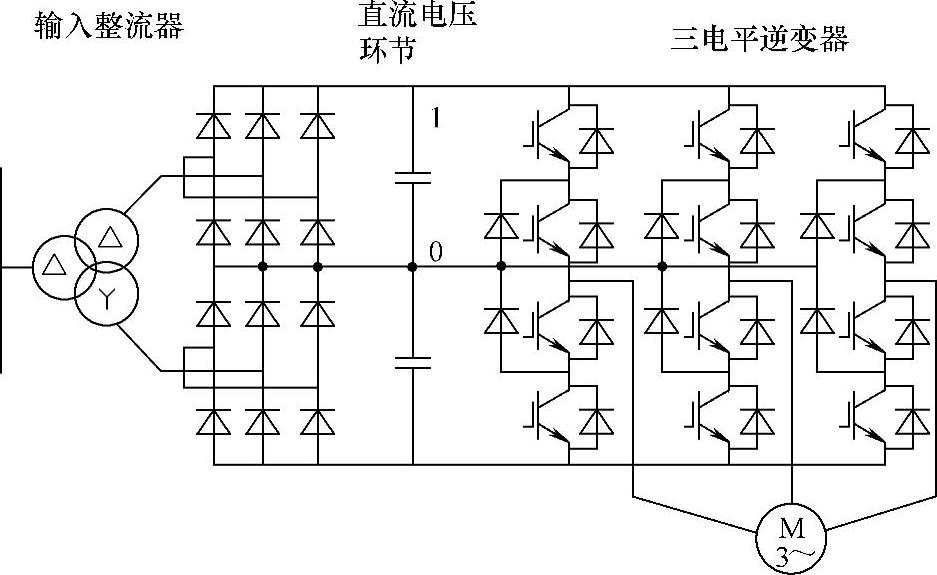
图7-29 12脉波二极管整流的SIMOVERT MV装置

第二种采用可选的24脉冲二极管整流器，输出变压器应有四个二次侧，24只二极管。它适用于要求反馈电网谐波特别少、干扰特别低的场合，但是价格会昂贵些。

第三种采用有源前端的AFE高性能三电平PWM有源变流器。它可提供四象限运行，不仅可实现cosφ=1.0，而且可对同一线路上其他负载进行无功补偿。若具有输入滤波器的AFE有源前端整流器，几乎可以不向电网反馈谐波电流。当然，这种采用AFE高动态性能的SIMOVERT MV装置，控制电路复杂，价格昂贵，一般情况不采用。

SIMOVERT MV装置三相逆变器采用三电平PWM技术，可获得优良的输出电压特性，以及谐波分量小的正弦电流波形，使电动机有极佳的转矩特性，降低电动机损耗。电力电子器件采用全新的HV-IGBT技术，使装置的结构简单紧凑，不需要缓冲电路，可靠性大大提高。