晶闸管直流电动机调速系统优化方案

晶闸管可控整流装置带直流电动机负载组成的系统，习惯称为晶闸管直流电动机系统，是电力拖动系统中主要的一种，也是可控整流装置的主要用途之一。

1.工作于整流状态时

直流电动机负载除本身有电阻、电感外，还有一个反电动势E。如果暂不考虑电动机的电枢电感，则只有当晶闸管导通相的变压器二次电压瞬时值大于反电动势时才有电流输出。为了平稳负载电流的脉动，通常在电枢回路串联一平波电抗器，保证整流电流在较大范围内连续，图7-7为三相半波带电动机负载且加平波电抗器时的电压、电流波形。

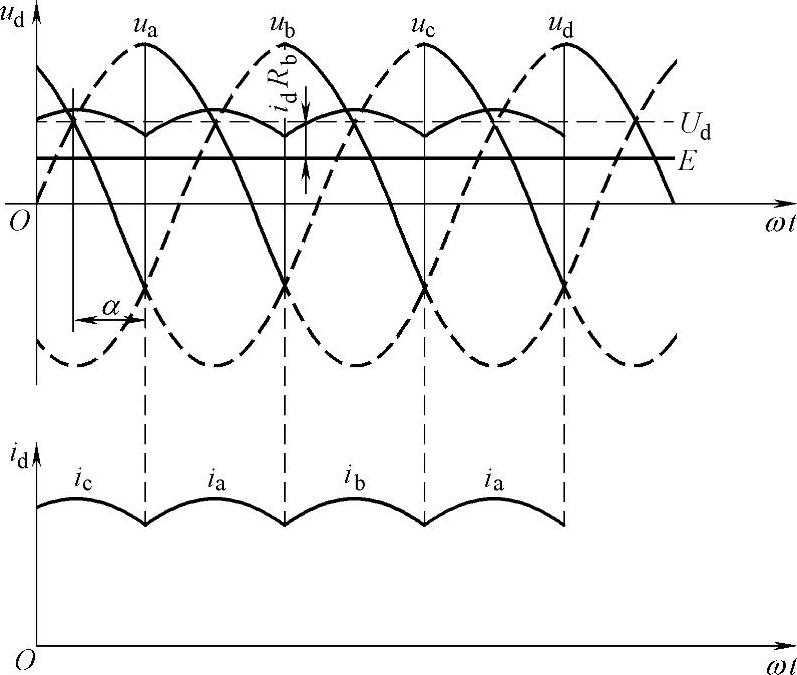
图7-7三相半波带电动机负载且加平波电抗器时的电压、电流波形

触发晶闸管，待电动机起动达到稳态后，虽然整流电压的波形脉动较大，但由于电动机有较大的机械惯量，故其转速和反电动势都基本无脉动。此时整流电压的平均值由电动机的反电动势及电路中负载平均电流I_d所引起的各种电压降所平衡。整流电压的交流分量则全部降落在电抗器上。由I_d引起的电压降有下列四部分：变压器的电阻压降I_dR_b，其中R_b为变压器的等效电阻，它包括变压器二次绕组本身的电阻以及一次绕组电阻折算到二次侧的等效电阻；晶闸管本身的管压降ΔU，它基本上是一恒值；电枢电阻压降I_dR_M；由重叠角引起的电压降3X_BI_d/（2π）。此时，整流电路直流电压的平衡方程为

U_d=E_M+R_∑I_d+ΔU （7-1）

式中，。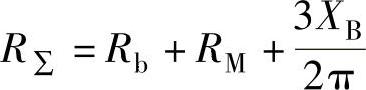

在电动机负载电路中，电流I_d由负载转矩所决定。当电动机的负载较轻时，对应的负载电流也小。在小电流情况下，特别是在低速时，由于电感的储能减小，往往不足以维持电流连续，从而出现电流断续现象。这时整流电路输出的电压和电流波形与电流连续时有差别，因此晶闸管电动机系统有两种工作状态：一种是工作在电流较大时的电流连续工作状态，另一种是工作在电流较小时的电流断续工作状态。

（1）电流连续时电动机的机械特性

从电力拖动的角度来看，电动机的机械特性是表示其性能的一个重要方面，由生产工艺要求的转速、静差度即由机械特性决定。

在电动机学中，已知直流电动机的反电动势为

E_M=C_eϕn （7-2）

式中，C_e为由电动机结构决定的电动势常数；ϕ为电动机磁场每对磁极下的磁通量，单位为Wb；n为电动机的转速，单位为r/min。

可根据整流电路电压平衡方程式（7-1），得到不同触发延迟角α时E_M与I_d的关系。因为U_d=1.17U₂cosα，因此反电动势特性方程为

E_M=1.17U₂cosα-R_ΣI_d-ΔU （7-3）

转速与电流的机械特性关系式为

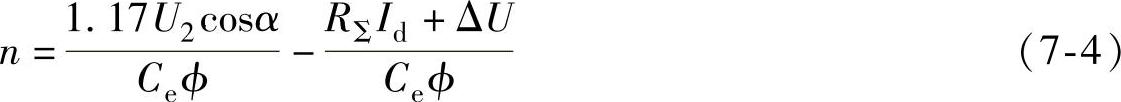
根据式（7-4）得出不同α时n与I_d的关系，如图7-8所示。图中ΔU的值一般为1V左右，所以忽略。可见其机械特性与由直流发电机供电时的机械特性是相似的，是一组平行的直线，其斜率由于内阻不一定相同而稍有差异。调节α，即可调节电动机的转速。

同理，可列出三相桥式全控整流电路电动机负载时的机械特性方程为

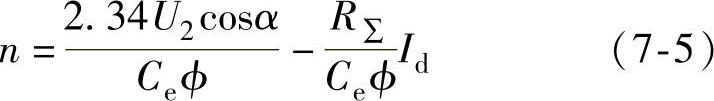
（2）电流断续时电动机的机械特性

由于整流电压是一个脉动的直流电压，当电动机的负载减小时，平波电抗器中的电感储能减小，致使电流不再连续，此时电动机的机械特性也呈现出非线性。

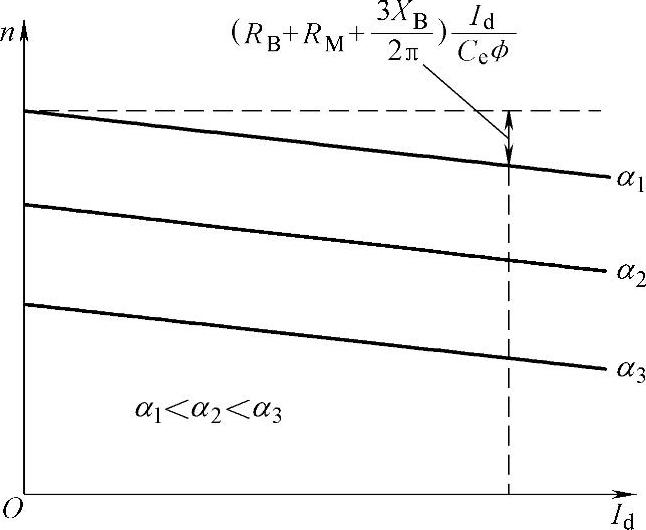
图7-8三相半波电流连续时以电流表示的电动机机械特性

根据电流连续时反电动势的公式（7-3），例如α=60°时，若I_d=0，忽略ΔU，此时的反电动势E₀′=1.17U₂cos60°=0.585U₂，这是电流连续时的理想空载反电动势，如图7-9中反电动势特性的虚线与纵轴的相交点。实际上，当I_d减小至某一定值I_dmin以后，电流变为断续，这个E₀′是不存在的，真正的理想空载点E₀远大于此值，因为α=60°时晶闸管触发导通时的相电压瞬时值为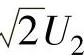，它大于E′₀，因此必然产生电流，这说明并不是空载点。只有当反电动势E等于触发导通后相电压的最大值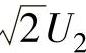时，电流才等于零，因此图7-9中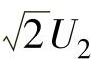才是实际的理想空载点。同样可分析得出，在电流断续情况下，只要α≤60°，电动机的实际空载反电动势都是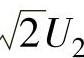。当α＞60°以后，空载反电动势将由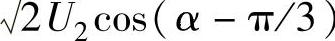决定。可见，当电流断续时，电动机的理想空载转速抬高，这是电流断续时电动机机械特性的第一个特点。观察图7-9可得知此时机械特性的第二个特点是，在电流断续区内电动机的机械特性变软，即负载电流变化很小也可引起很大的转速变化。

根据上述分析，可得不同α时的反电动势特性曲线如图7-10所示。α大的反电动势特性，其电流断续区的范围（以虚线表示）要比α小时的电流断续区大，这是由于α越大，变压器加到晶闸管阳极上的负电压时间越长，电流要维持导通，必须要求平波电抗器储存较大的磁能，而电抗器L为一定值的情况下，要有较大的电流I_d才行。故随着α的增加，进入断续区的电流值加大。这是电流断续时电动机机械特性的第三个特点。

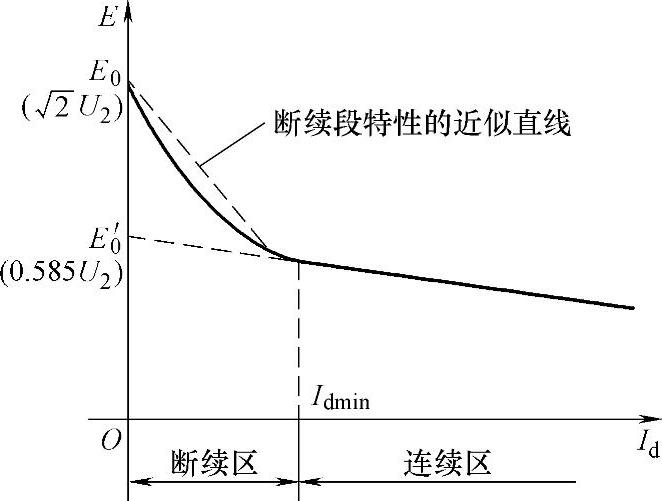
图7-9 电流断续时电动势的特性曲线

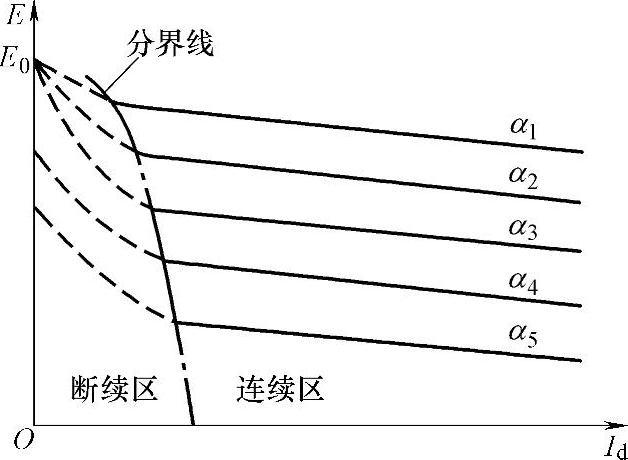
图7-10 考虑电流断续不同α时的反电动势特性曲线α₁＜α₂＜α₃＜60°，α₅＞α₄＞60°

电流断续时电动机机械特性可由下面三个式子准确地得出，限于篇幅，推导过程从略。

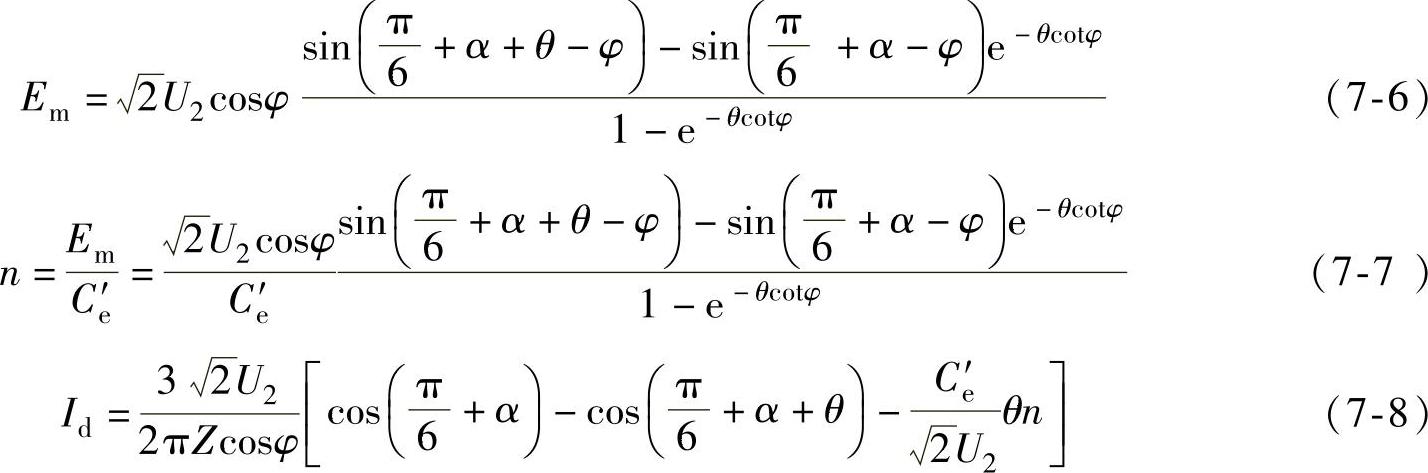
式中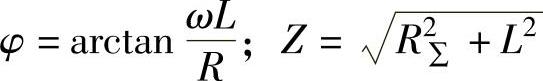，；L为回路总电感。式（7-6）～式（7-8）均为超越方程，需采用迭代的方法求解，在导通角θ从0～2π/3的范围内，根据给出的θ值以及R_∑、L值，求出相应的n和I_d，从而做出断续区的机械特性曲线，如图7-9所示。对于不同的R_∑、L和α值，特性也将不同。

一般只要主电路电感足够大，就可以只考虑电流连续段，完全按线性处理。当低速轻载时，断续作用显著，可改用另一段较陡的特性来近似处理（见图7-9），其等效电阻比实际的电阻R要大一个数量级。(www.xing528.com)

整流电路为三相半波时，在最小负载电流为I_dmin时，为保证电流连续所需的主电路电感量L（单位：mH）为

对于三相桥式全控整流电路带电动机负载的系统，有

其中，L包括整流变压器的漏电感、电枢电感和平波电抗器的电感，前者数值都较小，有时可忽略；I_dmin一般取电动机额定电流的5%～10%。

因为三相桥式全控整流电压的脉动频率比三相半波的高一倍，因而所需平波电抗器的电感量也可相应减小约一半，这也是三相桥式整流电路的一大优点。

2.工作于有源逆变状态时

对工作于有源逆变状态时电动机机械特性的分析，和整流状态时类同，可按电流连续和断续两种情况来进行。

（1）电流连续时电动机的机械特性

主电路电流连续时的机械特性由电压平衡方程式U_d-E_M=I_dR_∑决定。

逆变时由于U_d=-U_d0cosβ，E_M反接，得

E_M=-（U_d0cosβ+I_dR_∑） （7-11）

因为E_M=C_e′n，可求得电动机的机械特性方程式为

式中，负号表示逆变时电动机的转向与整流时相反。对应不同的逆变角时，可得到一组彼此平行的机械特性曲线族，如图7-11中第4象限虚线以右所示。可见调节β就可改变电动机的运行转速，β值越小，相应的转速越高；反之则转速越低。图7-11中还画出了当负载电流I_d降低到临界连续电流以下时的特性，如图7-11中的虚线以左所示，即逆变状态下电流断续时的机械特性。

（2）电流断续时电动机的机械特性

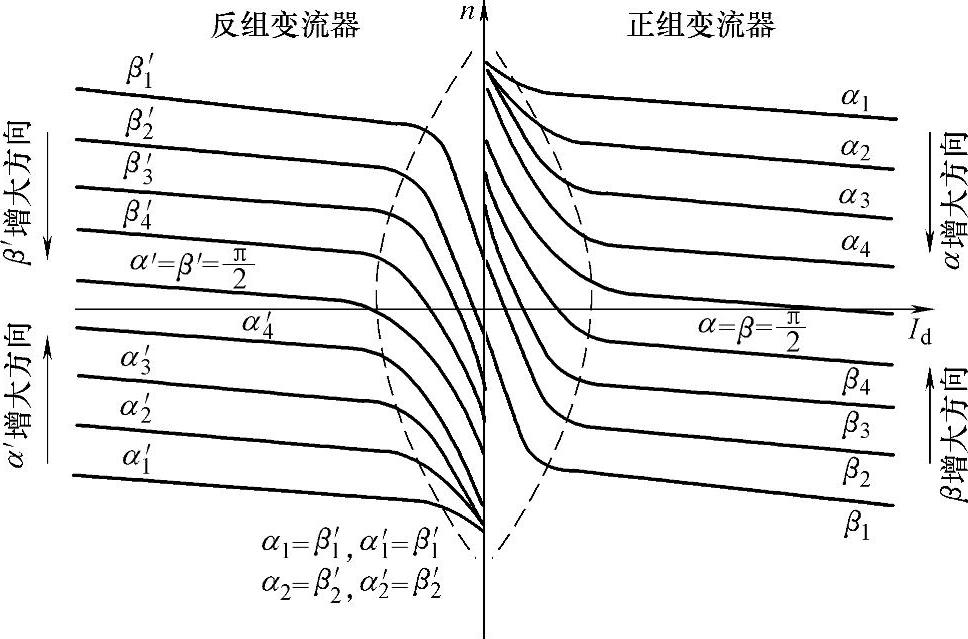
图7-11 电动机在四象限中的机械特性曲线

电流断续时电动机的机械特性方程可沿用整流时电流断续的机械特性表达式，只要把α=π-β代入式（7-6）、式（7-7）和式（7-8），便可得E_M、n与I_d的表达式，求出三相半波电路工作于逆变状态且电流断续时的机械特性，即

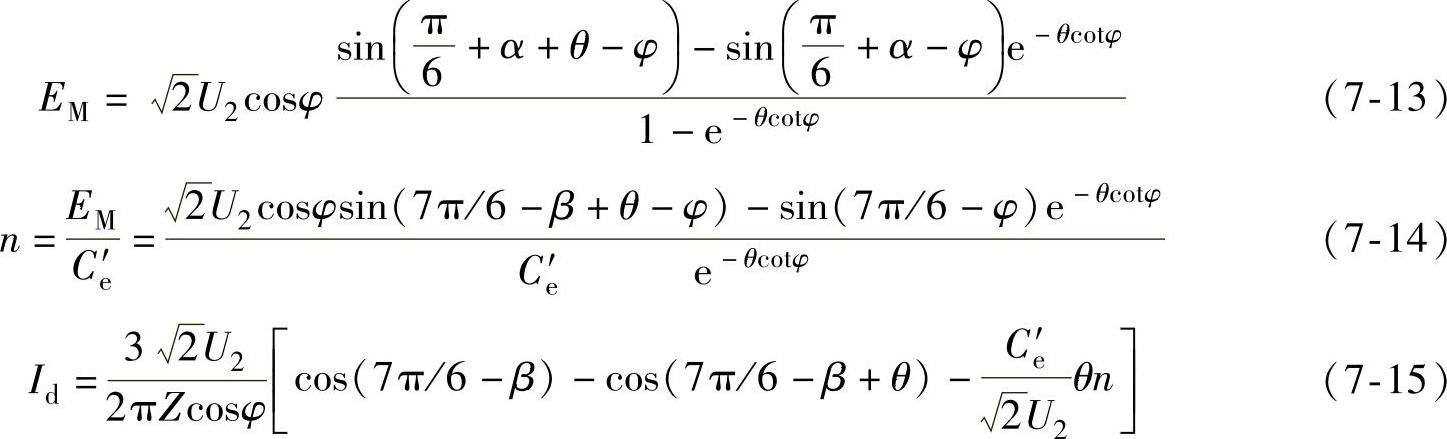
分析结果表明，当电流断续时，电动机的机械特性不仅和逆变角有关，而且和电路参数、导通角等有关系。根据上述公式，取定某一β值，根据不同的导通角θ，如π/6、π/3和π/2，就可求得对应的转速和电流，绘出逆变电流断续时电动机的机械特性，即由图7-11中第4象限虚线以左的部分可以看出，它与整流时十分相似：理想空载转速上翘很多，机械特性变软，且呈现非线性，这充分说明逆变状态的机械特性是整流状态的延续，纵观触发延迟角α由小变大（如π/6～5π/6），电动机的机械特性则逐渐由第1象限往下移，进而到达第4象限。逆变状态的机械特性同样还可表示在第2象限内，与它对应的整流状态的机械特性则表示在第3象限里，如图7-11所示。

应该指出，图7-11中第1、第4象限的特性和第3、第2象限中的特性是分别属于两组变流器的，它们输出整流电压的极性彼此相反，故分别标以正组和反组变流器。电动机的运行工作点由第1（第3）象限的特性，转到第2（第4）象限的特性时，表明电动机由电动运行转入发电制动运行。相应变流器的工况由整流转为逆变，使电动机轴上储存的机械能逆变为交流电能送回电网。电动机在各象限中的机械特性，对分析直流可逆拖动系统是十分有用的。

3.直流可逆电力拖动系统

图7-12为两套变流装置反并联连接的可逆电路。图7-12a是以三相半波有环流接线为例，图7-12b是以三相全控桥的无环流接线为例阐明其工作原理的。与双反星形电路相似，环流是指只在两组变流器之间流动而不经过负载的电流。电动机正向运行时都是由一组变流器供电的；反向运行时，则由两组变流器供电。根据对环流的不同处理方法，反并联可逆电路又可分为几种不同的控制方案，如配合控制有环流（α=β工作制）、可控环流、逻辑控制无环流和错位控制无环流等。不论采用哪一种反并联供电电路，都可使电动机在四个象限内运行。如果在任何时间内，两组变流器中只有一组投入工作，则可根据电动机所需的运转状态来决定哪一组变流器工作及其相应的工作状态：整流或逆变。图7-12c绘出了对应电动机四象限运行时两组变流器（简称正组桥、反组桥）的工作情况。

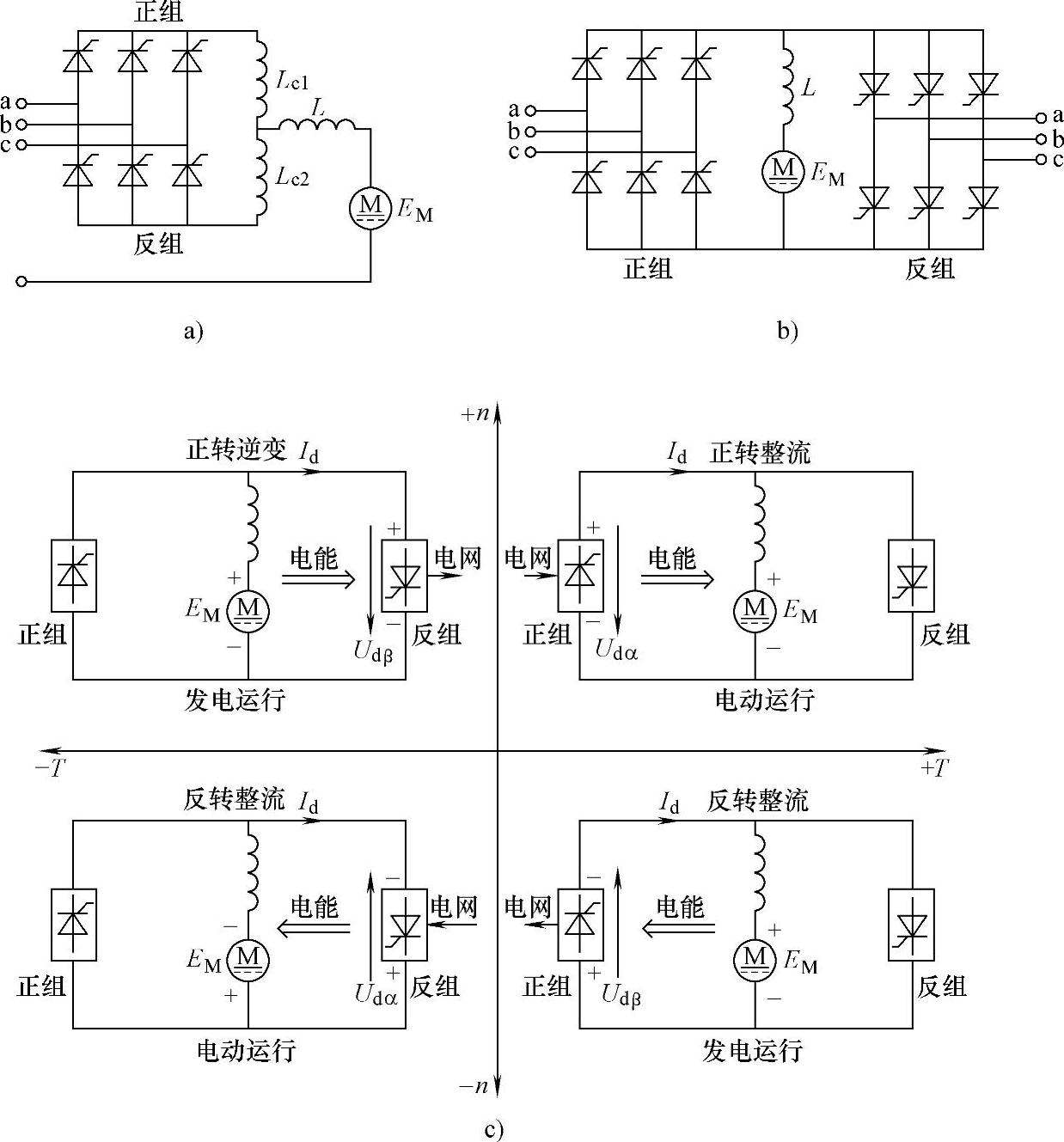
图7-12 两组变流器的反并联可逆线路

a）三相半波有环流 b）三相全控桥无环流 c）变流器四象限运行的工作情况

第1象限：正转，电动机作电动运行，正组桥工作在整流状态，α₁＜π/2，E_M＜U_dα（下标中有α表示整流）。

第2象限：正转，电动机作发电运行，反组桥工作在逆变状态，β₂＜π/2（α₂＞π/2），E_M＞U_dβ（下标中有β表示逆变）。

第3象限：反转，电动机作电动运行，反组桥工作在整流状态，α₂＜π/2，E_M＜U_dα。

第4象限：反转，电动机作发电运行，正组桥工作在逆变状态，β₁＜π/2（α₂＞π/2），E_M＞U_dβ。

直流可逆拖动系统，除了能方便地实现正反向运转外，还能实现回馈制动，把电动机轴上的机械能（包括惯性能、位势能）变为电能输送到电网中去，此时电动机的电磁转矩变成制动转矩。图7-12c所示电动机在第1象限正转，电动机从正组桥取得电能。如果需要反转，先应使电动机迅速制动，就必须改变电枢电流的方向，但对正组桥来说，电流不能反向，需要切换到反组桥工作，并要求反组桥在逆变状态下工作，保证U_dβ与E_M同极性相接，使得电动机的制动电流I_d=（E_M-U_dβ）/R_∑限制在容许范围内。此时电动机进入第2象限作正转发电运行，电磁转矩变成制动转矩，电动机轴上的机械能经反组桥逆变为交流电能回馈到电网。改变反组桥的逆变角β，就可改变电动机的制动转矩。为了保持电动机在制动过程中有足够的转矩，一般应随着电动机转速的下降，不断地调节β，使之由小变大直至β=π/2（n=0），如继续增大β，即α＜π/2，反组桥将转入整流状态下工作，电动机开始反转进入第3象限的电动运行。以上就是电动机正转到反转的全过程。同样，电动机从反转到正转，其过程则由第3象限经第4象限最终运行在第1象限上。

对于α=β配合控制的有环流可逆系统，当系统工作时，对正、反两组变流器同时输入触发脉冲，并严格保证α=β的配合控制关系，假设正组桥为整流，反组桥为逆变，即有α₁=β₁，U_dα1=U_dβ2，且极性相抵消，两组变流器之间没有直流环流。但两组变流器的输出电压瞬时值不等，会产生脉动环流。为防止环流只流经晶闸管而使电源短路，必须串入环流电抗器L_c限制环流。

工程上使用较广泛的逻辑无环流可逆系统不设置环流电抗器，如图7-12b所示。这种无环流可逆系统采用的控制原则是：两组桥在任何时刻只有一组投入工作（另一组关断），所以在两组桥之间就不存在环流；但当两组桥之间需要切换时，不能简单地把原来工作着的一组桥的触发脉冲立即封锁，而同时把原来封锁着的另一组桥立即开通，因为已导通的晶闸管并不能在触发脉冲取消的那一瞬间立即被关断，必须待晶闸管承受反压时才能关断。如果对两组桥的触发脉冲的封锁和开放是同时进行的，原先导通的那组桥不能立即关断，而原先封锁着的那组桥反而已经开通，出现两组桥同时导通的情况，因没有环流电抗器，将会产生很大的短路电流，把晶闸管烧毁。为此首先应使已导通桥的晶闸管断流，要妥当处理主电路内电感储存的电磁能量，使其以续流的形式释放，通过原工作桥本身处于逆变状态，把电感储存的一部分能量回馈给电网，其余部分消耗在电动机上，直到储存的能量释放完，主电路电流变为零，使原导通晶闸管恢复阻断能力，随后再开通原封锁桥的晶闸管，使其触发导通。这种无环流可逆系统中，变流器之间的切换过程是由逻辑单元控制的，称为逻辑控制无环流系统。