矩阵变频电路的工作原理及输出条件分析

图5-38a是矩阵式变频电路的主电路拓扑。三相输入电压为u_a、u_b、u_c，三相输出电压为u_u、u_v、u_w。9个开关器件组成3×3矩阵，因此该电路称为矩阵式变频电路（Matrix Fre-quency Converter，MFC），也称为矩阵变换器。图中每个开关都是矩阵中的一个元素，采用双向可控开关，图5-38b给出了应用较多的一种开关单元。

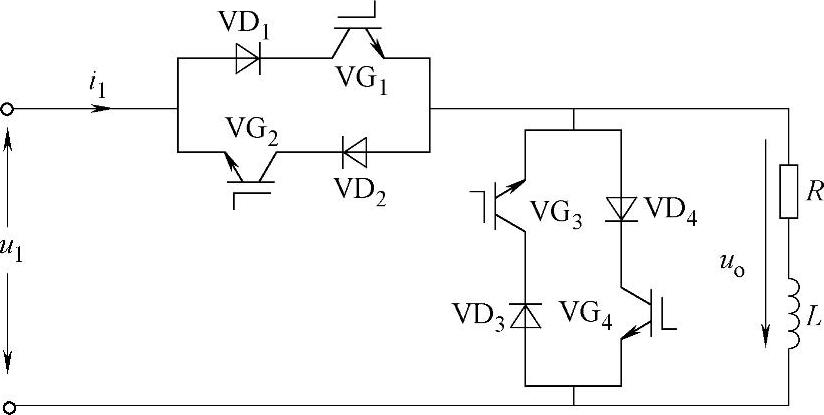
图5-36 斩控式交流调压电路

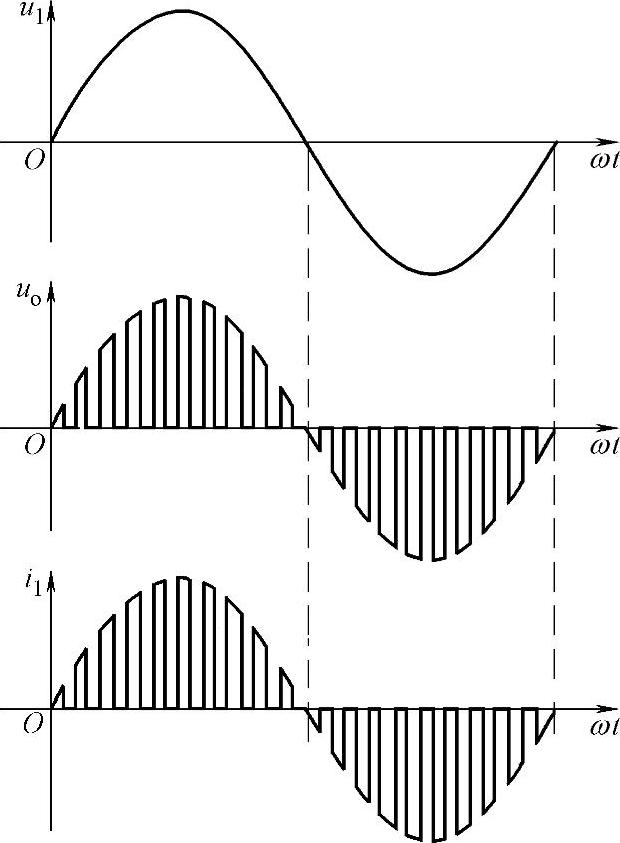
图5-37 电阻负载斩控式交流调压电路波形

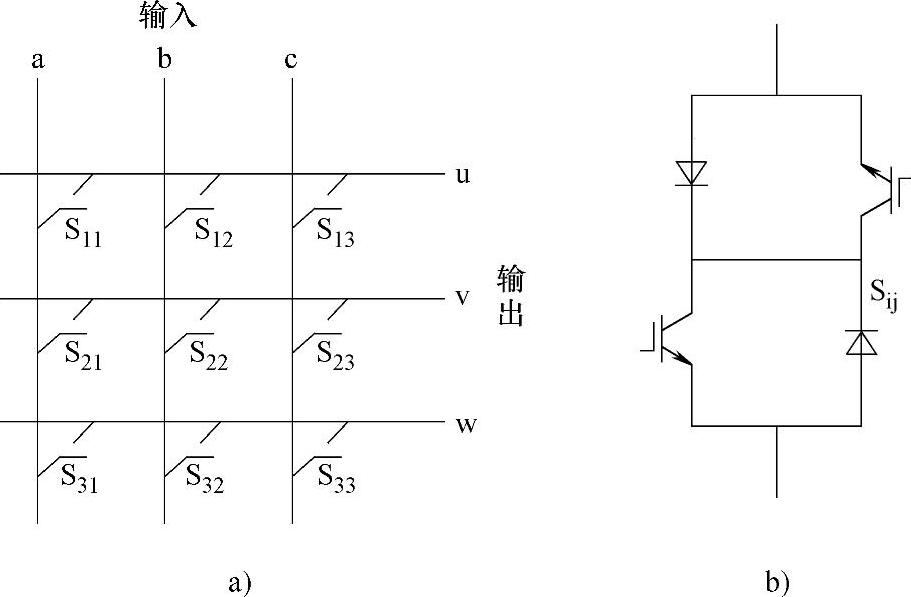
图5-38 矩阵式变频电路

矩阵式变频电路的优点是输入电流可控制为正弦波且和电压同相，功率因数为1，也可控制为需要的功率因数；其输出电压也为正弦波，输出频率不受电网频率的限制；能量可双向流动，适用于交流电动机的四象限运行；不通过中间直流环节而直接实现变频，效率较高。

下面来分析矩阵式变频电路的基本工作原理。

对单相交流电压u_s进行斩波控制，即进行PWM控制，如果开关频率足够高，则其输出电压u_o为

式中，T_c为开关周期；t_on为一个开关周期内开关的导通时间；α为占空比。

在不同的开关周期中采用不同的α可得到与u_s频率和波形都不同的u_o。由于单相交流电压u_s波形为正弦波，可利用的输入电压部分只有如图5-39a所示的单相电压阴影部分，因此输出电压u_o可能得到的波形也受其局限。如果把输入交流电源改为三相，例如用图5-38a中第一行的3个开关S₁₁、S₁₂、S₁₃共同作用来构造u相输出电压u_u，就可利用图5-39b的三相相电压包络线中所有的阴影部分，构造出所需要的输出电压。图5-39a、b用阴影部分示出了在单相输入和三相输入时，为构造输出电压可利用的输入电压部分。

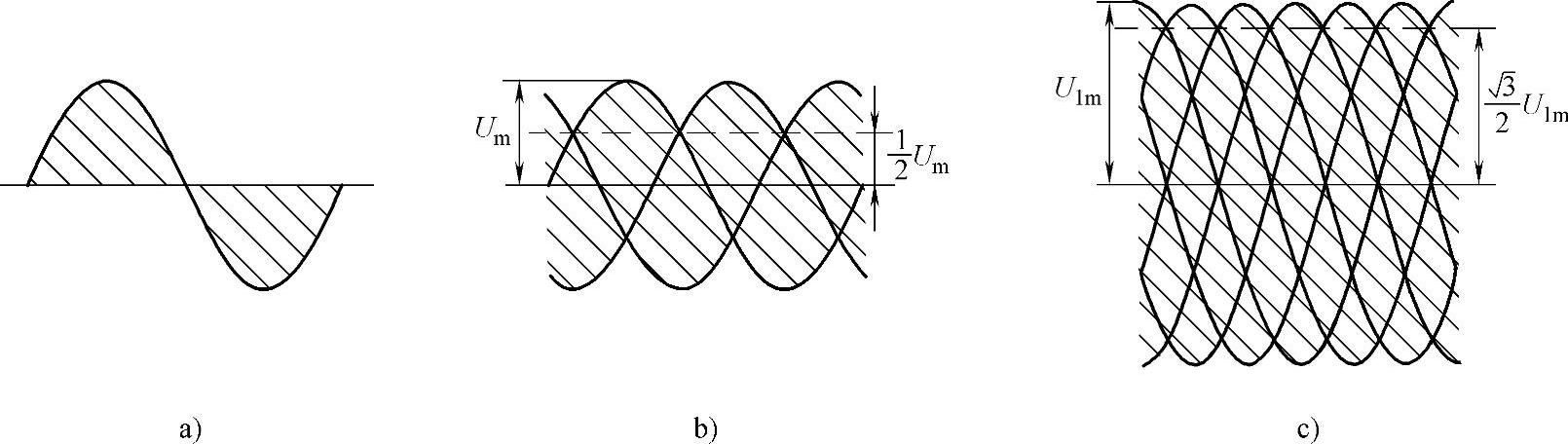
a）单相输入 b）三相输入相电压构造输出相电压 c）三相输出线电压构造输出线电压

图5-39 构造输出电压时可利用的输入电压部分

从图中可以看出，理论上所构造的u_u的频率可不受限制，但如u_o必须为正弦波，则其最大幅值仅为输入相电压u_a幅值的1/2。如果利用输入线电压来构造输出线电压，例如用图5-38a中第一行和第二行的6个开关共同作用来构造输出线电压u_uv，就可利用图5-39c中6个线电压包络线中所有的阴影部分。这样，当u_uv必须为正弦波时，其最大幅值就可达到输入线电压幅值的86.6%。这也是正弦波输出条件下矩阵式变频电路理论上最大的输出输入电压比。下面为了叙述方便，仍以相电压输出方式为例进行分析。

利用对开关S₁₁、S₁₂、S₁₃的控制构造输出电压u_u时，为了防止输入电源短路，在任何时刻只能有一个开关接通。考虑到负载一般是阻感负载，负载电流具有电流源的性质。为使负载不致开路，在任一时刻必须有一个开关接通。因此，u相输出电压u_u和各相输入电压的关系为

u_u=α₁₁u_a+α₁₂u_b+α₁₃u_c （5-61）

式中，α₁₁、α₁₂、α₁₃为一个开关周期内开关S₁₁、S₁₂、S₁₃的导通占空比。

由上面的分析可知

α₁₁+α₁₂+α₁₃=1 （5-62）

用同样的方法控制图5-38a矩阵第2行和第3行的各开关，可以得到类似于式（5-62）的u_v、u_w表达式。把这些公式合写成矩阵的形式，即

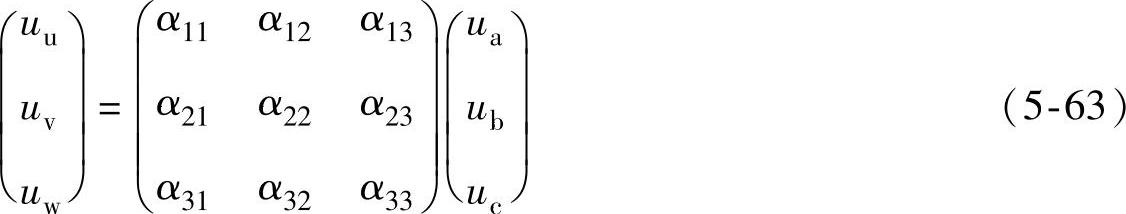
可缩写为

u_o=αu_i（5-64）

式中

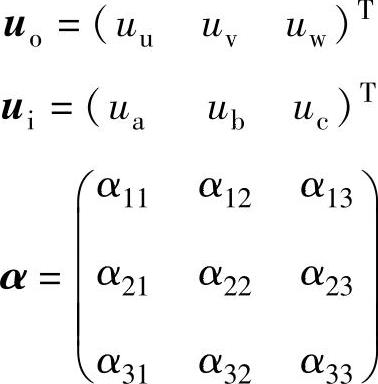
将α称为调制矩阵，它是时间的函数，每个元素在每个开关周期中都是不同的。

前已述及，阻感负载的负载电流具有电流源的性质，负载电流的大小是由负载的需要决定的，在矩阵式变频电路中，9个开关的通断情况决定后，即α矩阵中各元素确定后，输入电流i_a、i_b、i_c和输出电流i_u、i_v、i_w的关系也就确定了。实际上，各相输入电流都分别是各相输出电流按照相应的占空比相加而成的，即

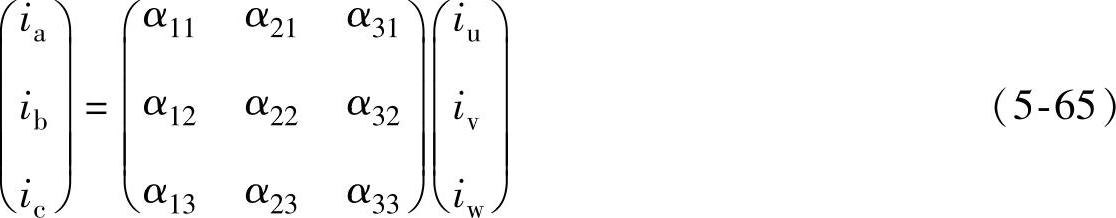(www.xing528.com)

可缩写为

i_i=α^Ti_o （5-66）

式中

i_i=[i_ai_bi_c]^T

i_o=[i_ui_vi_w]^T

式（5-64）、式（5-65）即是矩阵式变频电路的基本输入输出关系式。

对一个实际系统来说，输入电压和所需要的输出电流是已知的，设其分别为

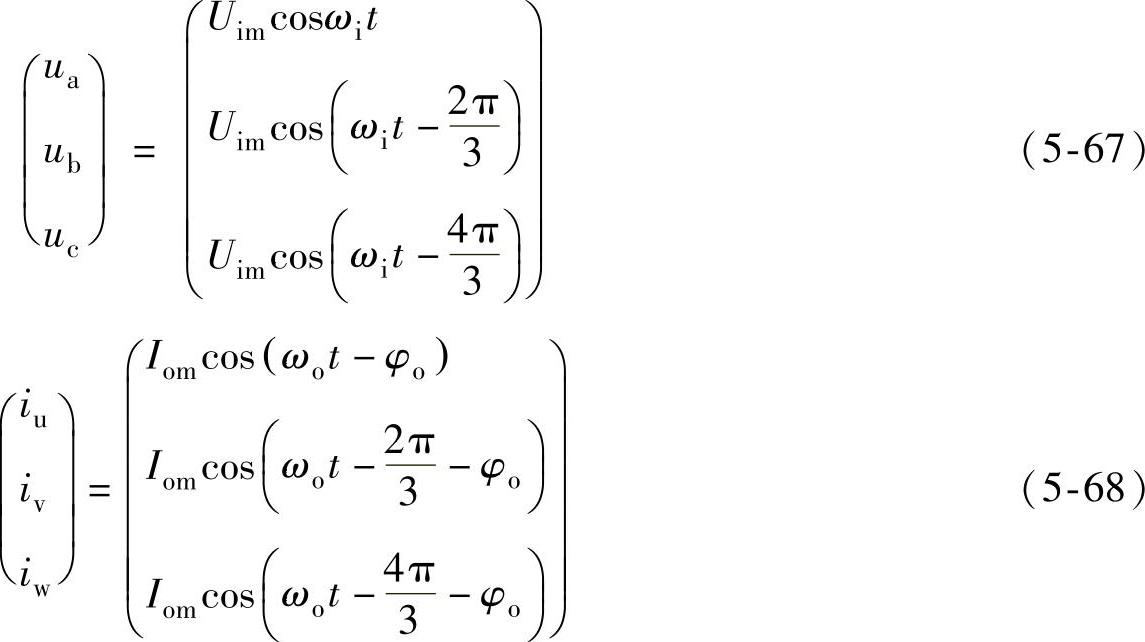
式中，U_im、I_om为输入电压和输出电流的幅值；ω_i、ω_o为输入电压和输出电流的角频率；φ_o为相应于输出频率的负载阻抗角。

变频电路希望的输出电压和输入电流分别为

式中，U_om、I_im为输出电压和输入电流的幅值；φ_i为输入电流滞后电压的相位角。

当期望的输入功率因数为1时，φ_i=0。把式（5-66）～式（5-69）代入式（5-62）和式（5-64），可得

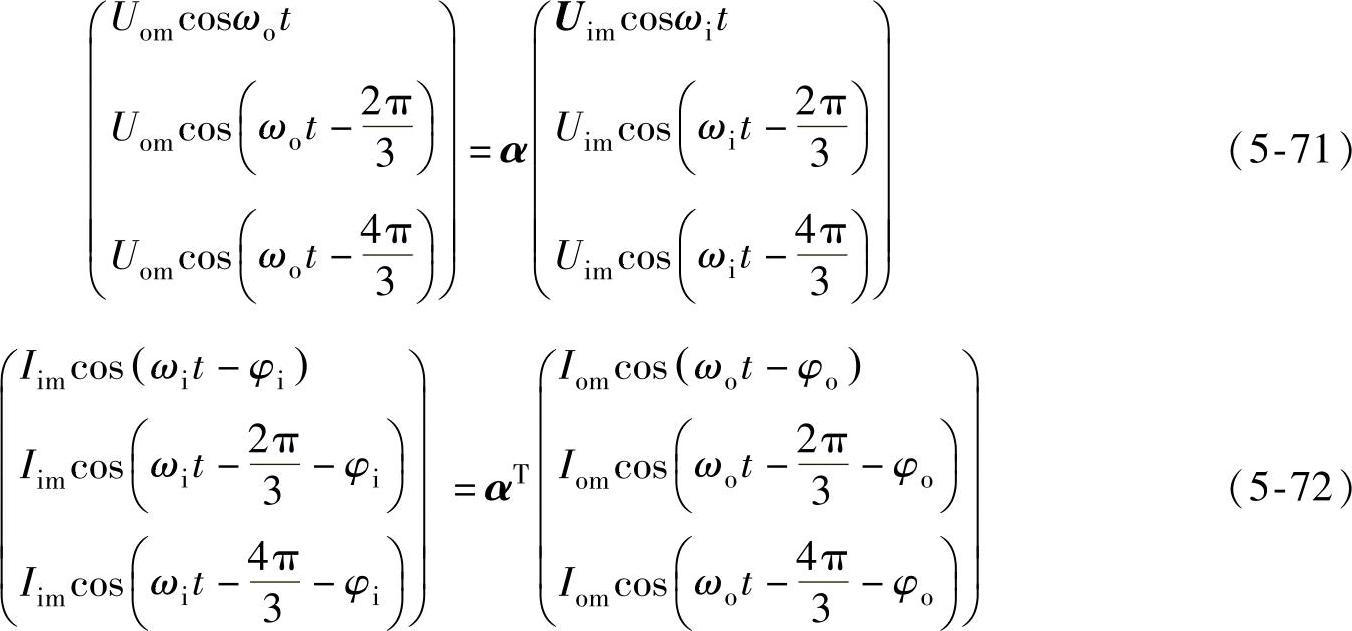
如能求解满足式（5-70）和式（5-71）的调制矩阵α，就可得到式中所希望的输出电压和输入电流。但是，这种求解是十分困难的，而且满足方程的解可以有许多。通过对电路工作原理的分析可知，调制矩阵α应满足以下条件：

1）α_ij应具有正弦函数的性质，且其角频率应该和输入角频率ω_i及输出角频率ω_o均有关。

2）因为三相输入和输出电压、电流均对称，因此构成矩阵中任一行或列的元素项均有相位相差2π/3。

3）为保证输入电源不短路，且负载电流不断流，任一时刻α矩阵对应的同一行的矩阵开关元件只能有一个导通且必须有一个导通。因此有

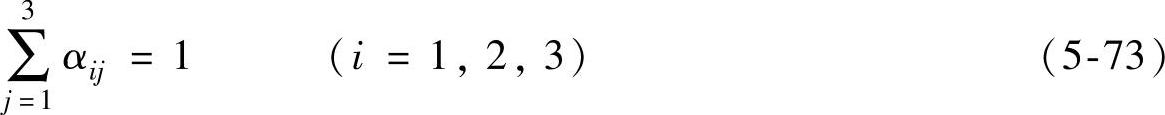
满足上述条件的α_1j的一种形式为

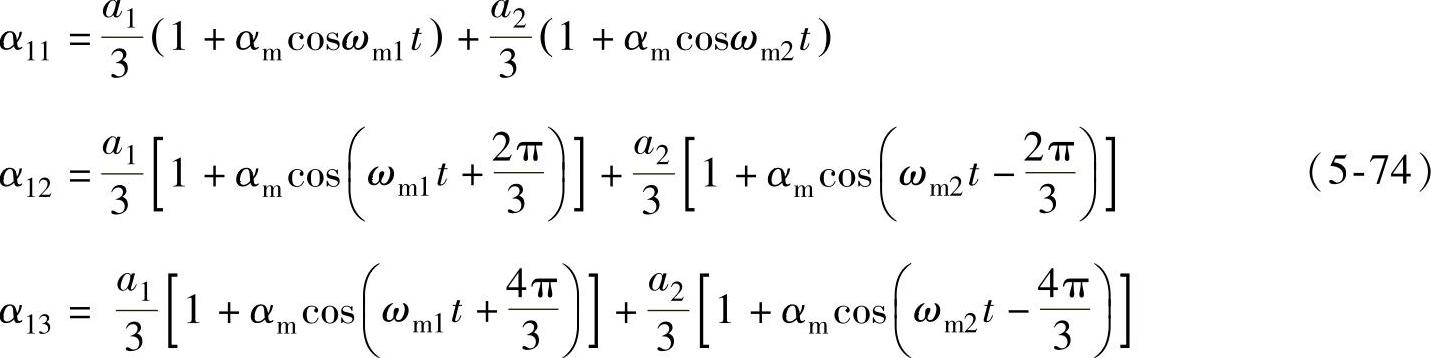
式中，a₁=（1+tanφ_icosφ_o）/2；a₁+a₂=1；α_m为电压传输率，α_m=U_om/U_im；ω_m1=ω_i-ω_o；ω_m2=ω_i+ω_o。

可以看出，当要求输入功率因数为1，即φ_i=0时，a₁=a₂=1/2。

将式（5-73）代入式（5-71）的第一行可求得

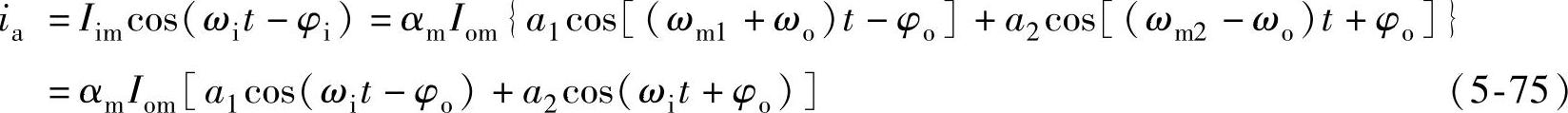
调整a₁和a₂，就可以改变φ_i，得到所希望的输入功率因数，例如可使输入电流超前电压，向电网提供无功功率。一般来说，希望功率因数为1，φ_i=0，这时a₁=a₂=0.5，代入式（5-74）可得

I_imcosω_it=α_mI_omcosφ_ocosω_it （5-76）

这一结果说明，利用式（5-73）所给出的调制函数可以使输入电流为正弦波，且和电压同相位，功率因数为1。从电压传输率的角度看，该函数不是最佳形式，其最大传输率仅为1/2。采用其他方法可以得到较高的电压传输率。

从上面的分析可以看出，矩阵式变频电路的缺点是电路结构较复杂，每个电路至少要用18个全控型器件，每个器件还要并联一个二极管，另外控制也很复杂。因此，这种电路目前还未进入实用阶段。但是这种电路也有十分突出的优点，它可使输出电压呈现正弦波形，输出频率不受输入频率限制；输入电流呈现正弦波形，可与输入电压同相位，即输入功率因数为1，也可控制为所需功率因数；能量可双向流动，适合于交流电动机的四象限运行；直接实现变频，无中间直流环节及滤波元件，变换效率高。因此它是一种电气性能十分优良、极具应用前景的频率变换电路，对它的研究、学习具有深远的学术意义和潜在的应用价值；矩阵式变频器在变频调速中的应用研究既可产生节能的重大经济效益，又避免了因谐波污染带来的电力系统环保问题，是一种“绿色”的变换器。随着研究的不断深入，电力电子器件和应用技术以及微机控制技术的发展，控制理论的日益完善，成本的不断降低，矩阵式变频器必将以其独特的优点在未来产品化方面形成优势，日益接近实用化。