三相输入单相输出交-交变频器技术简析

1.电路构成和基本工作原理

图5-13是单相交-交变频电路的基本原理图和输出电压波形。电路由P组和N组反并联的晶闸管变换电路构成，和直流电动机可逆调速用的四象限变流电路完全相同。变换器P和N都是相控整流电路，P组工作时，负载电流为正，N组工作时，负载电流为负。让两组变换器按一定的频率交替工作，负载就得到该频率的交流电。改变两组变流器的切换频率，就可以改变输出频率ω₀。改变变频电路工作时的触发延迟角α，就可以改变交流输出电压的幅值。

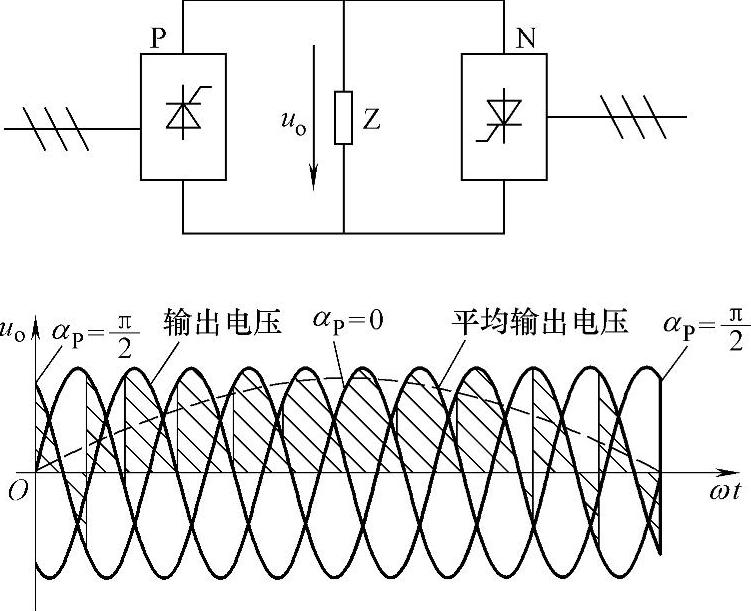
图5-13 单相交-交变频电路的基本原理图和输出电压波形

为了使输出电压u_o的波形接近正弦波，可以按正弦规律对α进行调制。如图5-13波形所示，可在半个周期内让正组变换器P的α按正弦规律从90°逐渐减小到0或某个值，然后再逐渐增大到90°。这样，每个控制间隔内的平均输出电压就按正弦规律从零逐渐增至最高，再逐渐减低到零，如图中虚线所示。另外半个周期可对变换器N进行同样的控制。

图5-13所示波形是变换器P和N都是三相半波相控电路时的波形。可以看出，输出电压u_o并不是平滑的正弦波，而是由若干段电源电压拼接而成。在输出电压的一个周期内，所包含的电源电压段数越多，其波形就越接近正弦波。因此，图5-13中的变换电路通常采用6脉波的三相桥式电路或12脉波变换电路。本节在后面的论述中均以最常用的三相桥式电路为例进行分析。

2.整流与逆变工作状态

交-交变频电路的负载可以是阻感负载、电阻负载、阻容负载或交流电动机负载。这里以阻感负载为例来说明电路的整流工作状态与逆变工作状态，这种分析也适用于交流电动机负载。

如果把交-交变频电路理想化，忽略变换电路换相时输出电压的脉动分量，就可把电路等效成图5-14a所示的正弦波交流电源和二极管的串联。其中交流电源表示变换电路可输出交流正弦电压，二极管体现了电流的单向流动特征，负载Z为感性，负载阻抗功率因数角为φ。另外，两组变换电路在工作时采取直流可逆调速系统中的无环流工作方式，即一组变换电路工作时，封锁另一组变换电路的触发脉冲。

图5-14b所示为一个周期内负载电压u_o、负载电流i_o波形及正反两组变流电路的电压u_P、u_N和电流i_P、i_N波形。由于变换电路的单向导电性，在t₁～t₃期间的负载电流正半周，只能是正组变换电路工作，反组电路被封锁。其中在t₁～t₂阶段，输出电压和电流均为正，故正组变换电路工作在整流状态，输出功率为正。在t₂～t₃阶段，输出电压已反向，但输出电流仍为正，正组变换电路工作在逆变状态，输出功率为负。

在t₃～t₅阶段，负载电流负半周，反组变换电路工作，正组电路被封锁。其中在t₃～t₄阶段，输出电压和电流均为负，反组变换电路工作在整流状态，在t₄～t₅阶段，输出电流为负而电压为正，反组变换电路工作在逆变状态。

可以看出，在阻感负载的情况下，在一个输出电压周期内交-交变频电路有4种工作状态。哪组变换电路工作是由输出电流的方向决定的，与输出电压极性无关。变换电路工作在整流状态还是逆变状态，则是根据输出电压方向与输出电流方向是否相同来确定的。

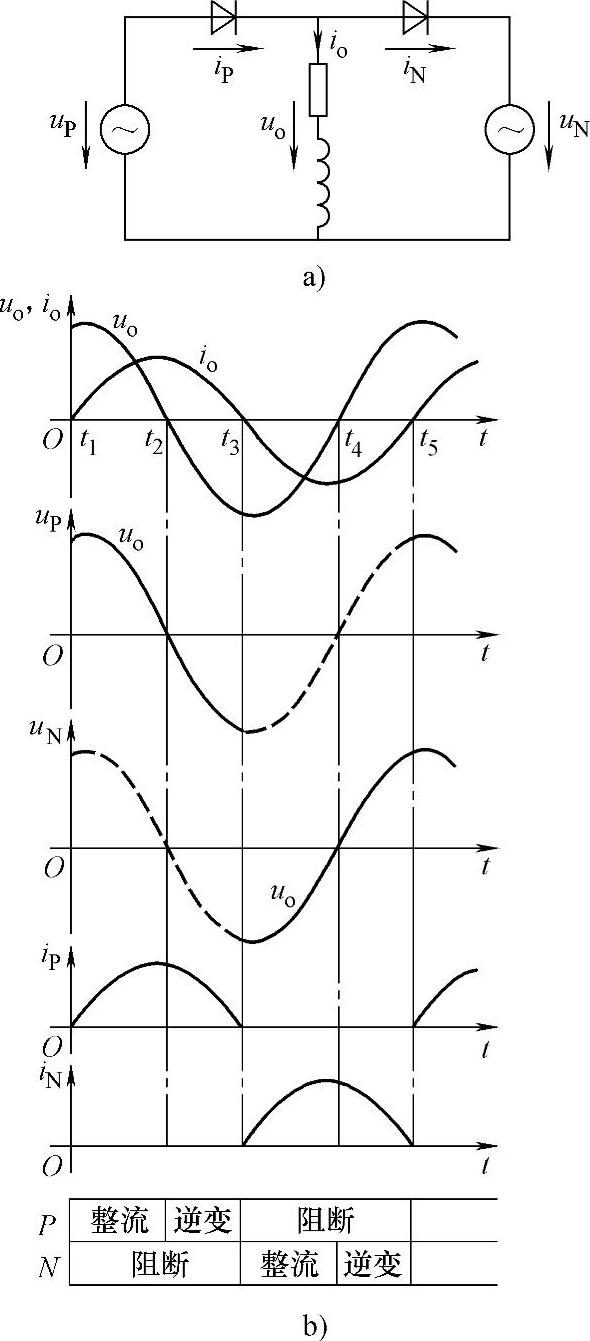
图5-14 理想化交-交变频电路的整流和逆变工作状态

图5-15是单相交-交变频电路输出电压和电流波形。如果考虑到无环流工作方式下负载电流过零的死区时间，一周期的波形可分为6段，第1段i_o＜0，u_o＞0，为反组逆变；第2段电流过零，为无环流死区；第3段i_o＞0，u_o＞0，为正组整流；第4段i_o＞0，u_o＜0，为正组逆变；第5段又是无环流死区；第6段i_o＜0，u_o＜0，为反组整流。

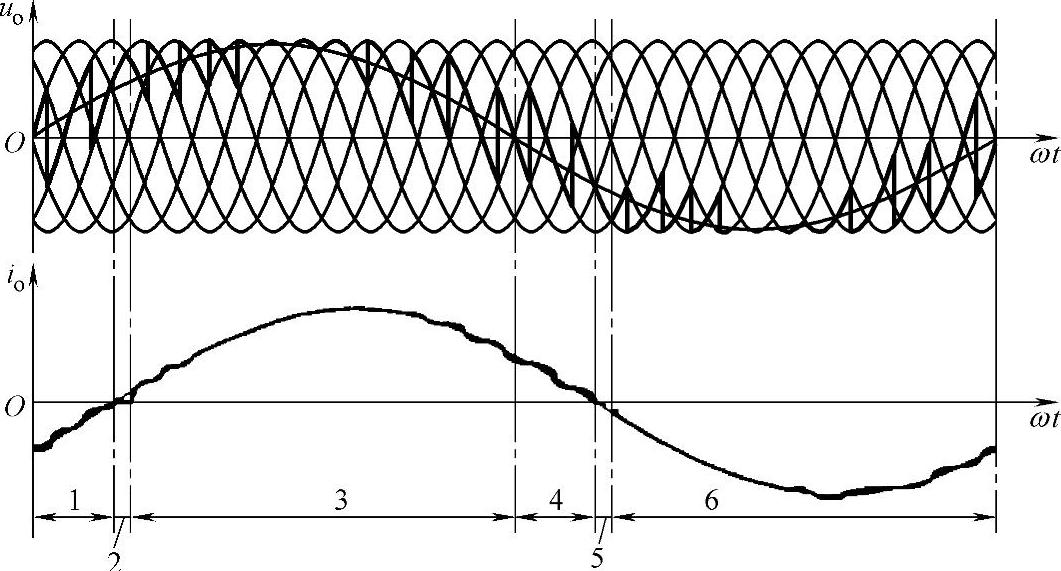
图5-15 单相交-交变频电路输出电压和电流波形

当输出电压和电流的相位差φ＜90°时，一周期内电网向负载提供能量的平均值为正，电动机工作在电动状态；当二者相位差φ＞90°时，一周期内电网向负载提供能量的平均值为负，即电网吸收能量，电动机工作在发电状态；如果φ=0，负载功率因数cosφ=1，输出电压、电流同向，第1及第4区域不存在；如果φ=π，负载功率因数cosφ=-1，输出电压、电流反向，第3及第6区域不存在。

3.输出正弦波电压的调制方法

使交-交变频电路的输出电压波形基本为正弦波的调制方法有很多，这里主要介绍最基本的、广泛使用的余弦交点法。

设U_d0为α=0时整流电路的理想空载电压，晶闸管变流器输出电压为

对交-交变频电路来说，每次控制时α都是不同的，式（5-13）中的u_o表示每次控制间隔内输出电压的平均值。

设要得到的正弦波输出电压为

u_o=U_omsinω₀t （5-15）

比较式（5-13）和式（5-14）可得

(www.xing528.com)

式中，γ称为输出电压比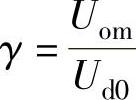，（0≤γ≤1），因此

α=arccos（γsinω₀t） （5-17）

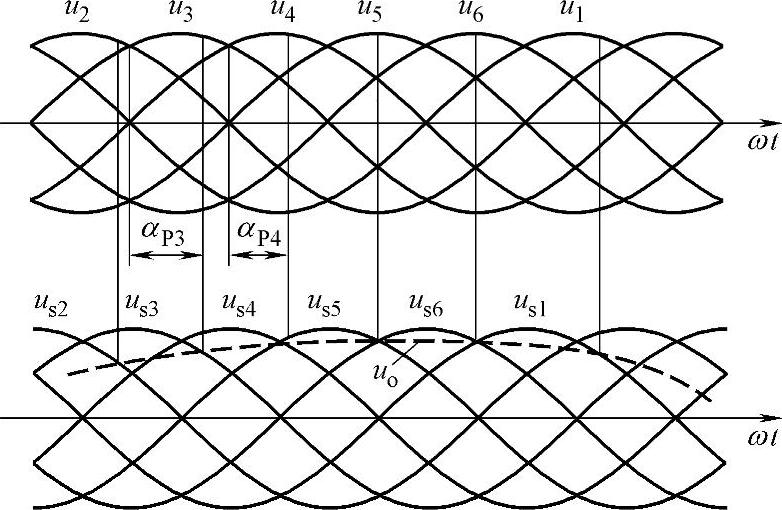
图5-16 余弦交点法原理

式（5-16）就是用余弦交点法求交-交变频电路α的基本公式。

下面用图5-16对余弦交点法作进一步说明。图5-16中，电网线电压u_ab、u_ac、u_bc、u_ba、u_ca、u_cb依次用u₁～u₆表示，相邻两个线电压的交点对应于α=0。u₁～u₆所对应的同步余弦信号分别用u_s1～u_s6表示。u_s1～u_s6比相应的u₁～u₆超前30°。也就是说，u_s1～u_s6的最大值正好和相应线电压α=0的时刻相对应，如以α=0为零时刻，则u_s1～u_s6为余弦信号。设希望输出的电压为u_o，则各晶闸管的触发时刻由相应的同步电压u_s1～u_s6的下降段和u_o的交点来决定。

图5-17给出了在不同输出电压比γ的情况下，输出电压的一个周期内，触发延迟角α随ω₀t变化的情况。可以看出，当γ较小，即输出电压较低时，α只在离90°很近的范围内变化，电路的输入功率因数非常低。

上述余弦交点法可以用模拟电路来实现，但电路复杂，且不易实现准确的控制。采用计算机控制时可方便地实现准确的运算，而且除计算α外，还可以实现各种复杂的控制运算，使整个系统获得很好的性能。

4.输入输出特性

（1）输出上限频率

交-交变频电路的输出电压是由许多段电网电压拼接而成的。一个输出周期内拼接的电网电压段数越多，输出电压波形越接近正弦。当输出频率增高时，输出电压一周期所含电网电压的段数就减少，波形畸变就严重。电压波形畸变以及由此产生的电流波形畸变和转矩脉动是限制输出频率提高的主要因素。就输出波形畸变和输出上限频率的关系而言，很难确定一个明确的界限。当然，构成交-交变频电路的两组变换电路的脉波数越多，输出上限频率就越高。就常用的6脉波三相桥式电路而言，一般认为，输出上限频率不高于电网频率的1/3～1/2。电网频率为50Hz时，交-交变频电路的输出上限频率约为20Hz。

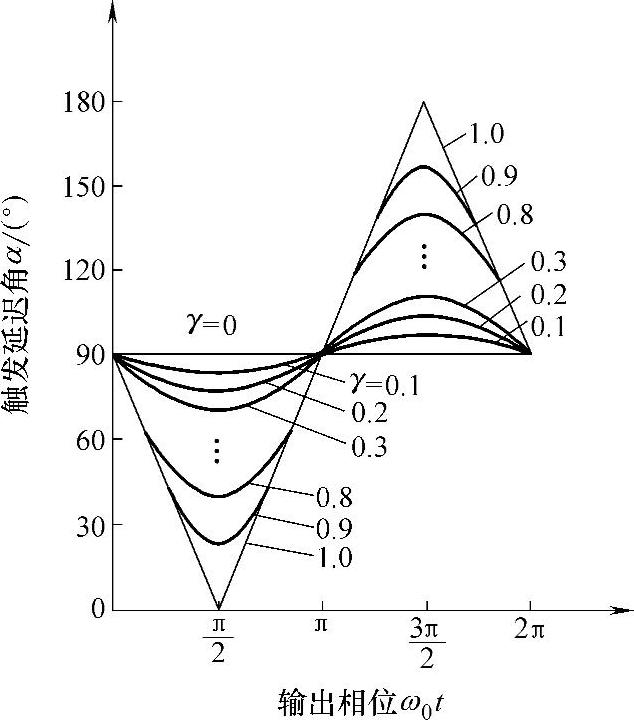
图5-17 不同γ时α和ω₀t的关系

（2）输入功率因数

交-交变频电路采用的是相位控制方式，因此其输入电流的相位总是滞后于输入电压，需要电网提供无功功率。从图5-17可以看出，在输出电压的一个周期内，α是以90°为中心而前后变化的。输出电压比γ越小，半周期内α的平均值越靠近90°，功率因数越低。另外，负载的功率因数越低，输入功率因数也越低。而且不论负载功率因数是滞后的还是超前的，输入的无功电流总是滞后的。

图5-18给出了以输出电压比γ为参变量时输入功率因数和负载功率因数的关系。输入功率因数也就是输入的基波功率因数，其值通常略大于输入功率因数。因此，图5-18也大体反映了输入功率因数和负载功率因数的关系。可以看出，即使负载功率因数为1且输出电压比γ也为1，输入功率因数仍小于1，随着负载功率因数的降低和γ的减小，输入功率因数也随之降低。

（3）输出电压谐波

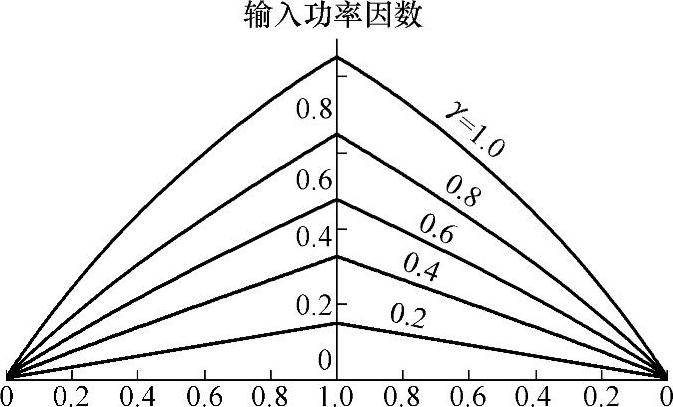
图5-18 单相交-交变频电路的功率因数

交-交变频电路输出电压的谐波成分非常复杂，和输入频率f_i、输出频率f_o、电路脉波数均有关。采用三相桥式电路的交-交变频电路输出电压中的主要谐波频率为6f_i±f_o，6f_i±3f_o，6f_i±5f_o，…；12f_i±f_o，12f_i±3f_o，12f_i±5f_o，…；等等。另外，采用无环流控制方式时，由于电流方向改变时死区的影响，将使输出电压中增加5f_o、7f_o等次谐波。

（4）输入电流谐波

单相交-交变频电路的输入电流波形及幅值均按正弦规律被调制，和相控整流电路相比，其输出电流频谱要复杂得多，但各次谐波的幅值要比相控整流电路的谐波幅值小。采用三相桥式电路的单相交-交变频电路输入电流的谐波频率为

和 f_in=f_i±2kf_o （5-19）

式中，k=1，2，3，…；l=0，1，2，…。