多电平PWM整流器可分为钳位式多电平PWM整流器和级联式(包括多重化)多电平PWM整流器。本小节以中性点钳位式三电平PWM整流器为例来介绍多电平PWM整流器的基本原理。
根据中性点钳位式PWM逆变器在大功率领域的成功应用和PWM整流器在提高电能质量方面的优良表现,促使人们将中性点钳位式电路结构移植到PWM整流器中,图3-103是中性点钳位式三相三电平PWM整流器的主电路,由图可见,它只是电源与负载对调,即电源是三相交流电网,负载是有源或无源直流负载(图示为Rd-Ld串联无源直流负载)。直流输出端分压电容C1=C2,其端压Ud1=Ud2=Ud/2,O′为直流输出中性点。VDS1~VDS6为钳位二极管,其接法与中性点钳位式PWM逆变电路NPC-INV相仿。
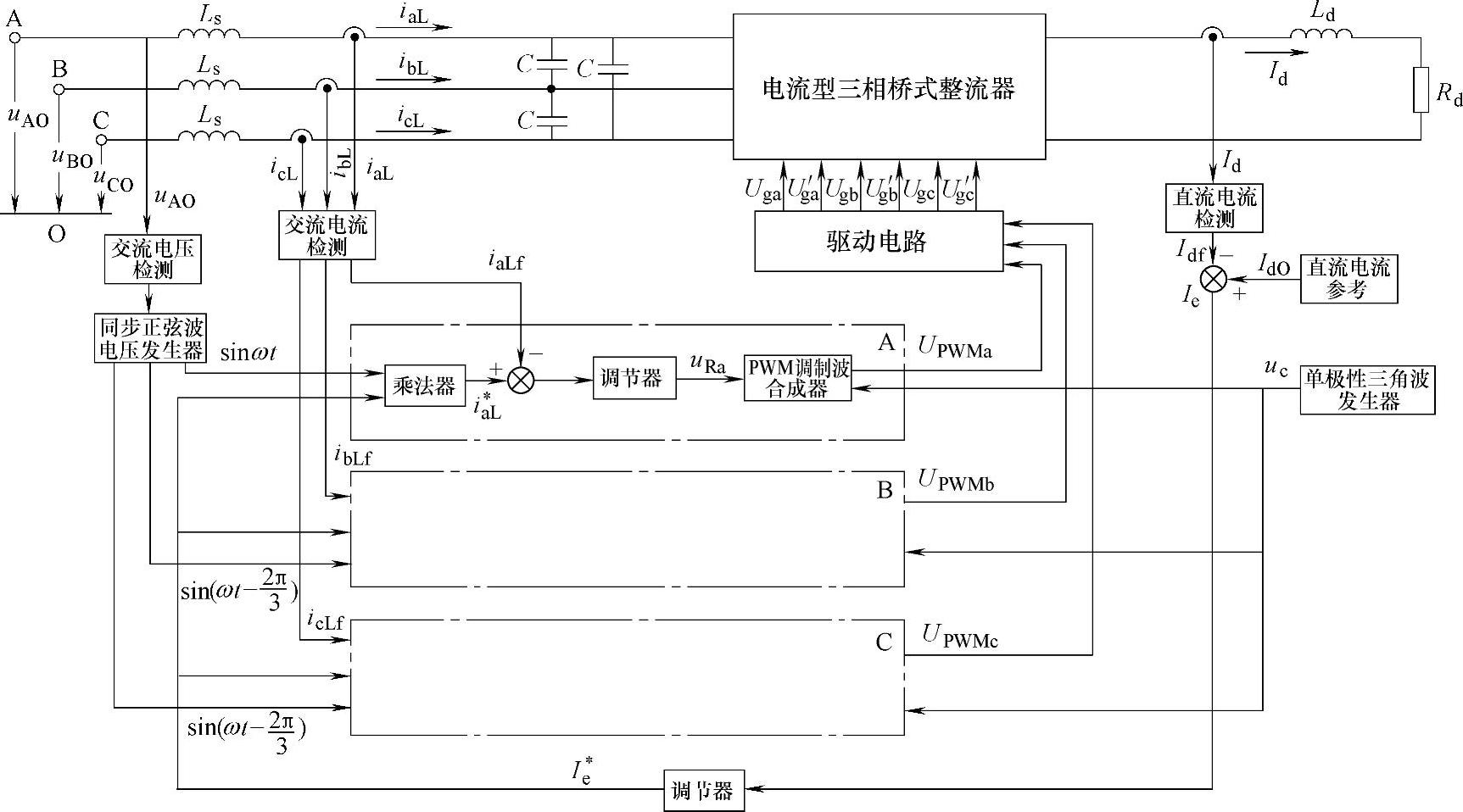
图3-102 电流型三相桥式PWM整流器框图
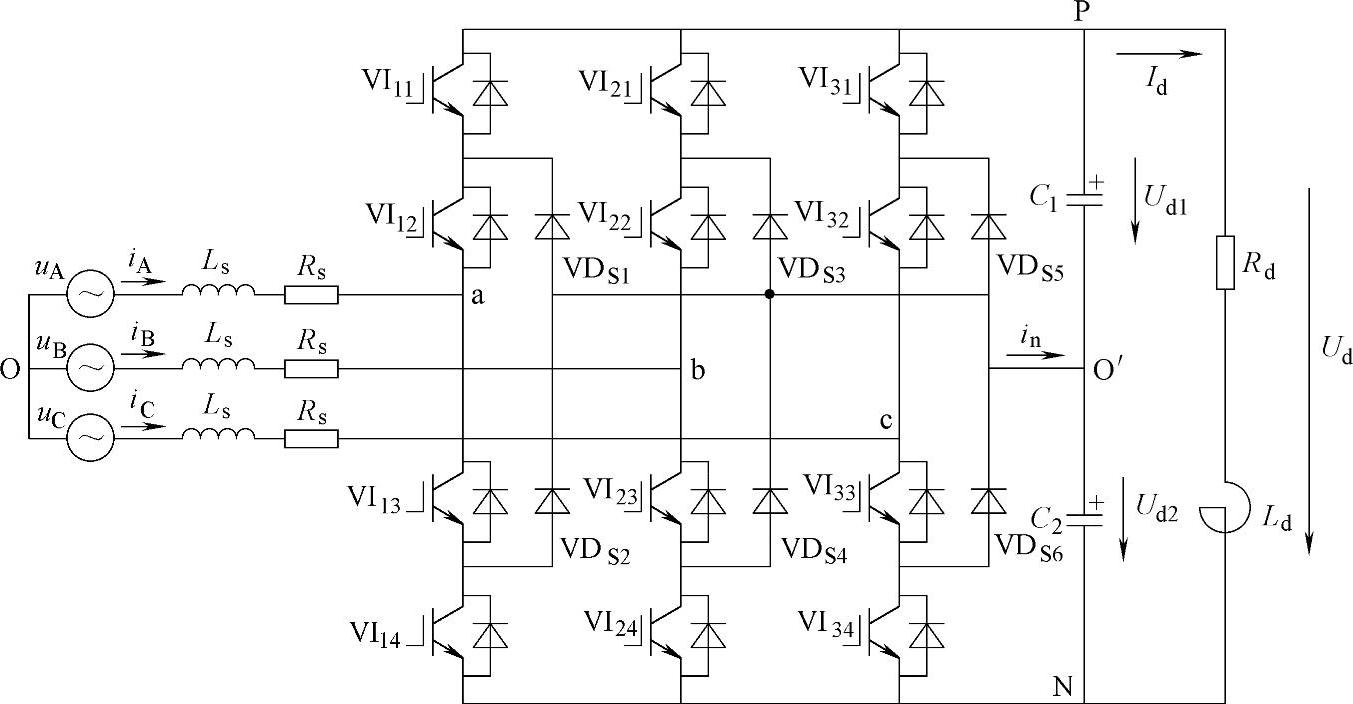
图3-103 中性点钳位式三相三电平PWM整流器的主电路
由于空间电压矢量PWM控制(SVPWM)具有直流利用率高、开关次数少和易于实现全数字化控制等优点,故在中性点钳位式多电平PWM整流器中得到了广泛应用。
1.SVPWM的控制方法
与NPC-INV相同,由于每相对直流中性点均有三种电平(代表电路的三种开关状态),因此三相桥共有27个开关状态,其在α-β坐标系中的分布如图3-104a所示,由图可见,这些电压矢量的组成是:
1)零矢量(3个):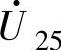 (PPP)、
(PPP)、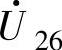 (NNN)和
(NNN)和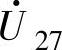 (CCC)。
(CCC)。
2)非零矢量(24个):包含长、中、短幅值三种矢量,长矢量指幅值为2Ud/3的矢量,属于这类矢量的有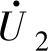 、
、 、
、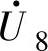 、
、 、
、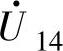 和
和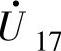 共6种;中矢量指幅值为
共6种;中矢量指幅值为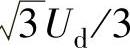 的矢量,属于此类矢量的有
的矢量,属于此类矢量的有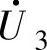 、
、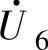 、
、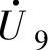 、
、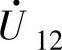 、
、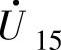 和
和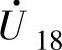 共6种;短矢量则指幅值为Ud/3的矢量,属于此类矢量的有6对12种,如
共6种;短矢量则指幅值为Ud/3的矢量,属于此类矢量的有6对12种,如 和
和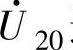 这对矢量不仅幅值相等,且相位相同,与此相仿的还有
这对矢量不仅幅值相等,且相位相同,与此相仿的还有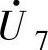 和
和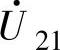 、
、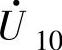 和
和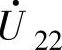 、
、 和
和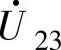 、
、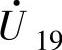 和
和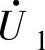 、
、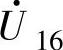 和
和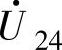 。
。
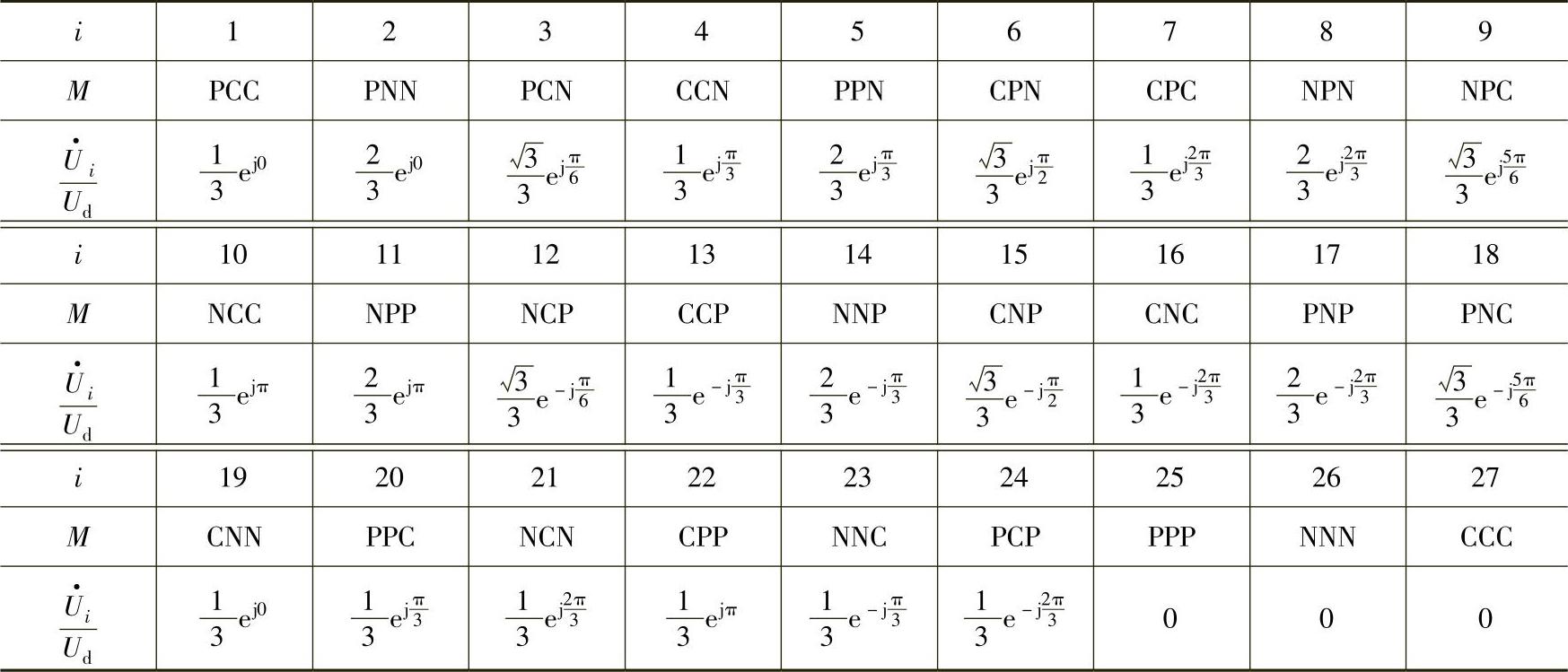
上述矢量所代表的电路开关状态见表3-7,如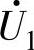 所对应的状态为PCC,
所对应的状态为PCC,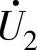 为PNN等。
为PNN等。
表3-7 NPC-REC电压空间矢量所代表的电路开关状态
将24个非零矢量的分布划分为Ⅰ-Ⅵ六个扇形区,与两电平电路相仿,为减少电流谐波含量,用多个非零矢量去逼近指定电压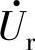 ,为此将每个扇区再细分为A~D四个子扇区,以第Ⅰ扇区为例如图3-104b所示,图中三角形子区D拥有
,为此将每个扇区再细分为A~D四个子扇区,以第Ⅰ扇区为例如图3-104b所示,图中三角形子区D拥有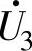 、
、 和
和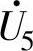 三个空间矢量(如三角形各顶点所标)。余类推。
三个空间矢量(如三角形各顶点所标)。余类推。
与NPC-SVPWM-INV相仿,NPC-SVPWM-REC的控制算法包含:①各电压矢量作用时间的计算;②指令值矢量的计算;③采样信号坐标系统的换算。下面先讨论作用时间的计算,其他的将在控制电路中讨论。
设指令电压矢量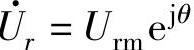 落在图3-104b的B子区中并可用电压矢量
落在图3-104b的B子区中并可用电压矢量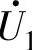 、
、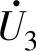 和
和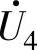 的分量
的分量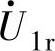 、
、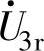 和
和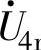 来逼近,仿照SVPWM控制的调频原理可得
来逼近,仿照SVPWM控制的调频原理可得
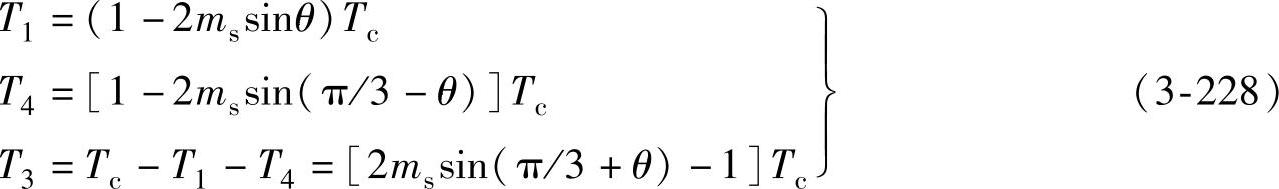
式中T1、T3和T4分别是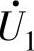 、
、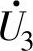 和
和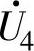 的作用时间。调制比为
的作用时间。调制比为

由于输出电压Ud和开关周期Tc为恒值,因此只要知道Urm和θ便可由式(3-228)确定各作用时间。
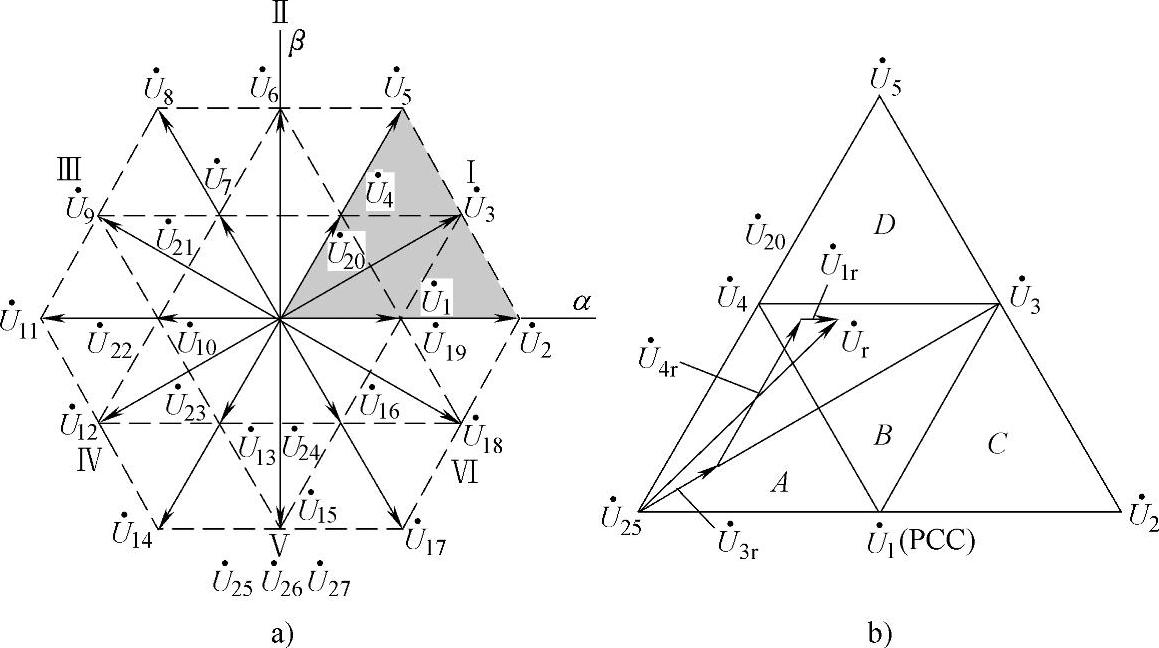
图3-104 NPC-REC中电压空间矢量的分布
a)在α-β坐标轴上的分布 b)子区分布
2.NPC-SVPWM-REC的控制
采用SVPWM控制方案的NPC-REC系统结构如图3-105所示,其中点画线框内为控制电路。与图3-96点画线框中的控制电路相比较有以下相同之处:
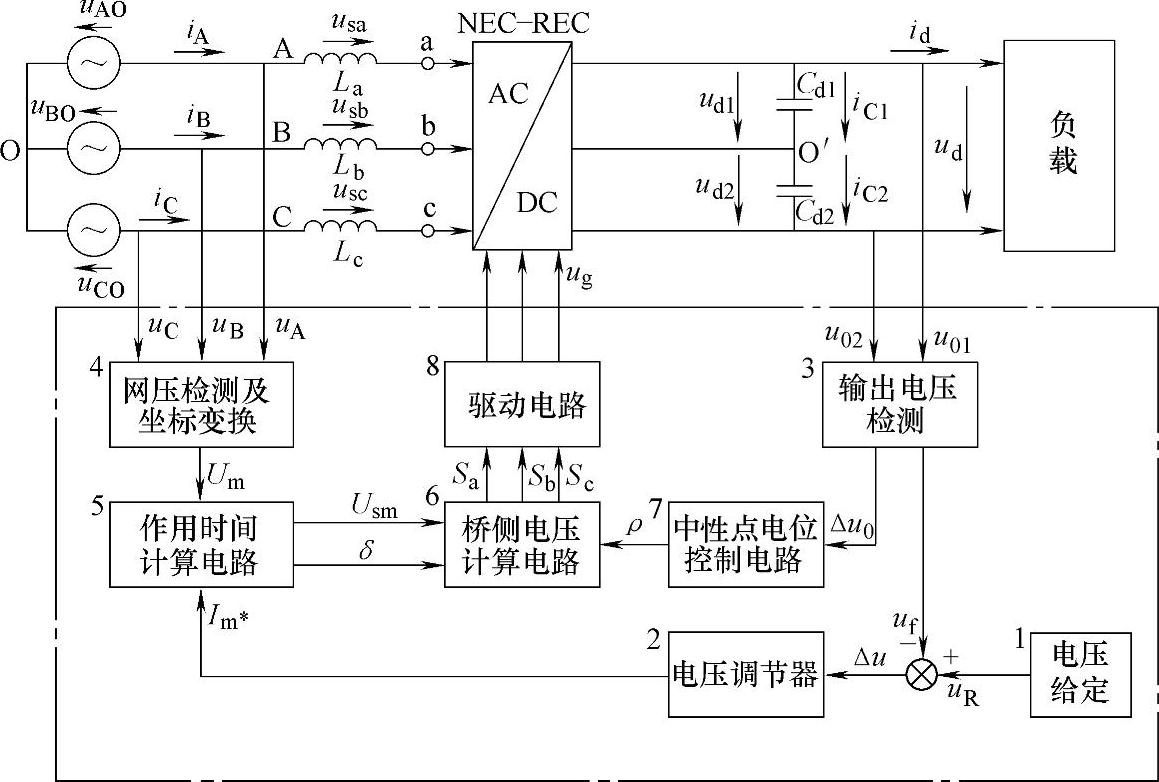
图3-105 采用SVPWM控制的NPC-REC系统结构
1)两个控制电路均采用电流间接控制策略。SVPWM方案本质上属于电流间接控制策略,因为它也是通过桥侧电压间接地实现对网侧电流的控制。(https://www.xing528.com)
2)两种控制电路都拥有一个电压外环,都是用PI调节器实现输出电压的调节。
3)两种控制电路均假定网侧基波相移角δ=0,也即交流侧的矢量关系如图3-96b所示。
但两种控制电路也存在下面不同之处:
在PWM信号生成方式上,图3-96采用的是SPWM方式;图3-105采用的则是SVPWM方式。下面对图3-105控制电路中的几个主要单元进行介绍。
(1)矢量作用时间计算单元5
电路的任务是根据输入指令电压的幅值和相角判断它在α-β坐标系中电压矢量分布的区域,并决定用哪些电压矢量去逼近它(如前述采用最近三角形法可取得较好效果),例如指令矢量落在图3-104b的子区B中,即用矢量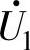 、
、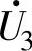 和
和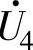 逼近,并按式(3-228)分别计算其作用时间T1、T3和T4。然后按中心对准方式安排其输出开关函数Sa、Sb和Sc的时序。
逼近,并按式(3-228)分别计算其作用时间T1、T3和T4。然后按中心对准方式安排其输出开关函数Sa、Sb和Sc的时序。
根据电流间接控制的原理,输入端指令电压应为桥侧基波电压,即

式中,δ是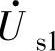 对网压矢量
对网压矢量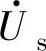 的相移角,设δ<0,即
的相移角,设δ<0,即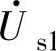 滞后于
滞后于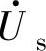 。
。
(2)桥侧电压矢量计算单元6由图3-105可见,计算单元5的输出是桥侧基波电压矢量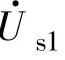 的幅值Usm及其相移角δ。在网侧相移角δ=0的条件下,根据式(3-216)和式(3-217),对于确定的输入电感Ls和电网角频率ω,只要网侧电流幅值Im和电网电压幅值Um为已知,即可计得Usm和δ。单元5有两个输入:一个是来自电压调节器的输出Im*,另一个是来自坐标变换单元4的输出Um。
的幅值Usm及其相移角δ。在网侧相移角δ=0的条件下,根据式(3-216)和式(3-217),对于确定的输入电感Ls和电网角频率ω,只要网侧电流幅值Im和电网电压幅值Um为已知,即可计得Usm和δ。单元5有两个输入:一个是来自电压调节器的输出Im*,另一个是来自坐标变换单元4的输出Um。
(3)检测和坐标变换单元4如图3-100所示,电网电压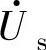 定向于d轴(其幅值为Um),在δ=0条件下,网侧电流矢量
定向于d轴(其幅值为Um),在δ=0条件下,网侧电流矢量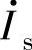 在q轴上的分量Isq=0,其d轴分量Isd=Im,取自电压调节器的输出。单元4的输入取自电网电压uAO、uBO和uCO,如果选择三相静止坐标系的原点,并以A相电压uAO定向于该坐标的a轴,则三相电网电压可表示为
在q轴上的分量Isq=0,其d轴分量Isd=Im,取自电压调节器的输出。单元4的输入取自电网电压uAO、uBO和uCO,如果选择三相静止坐标系的原点,并以A相电压uAO定向于该坐标的a轴,则三相电网电压可表示为
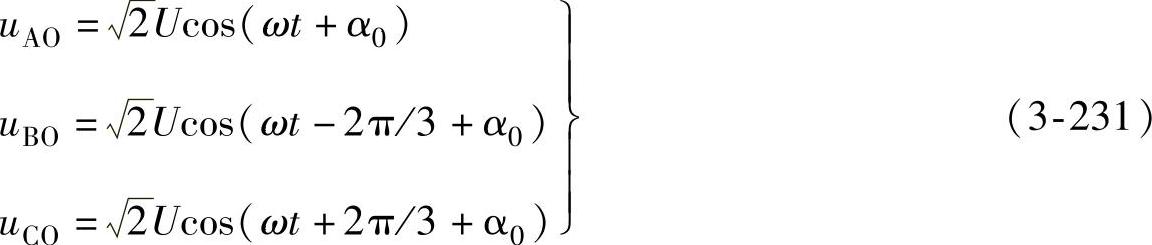
其合成空间矢量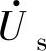 可表示为
可表示为
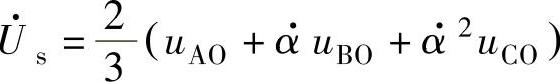
将式(3-231)代入上式可得
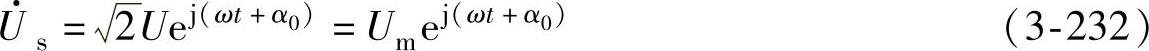
矢量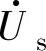 在α-β坐标轴的分量分别为
在α-β坐标轴的分量分别为

矢量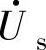 在d-q坐标轴的分量分别为
在d-q坐标轴的分量分别为

α-β坐标系和d-q坐标系的关系如图3-106所示。图中φ=ωt,即φ随时间t而变。但α0不变,因为φ和d-q坐标系都以角频率ω同步旋转。若重新选择时间坐标原点使α0=0,则有
Usd=Um,Usq=0 (3-237)
即将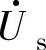 定向于旋转坐标系的d轴,于是整流器交流侧的矢量关系仍如图3-100b所示。综上所述,单元4的输出应为α0=0时,定向于d轴上的电网电压,其幅值仍为Um。
定向于旋转坐标系的d轴,于是整流器交流侧的矢量关系仍如图3-100b所示。综上所述,单元4的输出应为α0=0时,定向于d轴上的电网电压,其幅值仍为Um。
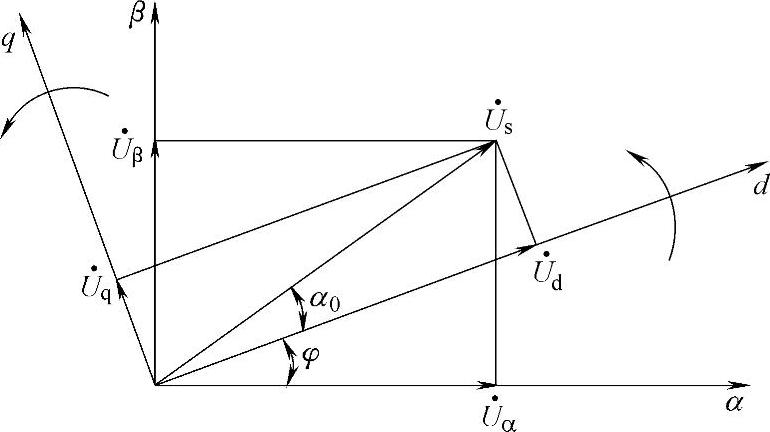
图3-106 坐标系间的关系
以上介绍了中性点钳位式三电平PWM整流器的SVPWM控制算法和采用SVPWM的中性点钳位式三电平PWM整流器的闭环矢量控制。SVPWM算法及其闭环矢量控制方法还可以推广到中性点钳位式五电平、七电平PWM整流器中。
当前,PWM整流器在工程中的应用越来越多、越来越广泛,终将成为整流技术的主流;PWM整流技术的研究与开发已全面展开;性能优良的PWM整流器将不断被推向工程应用,呈现出光明的应用前景。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




