相控整流电路带反电动势负载的工作情况分析

直流电动机负载除了具有电枢电阻、电感之外，还有一个电枢反电动势E_M，这是区别于阻感负载的一个显著特点。

图3-45是三相半波相控整流电路向电动机供电的电路图。在这样的电路中，晶闸管加触发脉冲后能否导通，取决于电动机的反电动势E_M和电感中的感应电动势e_L的代数和是否小于变压器二次绕组的瞬时电压。在整流情况下，电动机反电动势E_M的极性总是与整流电压的极性相反，容易判别。至于e_L的极性，则视电流的变化情况而定。当电流增加时，e_L的极性与整流电压极性相反，当电流减小时，e_L的极性与整流电压极性相同。当电流不变时，电感电动势为零。

如果电动机的电枢电感较小可以忽略，认为L=0，则电压和电流波形如图3-46所示。当α＜α₁时，u_a＜E_M，晶闸管承受反压不能触发导通。

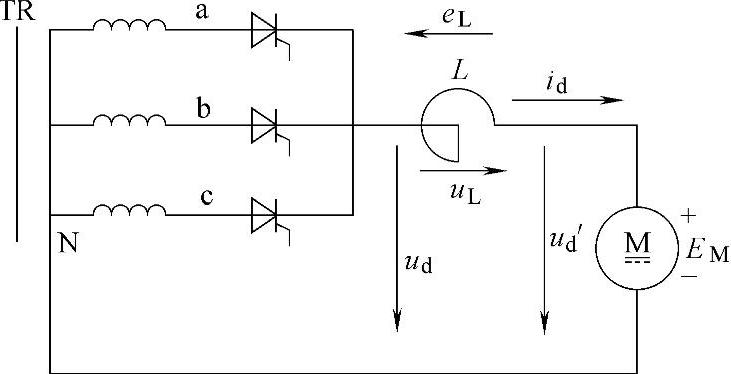
图3-45 串联电感的反电动势负载电路图

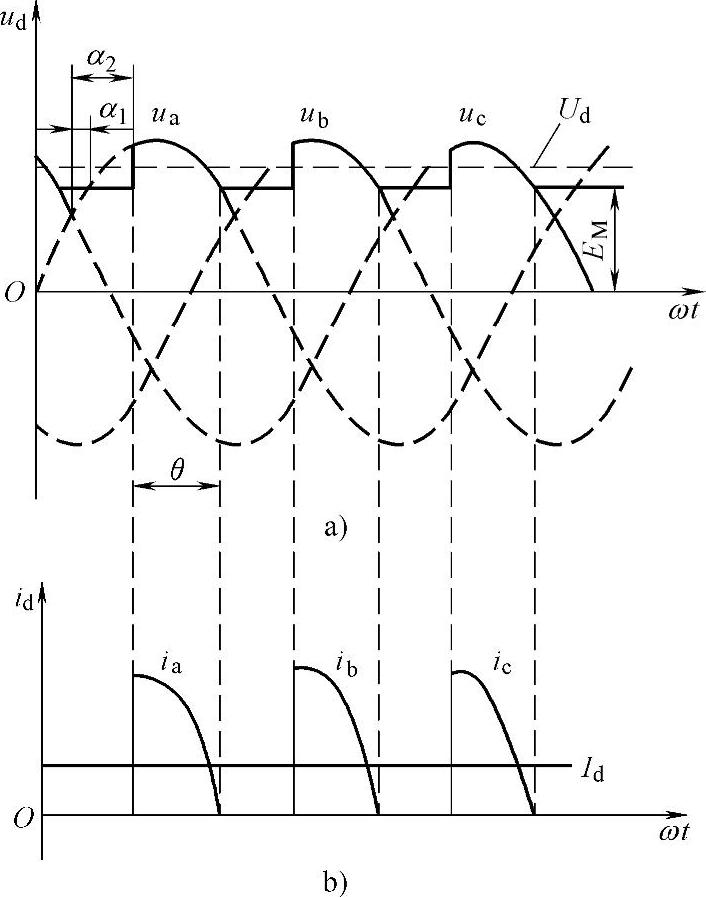
图3-46 L=0时的整流波形

当α≥α₁（如α=α₂）时，u_a＞E_M，VT₁受正压得到触发而导通。由于电路中没有电感（电枢电感已忽略），故晶闸管导通后负载电流按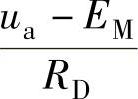突然升高。因电动机有机械惯性，转速n来不及改变，即反电动势E_M不变，故i_d随u_a变化而变化。当u_a过了最大值后重新与E_M相等时，电流降到零，晶闸管关断，整流电压、电流波形如图3-46所示。从图中可以看出，晶闸管VT₁仅在u_a＞E_M的很小一段时间里导通。VT₁导通时负载两端电压为u_a；而在其余时间里，负载两端电压皆为E_M。这样在相同触发延迟角下，整流电压平均值比电阻负载、电感负载时都高。特别是晶闸管导通角θ减小，会带来以下一系列问题：

1）若输出和电阻负载同样大小的电流（平均值），通过晶闸管的电流峰值很高，因而其有效值比电阻负载时要大许多，使晶闸管利用率降低。

2）由于电流脉动大，会使电动机换向恶化，并且增加电动机损耗，温升增高。

3）由于电流峰值增高，即要求（u₂-E_M）差值大。所以当负载增大时，则E_M必须下降很多，才能产生一定大小的I_d，即电动机转速n也必须下降很多，这就是说当负载变化时，电动机的机械特性变得很软。

为了克服上述缺点，要在整流电路中串入滤波电抗器。有了电抗器的滤波作用，整流电路的工作情况就接近于电感负载了。

由于有了电感，当晶闸管供电给直流电动机时，每一瞬间电流的变化率决定于外加电压u₂、电动机反电动势E_M、回路中电阻压降和电感产生的感应电动势e_L的数值。电压平衡方程为

(www.xing528.com)

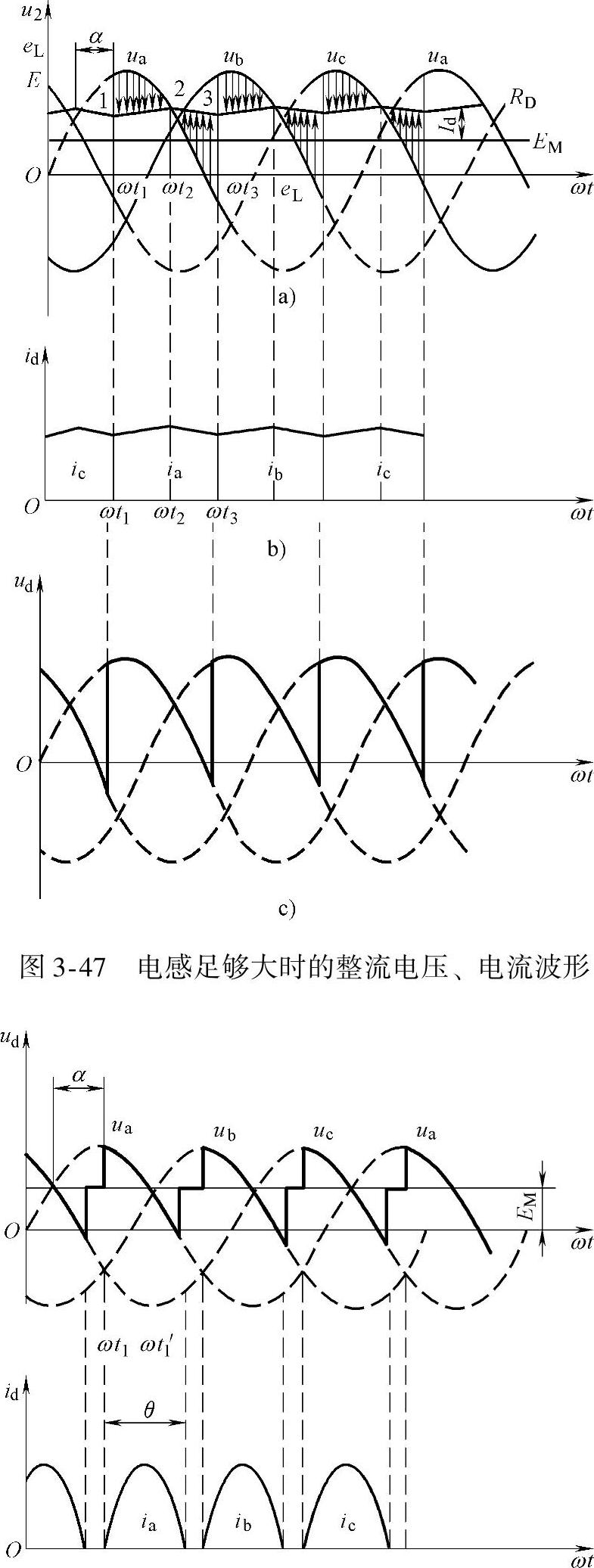
图3-48 电流断续时整流电压、电流波形

图3-47是这种情况下的整流电压、电流波形，图3-47a中曲线1-2-3与u₂的距离代表电感中感应电动势的大小，此曲线与E_M的距离表示i_dR_D的大小。

在ωt₁时触发VT₁，因u_a＞E_M，VT₁导通且电流i_d增加，L中感应电动势阻碍电流增加，此时电压平衡方程式为

u_a=E_M+i_dR_D+e_L （3-116）

在ωt₁～ωt₂期间，随着u₂与E_M间差值的减少，i_d上升越来越慢，到2点时i_d增加到最大值di_d/dt=0，故e_L=0，此时

u_a=E_M+i_dR_D （3-117）

过了ωt₂以后，在ωt₂～ωt₃期间，u_a＜E_M+i_dR_D，电流i_d减小，于是e_L改变方向，此时

u_a=E_M+i_dR_D-e_L （3-118）

由于e_L的数值较大，因此即使u_a变为负值时，因e_L-E_M＞u_a，VT₁仍受正向电压而继续导通。在ωt₃时，触发VT₂导通，VT₁受反压关断。以后又重复上述过程。

由上面分析可知，当平波电感L足够大时，整流电流连续，整流电压u_d波形与大电感负载时相同，完全决定于相电压u_a（或u_b、u_c）及触发延迟角α，而与反电动势大小无关。这时整流电压所包含的交变分量大部分降落在电抗器上，电动机两端电压基本保持恒定不变，等于反电动势与电枢电阻压降之和。相应负载电流也与电感负载相同，是连续平滑的。

整流电路虽有电感，但当负载电流较小时，电感储能少，不足以维持电流连续，图3-48所示为这种情况下三相半波整流电路向电动机供电时的波形。在ωt₁时，VT₁触发导通，整流电压u_d=u_a，由于电感L的作用，在u_a＜E_M后，VT₁继续导通，直到ωt′₁时，由于e_L＜E_M+u_a，故VT₁受反向电压而关断，电流i_d=0，e_L=0，这时整流输出电压又变为E_M。

由上面分析可知，相控整流电路给直流电动机电枢供电时，电路中虽串有电抗器，但当电流较小时（转速接近空载转速时），电流仍会出现断续现象，这就使电动机在小负载时电压显著升高，而当负载变大时，电流重新连续，电压又下降很多，故电压调整率差，电动机的机械特性因电流断续而变差。这是晶闸管电动机系统存在的特殊问题，这个问题会对晶闸管电动机系统的机械特性产生影响，将在后续课程中讲述。