相控整流电路谐波及功率因数优化分析

电力电子装置的使用会带来谐波和功率因数问题。谐波的产生会引起电网谐波污染和控制系统的误动作，对通信系统产生干扰，使电气传动系统产生振动、噪声等不良后果。而功率因数的下降会产生电网无功电流增加、电压波动等不利影响。因此有必要对谐波和功率因数问题进行分析，找出相应的改善方法。

1.相控整流电路的谐波及功率因数概念

（1）谐波

在电力电子电路的分析中经常会遇到非正弦电压、电流波形，这主要是由非线性负载引起的。当正弦电压加到非线性负载上时，会产生非正弦电流，而非正弦电流又会在负载上产生压降，使电压波形也成为非正弦波。

非正弦的电压u（ωt）和非正弦的电流i（ωt）可分解成傅里叶级数为

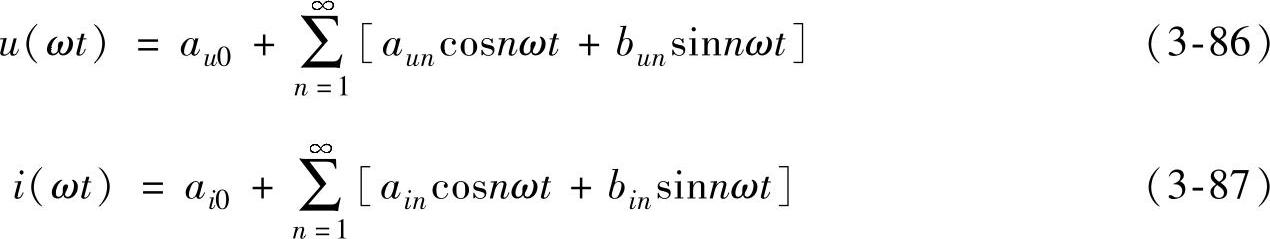
式中

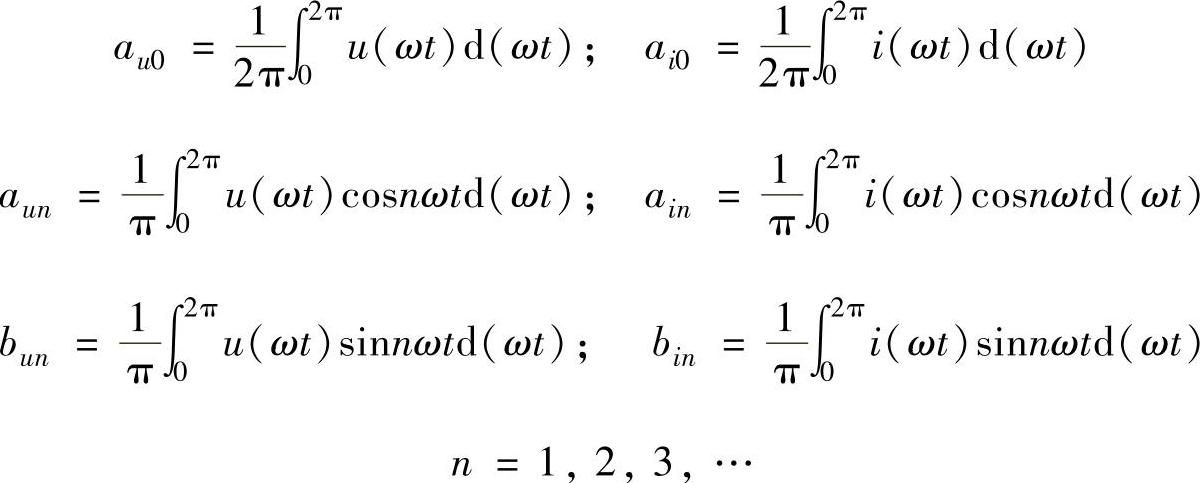
在上述电压、电流的傅里叶级数表达式中，频率与工频相同的分量称为基波，而频率为基波频率整数倍的分量称为谐波，谐波次数为谐波频率和基波频率的整数比（大于1）。

（2）功率因数

晶闸管变流装置的功率因数是指装置交流侧有功功率与视在功率之比。变流装置的功率因数与电压、电流间的滞后角，交流侧（电网侧）的感抗和电流波形有关。

相控整流电路由于实行触发时刻或相位的控制，造成电压、电流波形非正弦，因此电路的功率及功率因数的计算须按非正弦电路的方法进行。电压、电流的有效值应为各次谐波有效值的均方根值，即

式中，U_d、I_d为电压、电流的直接平均值，U_dk、I_dk为各次谐波电压、电流有效值。

电路的视在功率、有功功率和无功功率分别为

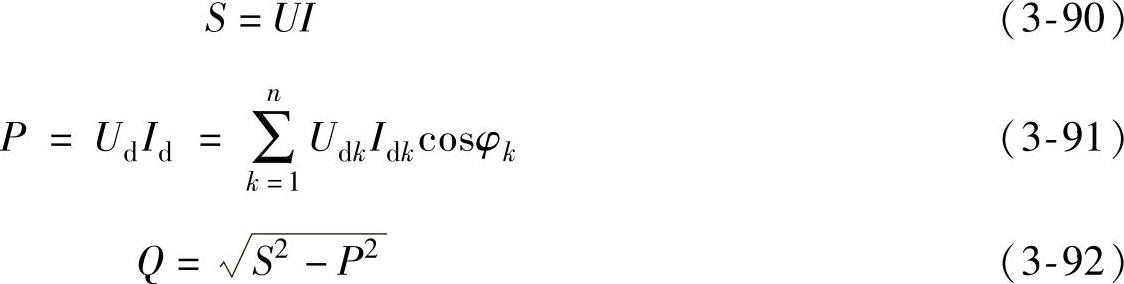
式中，φ_k为k次谐波电压、电流间的相位差。

由于电网电压波形的畸变不大，在实际计算时，可将电压近似为正弦波，只考虑电流为非正弦波。设正弦波电压有效值为U，畸变电流有效值为I，基波电流有效值为I₁，基波电流有效值与电压的相位差为φ₁，这时有功功率为

P=UI₁cosφ₁ （3-93）

功率因数为

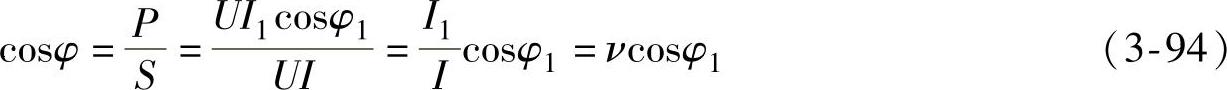
式中，ν=I₁/I，即基波电流有效值和总电流有效值之比，称为基波因数，而cosφ₁称为位移因数或基波功率因数。可见，功率因数由基波电流相位移和电流波形畸变这两个因素共同决定。

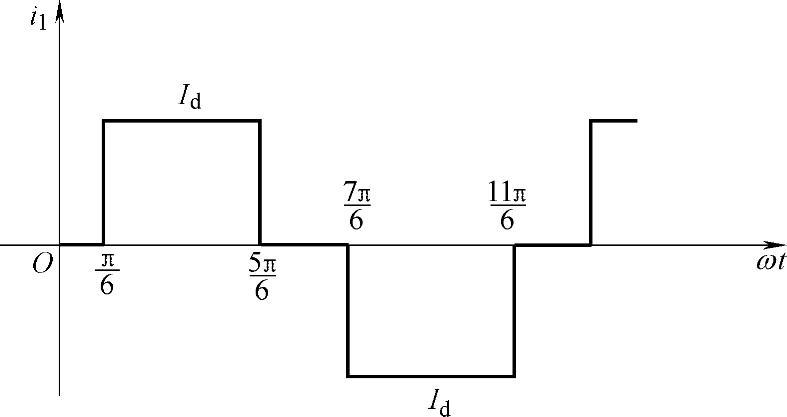
图3-42 三相全控桥式相控整流电路交流侧电流波形

2.交流输入侧的谐波分析

以三相全控桥式相式整流电路为例，为了简化分析，设三相全控桥式相控整流电路中整流变压器的一、二次绕组都是星形联结，交流侧电抗为零，直流侧电感L为足够大，即忽略换相过程和电流脉动情况，交流侧电流波形如图3-42所示。

在任何触发延迟角α情况下，每个晶闸管的导通角始终是120°，流过整流变压器二次侧的每相电流i₁为正负半周各120°的矩形波。三相电流波形相同，且依次相差120°。对于这个波形，可以根据傅里叶级数进行分解。

因f（ωt）=-f（ωt+π），故不会有偶次项谐波，将方波电流分解为傅里叶级数可得

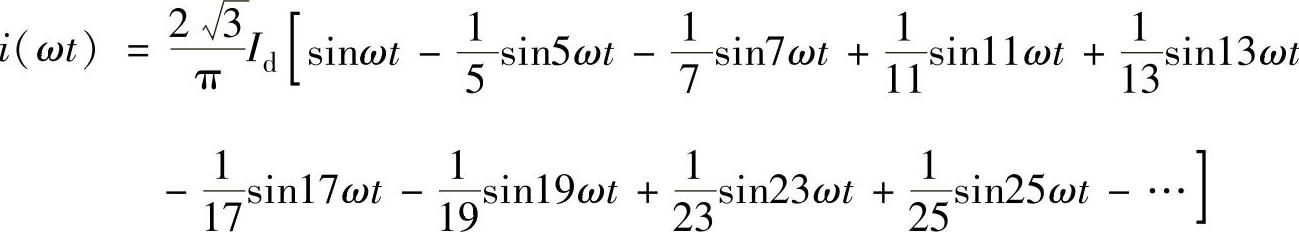
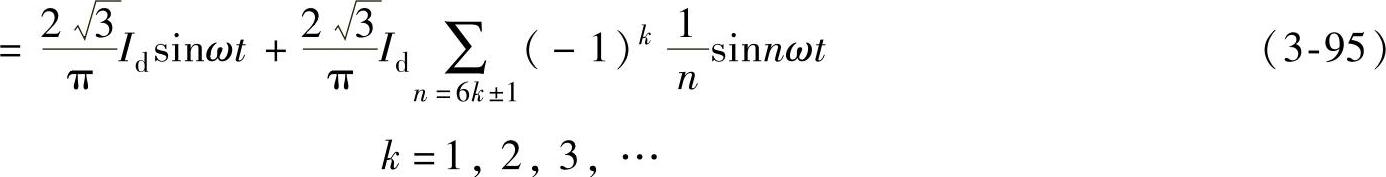
可以看出，方波电流中含有大量的5、7、11、13等次谐波，这些谐波电流在电网回路会引起阻抗压降，因而使电网电压也含有谐波成分，造成电网电压畸变。因此晶闸管装置实际上可以看成是一个谐波源。

3.相控整流器交流输入侧的功率因数

三相桥式全控相控整流电路中，可由式（3-95）得出电流基波和各次谐波的有效值分别为

交流侧电流有效值与直流电流的关系为

由式（3-96）和式（3-97）可得电流基波因数为

由于电流基波与电压的相位差仍为α，故位移因数仍为

cosφ₁=cosα （3-99）

功率因数即为

cosφ=νcosφ₁≈0.955cosα （3-100）

由式（3-100）可以看出，交流装置在整流工作状态下，功率因数与装置所带负载性质无关，主要决定于触发延迟角α的余弦。随着α的增大，功率因数下降。这是由于α越大，电压、电流波形间的相位差也越大。负载电流一定时，输入视在功率近似不变，输出有功功率则随整流电压的降低而减小。

4.相控整流器输出侧的谐波分析

相控整流电路输出的脉动直流电压都是周期性的非正弦函数，若用傅里叶级数表示整流电路输出的脉动直流电压，可分为直流电压U_d及各次谐波电压u_n，其谐波对于负载的工作是不利的。

（1）α=0°时m相整流电路分析

以α=0°时，m相脉波相控整流电路（设m=

3）为例，其输出直流电压波形如图3-43所示。

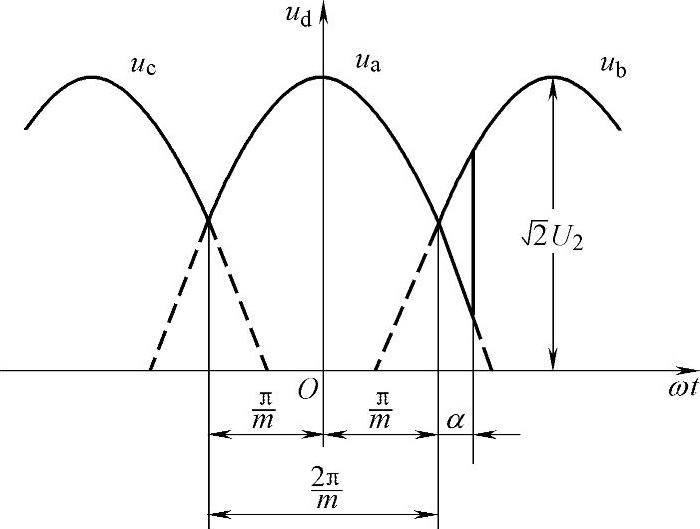
图3-43 m相脉波相控整流电路输出电压波形(www.xing528.com)

在一个周期内，输出电压有m个形状相同、相位相差2π/m的电压脉波，将纵轴坐标选在整流电压的峰值处，则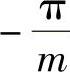到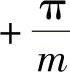区间，整流电压的表达式为

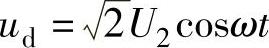
根据傅里叶级数分析，全部整流电压可分解为

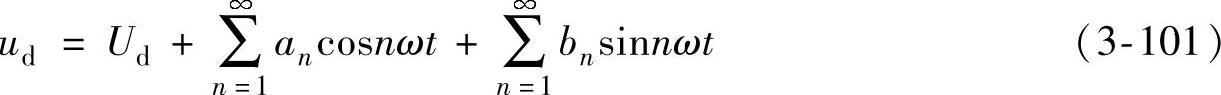
由于电压波形关于y轴对称，即u_d（ωt）=u_d（-ωt），故只有余弦函数才符合要求，正弦函数不再存在。因此式（3-101）可简化为

又因u_d以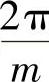为周期重复出现，则应有

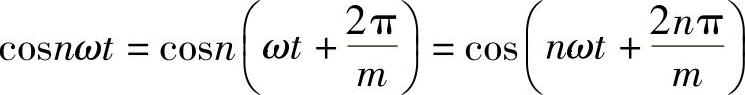
这种情况只有当

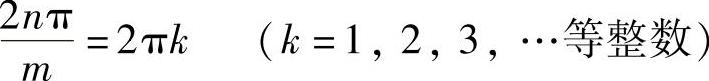
时方有可能成立，所以

n=mk

即在余弦项中，n一定是m的整数倍，如m为三相，则n=3，6，9等，只有3的倍数次谐波出现，其他谐波均不存在。

整流电压平均值U_d为

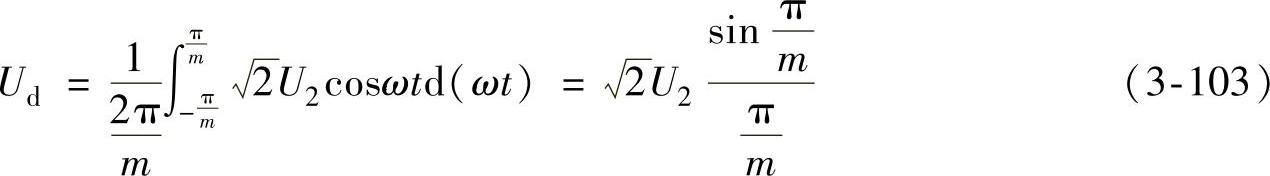
根据傅里叶级数分析可求得

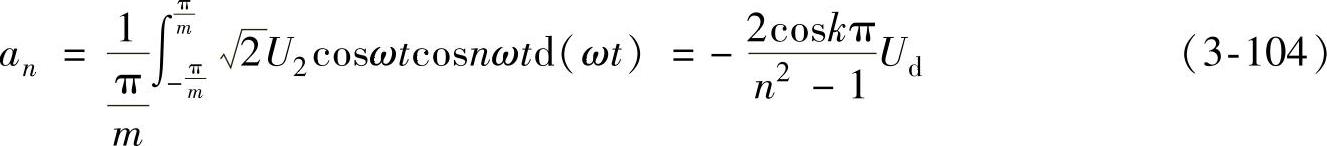
将式（3-103）和式（3-104）代入式（3-102），得

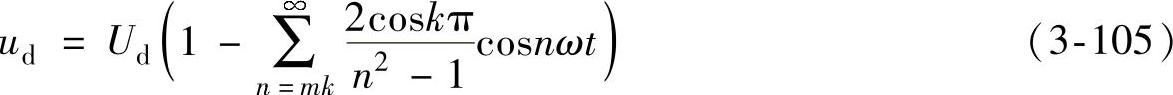
三相半波相控整流电路时，m=3，代入式（3-104）和式（3-105），得

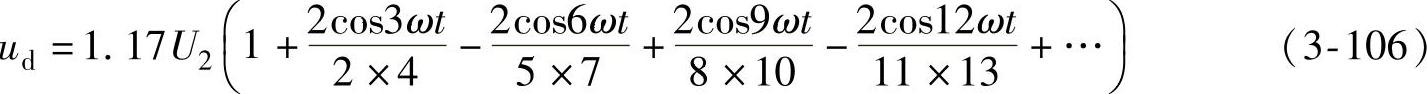
三相全控桥式相控整流电路时，m=6，输出电压为线电压，将U_2L替换U₂代入式（3-104），然后代入式（3-105），得

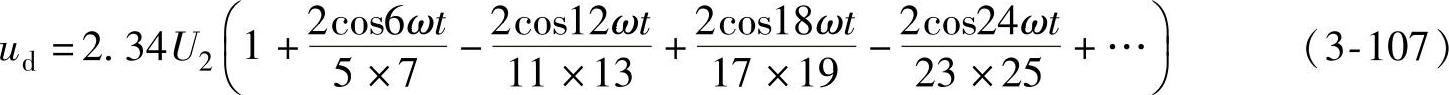
由以上结果可知，相数m的增加使最低次谐波的频率增加，同时，其幅值也迅速减小，这个结论对于大功率整流电路的结构选择，有很重要的意义。

为了描述整流电压u_d所含谐波的总体情况，定义电压纹波因数γ_u为u_d中谐波分量有效值U_R与整流电压平均值U_d值之比，即

其中

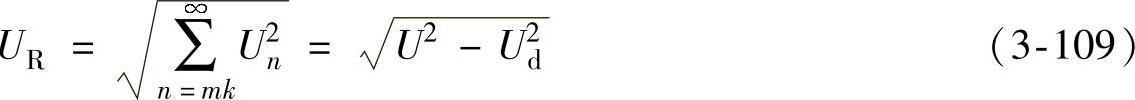
式中整流电压有效值U为

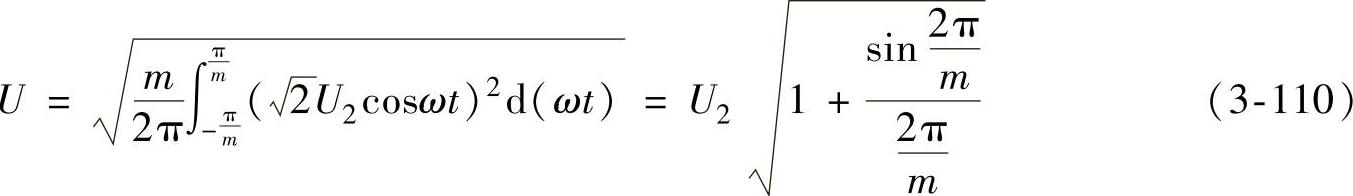
将式（3-109）、式（3-110）和式（3-103）代入式（3-108）得

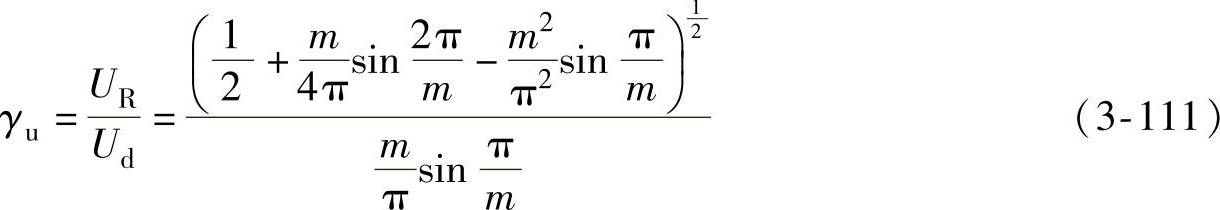
表3-2为不同相数时的纹波因数值。

表3-2 不同相数时的纹波因数值

从表中可以看出，当m=6时，纹波因数已很小，它只有6次、12次、18次、…谐波电压。因此相数越多，输出直流电压的交流分量就越小。

（2）α＞0°时三相桥式相控整流电路谐波分析

当α＞0°时，随着不同的负载情况，整流电压的波形分析分为断续与连续两种情况。用上述分析方法，不能简单地得出一般多相整流的谐波分析。工业上最常用的是三相全控桥式相控整流电路，下面集中分析三相全控桥式相控整流电路电流连续时的谐波幅值问题。

负载电压的傅里叶级数表达式为

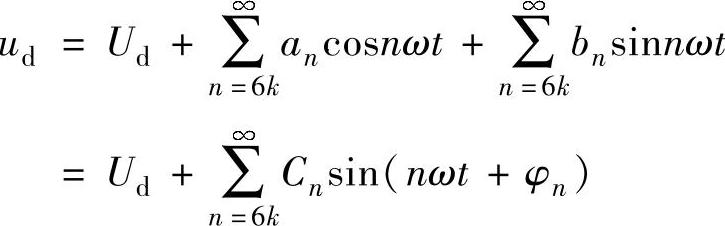
以三相线电压u_ab的零点作为坐标原点，有

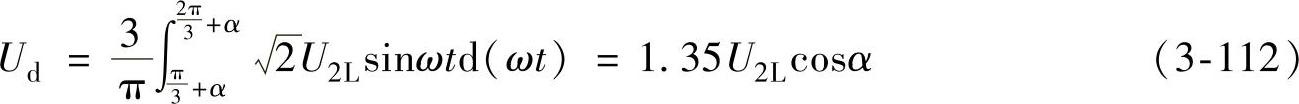
下列关系仍保持成立，即

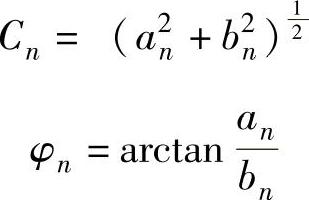
由于u_d的基频是6ω，可用下面的积分形式确定a_n和b_n，即

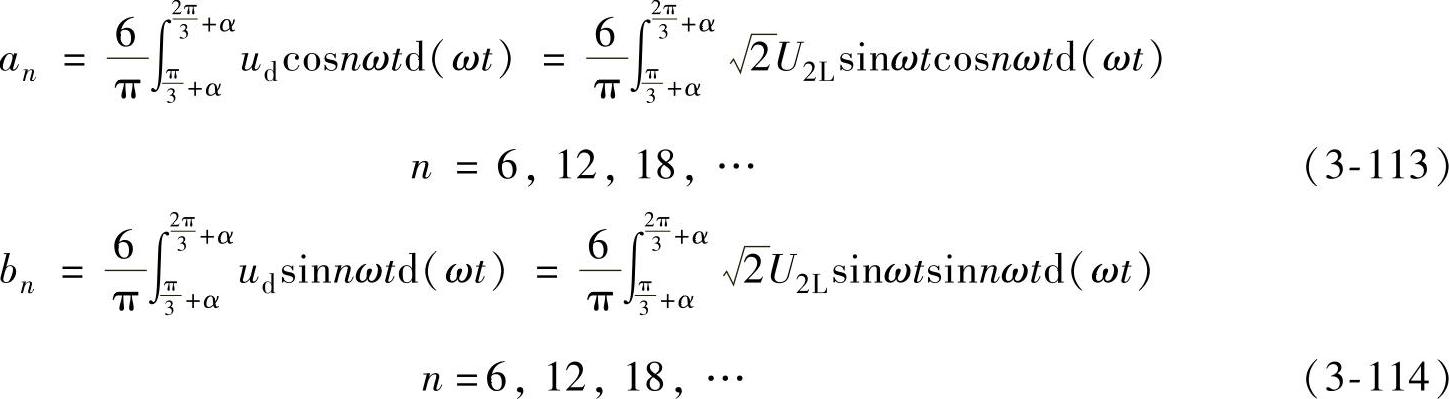
以n为参变量的谐波幅值的标幺值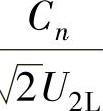与α的关系如图3-44所示。由图可见，α=90°时，谐波幅值最大。

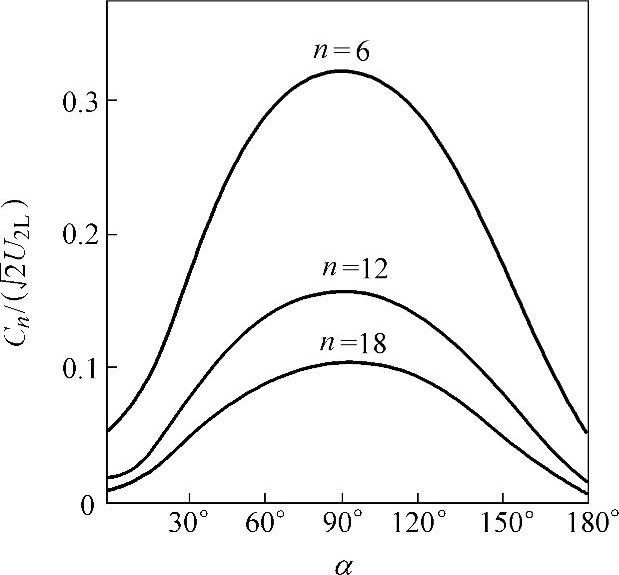
图3-44 三相全控桥式相控整流电路电流连续情况下，以n为参变量的C_n/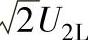（）与α的关系