单相不控整流电路的电容滤波方案

电容滤波的单相不控整流电路常用于小功率单相交流输入的场合。目前大量普及的微机、电视机等电气产品所采用的开关电源中，其整流部分就是如图3-2a所示的单相桥式不控整流电路。以下就对该电路的工作原理进行分析，总结其特点。

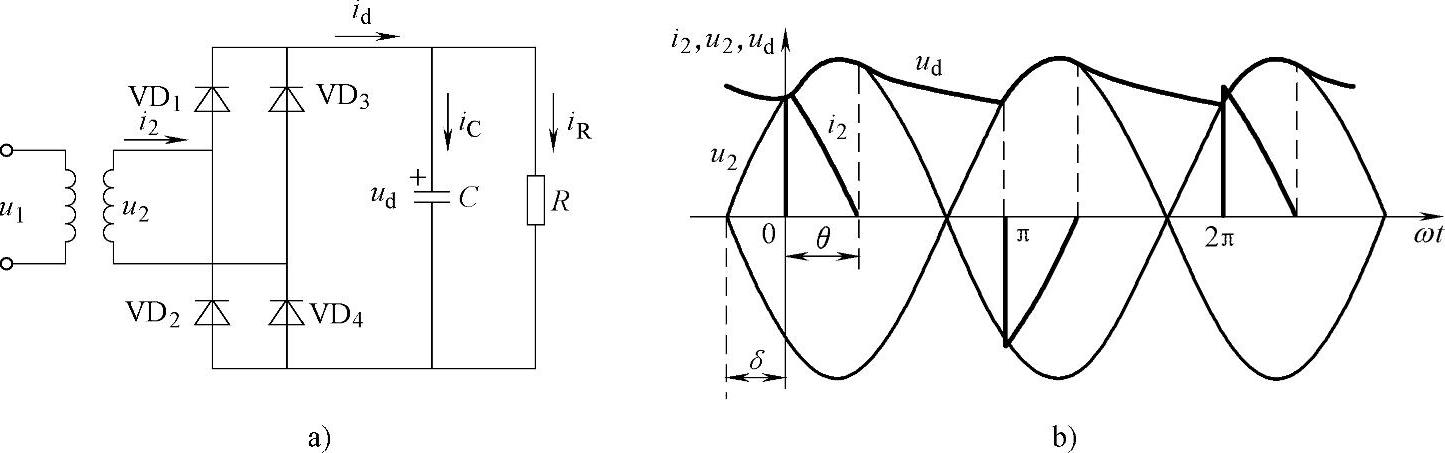
图3-2 电容滤波的单相桥式不控整流电路及其工作波形

a）电路 b）波形

1.工作原理及波形分析

图3-2b为电路工作波形。假设该电路已工作于稳态，并以电阻R作为负载。工作原理及波形分析如下：

电路的基本工作过程是，在u₂正半周过零点至ωt=0期间，因u₂＜u_d，故二极管均不导通，此阶段电容C向R放电，提供负载所需电流，同时u_d下降。至ωt=0之后，u₂将要超过u_d，使得VD₁和VD₄开通，u_d=u₂，交流电源向电容充电，同时向负载R供电。

设VD₁和VD₄导通的时刻与u₂过零点相距δ角，则u₂为

在VD₁和VD₄导通期间，有

式中，u_d（0）为VD₁、VD₄开始导通时刻直流侧电压值。

将u₂代入并求解得

而负载电流为

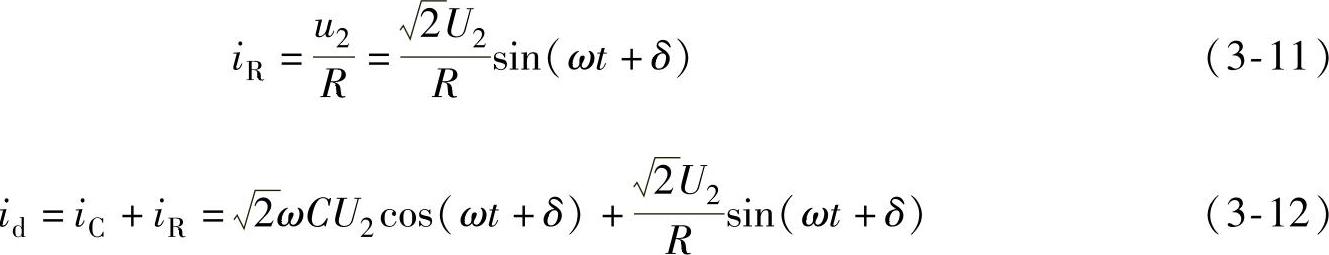
设VD₁和VD₄的导通角为θ，则当ωt=θ时，VD₁和VD₄关断。将i_d（θ）=0代入式（3-12）得

tan（θ+δ）=-ωRC （3-13）

电容被充电到ωt=θ时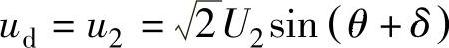，，VD₁和VD₄关断。电容开始以时间常数RC按指数函数放电，当ωt=π，即放电经过π-θ角时，u_d降至开始充电时的初值2U₂sinδ，另一对二极管VD₂和VD₃导通，此后u₂又向C充电，与u₂正半周的情况一样。由于二极管导通后u₂开始向C充电时的u_d与二极管关断后C放电结束时的u_d相等，故有

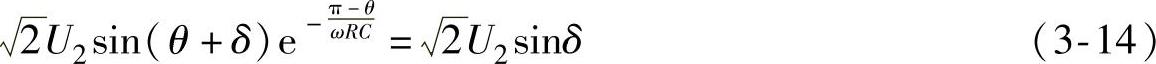
注意到θ+δ为第2象限的角，由式（3-13）和式（3-14）得

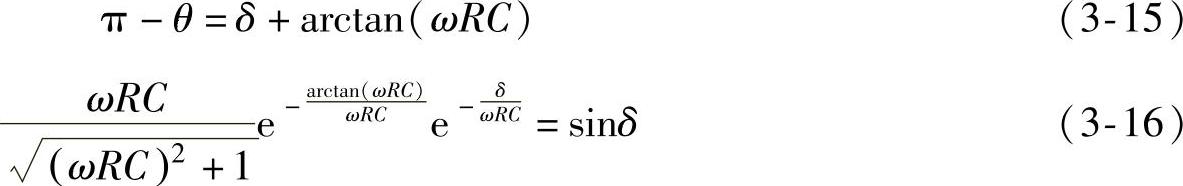
在ωRC已知时，即可由式（3-16）求出δ，进而由式（3-15）求出θ。显然δ和θ仅由ωRC决定。图3-3给出了根据以上两式求得的δ、θ随ωRC变化的曲线。

二极管VD₁和VD₄关断的时刻，即ωt达到θ的时刻，还可用另一种方法确定。显然，在u₂达到峰值之前，VD₁和VD₄是不会关断的。u₂过了峰值之后，u₂和电容电压u_d都开始下降。VD₁和VD₄的关断时刻，从物理意义上讲，就是两个电压下降速度相等的时刻，一个是电源电压的下降速度|du₂/d（ωt）|，另一个是假设二极管VD₁和VD₄关断而电容开始单独向电阻放电时电压的下降速度|du_d/d（ωt）|_p（下标表示假设）。前者等于该时刻u₂导数的绝对值，而后者等于该时刻u_d与ωRC的比值。据此即可确定θ。(www.xing528.com)

2.数量关系

（1）输出电压平均值

空载时，R=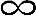，放电时间常数为无穷大，输出电压最大，。

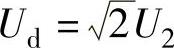整流电压平均值U_d可根据前述波形及有关计算公式推导得出，但推导过程繁琐，故此处直接给出U_d与输出到负载的电流平均值I_R之间的关系如图3-4所示。空载时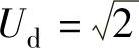，。重载时，R很小，电容放电很快，几乎失去储能作用，随着负载加重，U_d逐渐趋近于0.9U₂，即趋近于接近电阻负载时的特性。

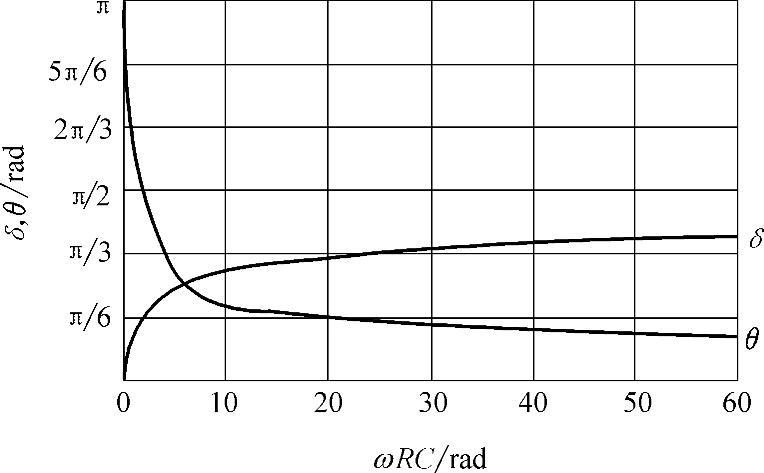
图3-3 δ、θ随ωRC变化的曲线

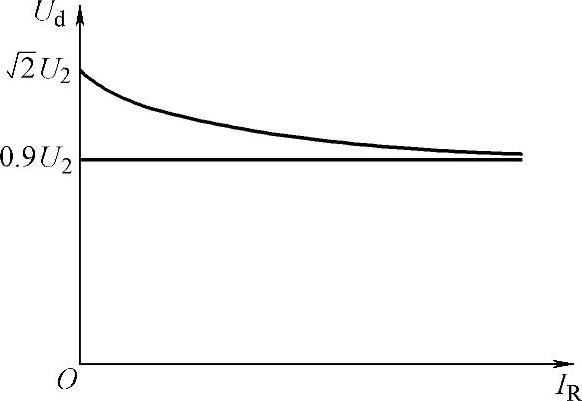
图3-4 电容滤波的单相不控整流电路输出电压与输出电流的关系

通常在设计时根据负载的情况选择电容C值，使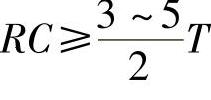，T为交流电源的周期，此时输出电压为

U_d≈1.2U₂ （3-17）

（2）电流平均值

输出电流平均值I_R为

I_R=U_d/R （3-18）

在稳态时，电容C在一个电源周期内吸收的能量和释放的能量相等，其电压平均值保持不变，相应地，流经电容的电流在一周期内的平均值为零，又由i_d=i_C+i_R得

i_d=i_R （3-19）

在一个电源周期中，i_d有两个波头，分别轮流流过VD₁、VD₄和VD₂、VD₃。反过来说，流过某个二极管的电流i_VD只是两个波头中的一个，故其平均值为

I_VD=I_d/2=I_R/2 （3-20）

（3）二极管承受的电压

二极管承受的反向电压最大值为变压器二次电压最大值，即。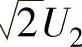

在以上讨论过程中，忽略了电路中诸如变压器漏抗、线路电感等的作用。另外，实际应用中为了抑制电流冲击，常在直流侧串入较小的电感，成为感容滤波的电路，如图3-5a所示。此时输出电压和输入电流的波形如图3-5b所示，由波形可见，u_d波形更平直，而电流i₂的上升段平缓了许多，这对于电路的工作是有利的。当L与C的取值变化时，电路的工作情况会有很大的不同，这里不再详细介绍。

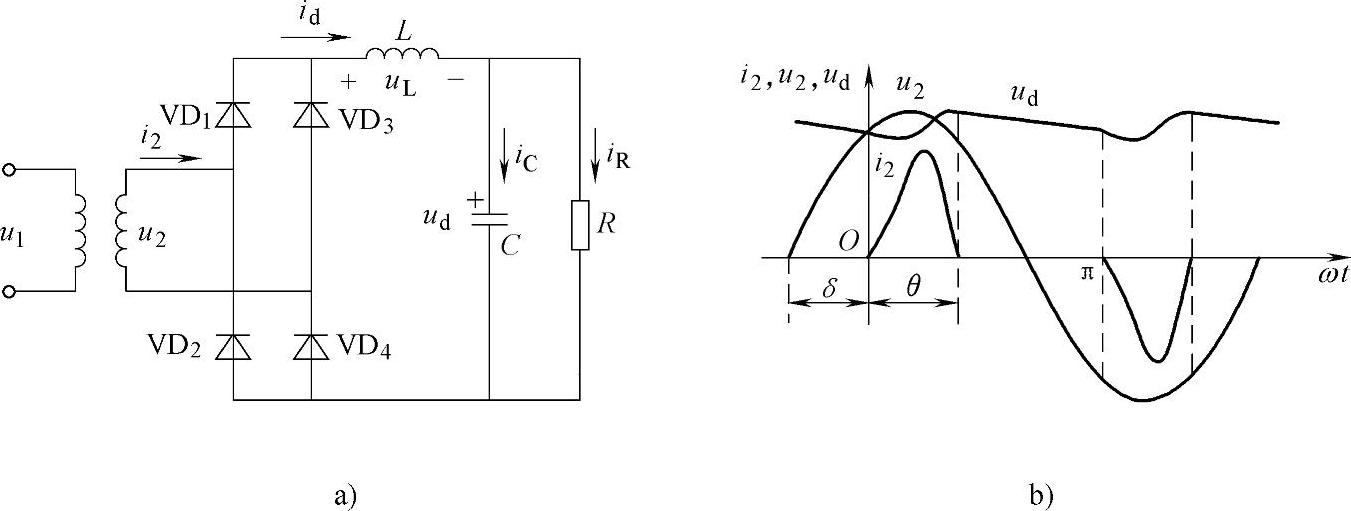
图3-5 感容滤波的单相桥式不控整流电路及其工作波形

a）电路图 b）波形