电压空间矢量PWM控制技术——SVPWM逆变器优化方案

SVPWM控制技术在用于交流电机驱动的各种变频器中使用最多。SPWM技术是从电源的角度出发的，目的在于生成一个可以调频调压的三相对称正弦波供电电源，控制原则是尽可能降低输出电压的谐波分量，使其逼近正弦波形。与这种SPWM技术不同，电压空间矢量PWM技术则是从电动机的角度出发的，目的在于使交流电动机产生圆形磁场。它是以三相对称正弦波电源（其电压和频率值均为电动机的额定值）供电时交流电动机产生的理想磁链圆为基准，通过选择逆变器的不同开关模式，电动机的实际磁链尽可能逼近理想磁链圆。这种以圆形旋转磁场为目标来控制逆变器工作的控制方法称为磁链跟踪控制，磁链轨迹的控制是通过交替使用不同的电压空间矢量来实现的，所以又称电压空间矢量PWM控制。

由于SVPWM逆变器具有开关损耗低、便于微机实时控制、电压利用率高等优点，所以SVPWM逆变器不仅在电动机调速系统中得到了广泛应用，而且还扩展到其他非电动机负载，例如UPS、PWM整流电路、中性点钳位式逆变器等，这些场合下，电压空间矢量仅有数学上的意义。

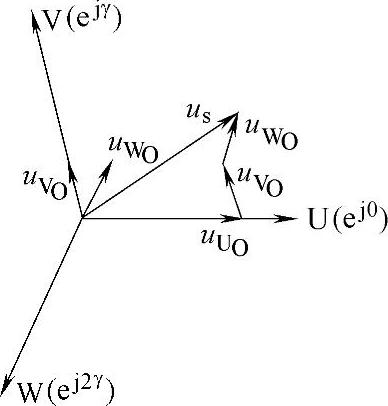
图2-37 电压空间矢量

1.电压空间矢量的定义

交流电动机绕组的电压、电流、磁链等物理量都是随时间变化的，如果考虑到它们所在绕组的空间位置，可以定义为空间矢量。在图2-37中，U、V、W分别表示在空间静止的电动机定子三相绕组的轴线，它们在空间互差2π/3，三相定子相电压u_UO、u_VO、u_WO分别加在三相绕组上。可以定义三个定子电压空间矢量u_UO、u_VO、u_WO，如图2-37所示。当u_UO＞0时，u_UO与U轴同向，u_UO＜0时，u_UO与U轴反向，V、W两相也同样如此。

其中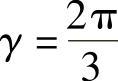，，k为待定系数。

三相合成矢量为

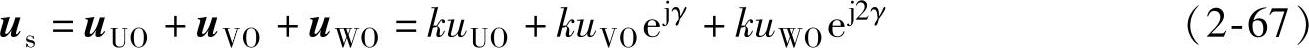
图2-37为某一时刻u_UO＞0，u_VO＞0，u_WO＜0时的合成矢量。

与定子电压空间矢量相仿，可以定义定子电流和磁链的空间矢量i_s和ψ_s分别为

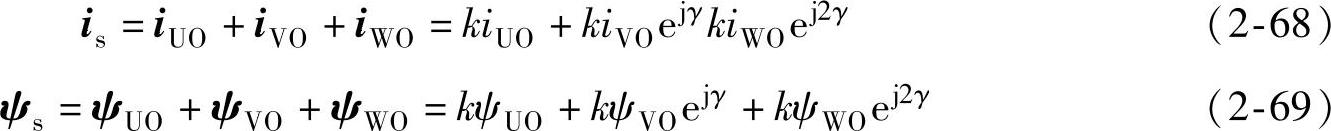
由式（2-68）和式（2-69）可得空间矢量功率的表达式为

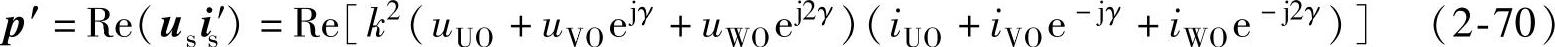
i_s′和i_s是一对共轭矢量，将式（2-70）展开，得

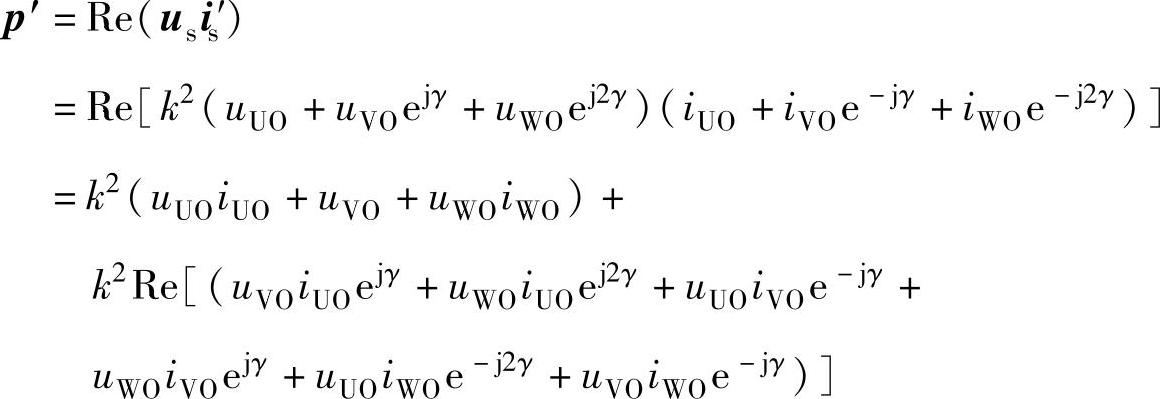
考虑到i_UO+i_VO+i_WO=0、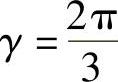，得

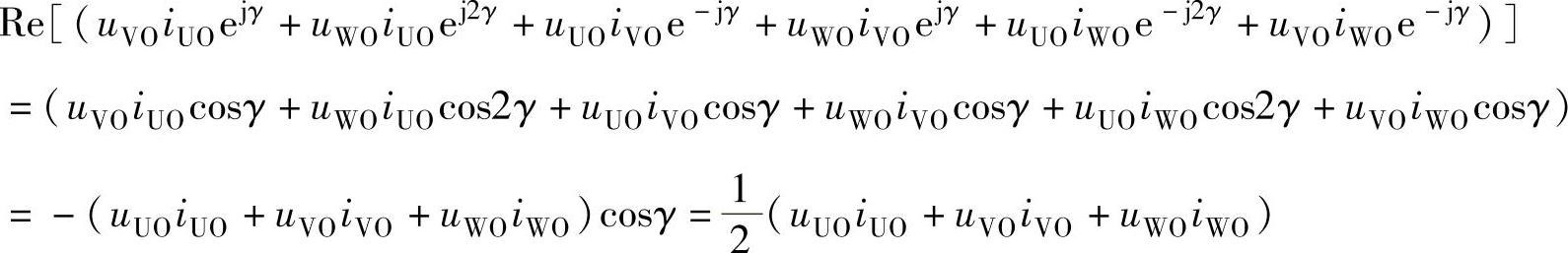
由此可得

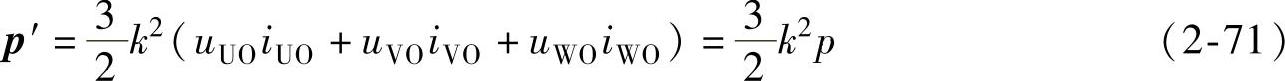
式中，p为三相瞬时功率，p=u_UOi_UO+u_VOi_VO+u_WOi_WO。

按空间矢量功率p′与三相瞬时功率p相等的原则，应使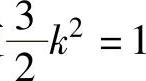，即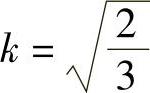。空间矢量表达式为

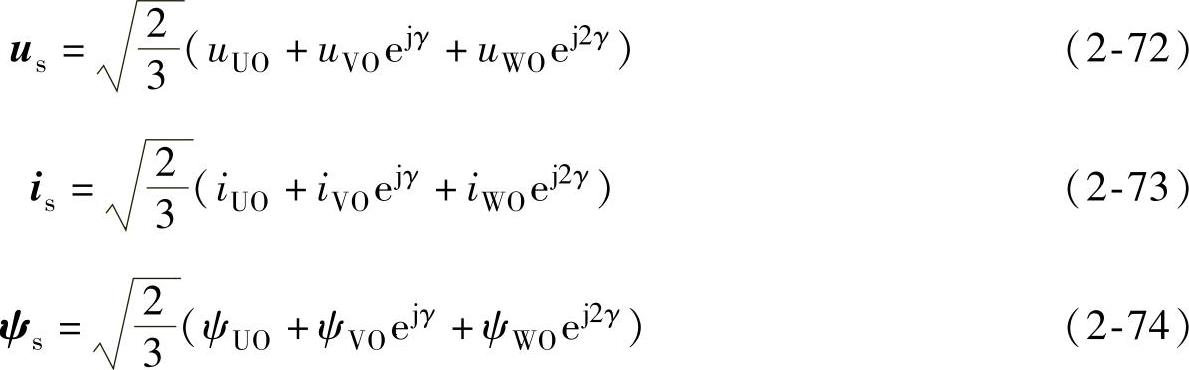
当定子相电压u_UO、u_VO、u_WO为三相平衡正弦电压时，三相合成矢量为

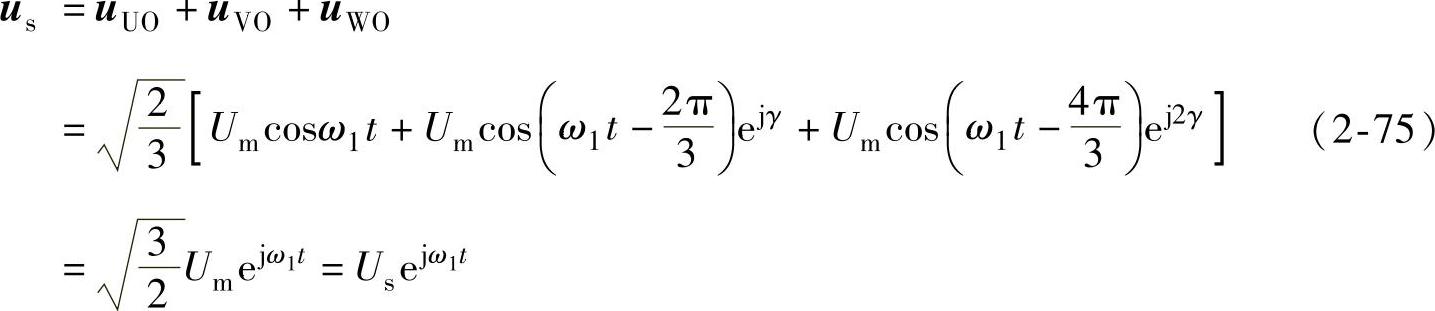
u_s是一个以电源角频率ω₁为角速度作恒速旋转的空间矢量，它的幅值是相电压幅值的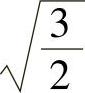倍，当某一相电压为最大值时，合成电压矢量u_s就落在该相的轴线上。在三相平衡正弦电压供电时，若电动机转速已稳定，则定子电流和磁链的空间矢量i_s和ψ_s的幅值恒定，以电源角频率ω₁为电气角速度在空间作恒速旋转。

2.电压与磁链空间矢量的关系

当异步电动机的三相对称定子绕组由三相电压供电时，对每一相都可写出一个电压平衡方程式，求三相电压平衡方程式的矢量和，即得用合成空间矢量表示的定子电压方程式为

当电动机转速不是很低时，定子电阻降压所占的成分很小，可忽略不计，则定子合成电压与合成磁链空间矢量的近似关系为

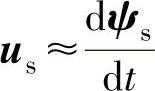
或

当电动机由三相平衡正弦电压供电时，电动机定子磁链幅值恒定，其空间矢量以恒速旋转，磁链矢量顶端的运动轨迹呈圆形（简称为磁链圆）。定子磁链旋转矢量为

式中，ψ_s表示定子磁链矢量幅值；φ表示定子磁链矢量的空间角度。

将式（2-78）对t求导得

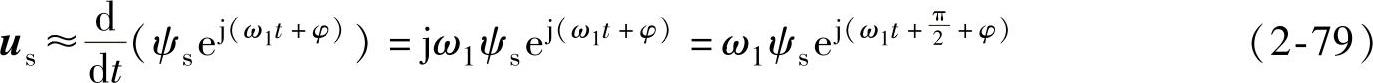
式（2-79）表明，磁链幅值ψ_s等于电压与频率之比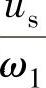，us的方向与磁链矢量ψ_s正交，即为磁链圆的切线方向，如图2-38所示。当磁链矢量在空间旋转一周时，电压矢量也连续地按磁链圆的切线方向运动2π弧度，若将电压矢量的参考点放在一起，则电压矢量的轨迹也是一个圆，如图2-39所示。因此，电动机旋转磁场的轨迹问题就可转化为电压空间矢量的运动轨迹问题。

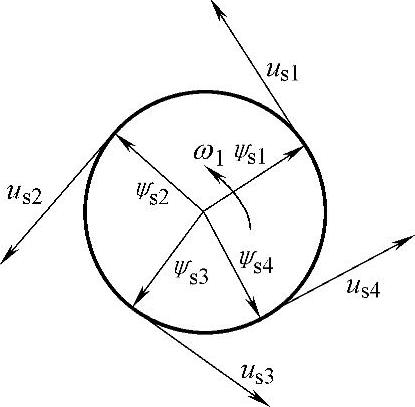
图2-38 旋转磁场与电压空间矢量的运动轨迹

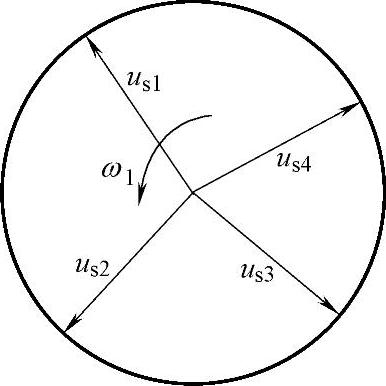
图2-39 电压矢量圆轨迹

3.PWM逆变器基本输出电压矢量

由式（2-72）得

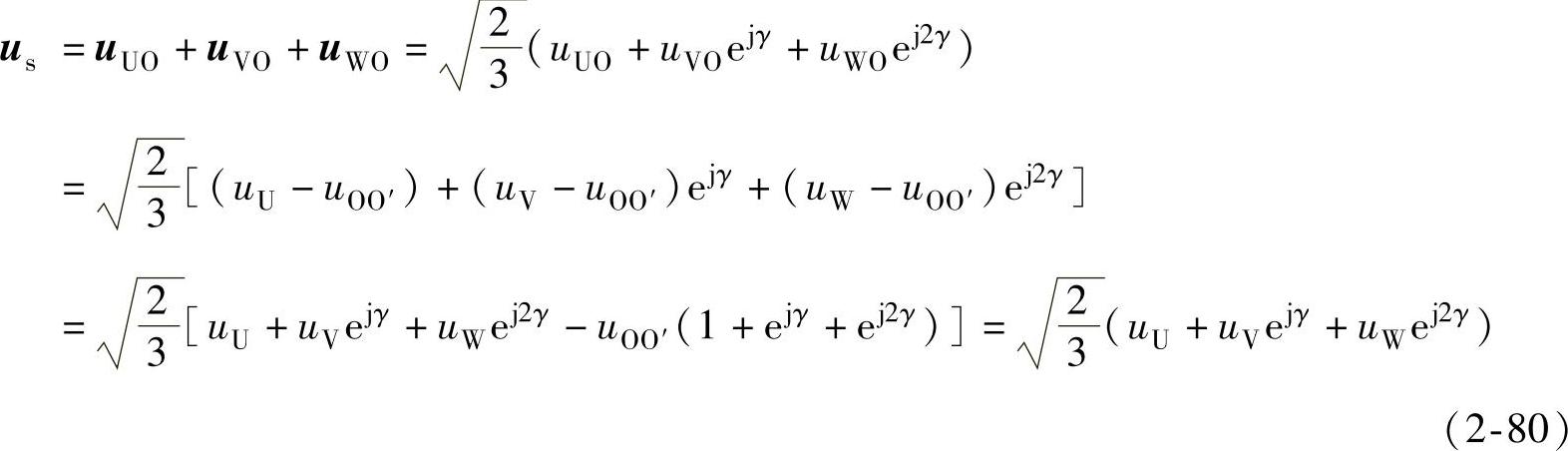
其中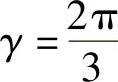，，1+e^jγ+e^j2γ=0，u_U、u_V、u_W是以直流电源中性点O′为参考点的PWM逆变器三相输出电压。由式（2-80）可知，虽然直流电源中性点O′和交流电动机中性点O的电位不等，但合成电压矢量的表达式相等。因此，三相合成电压空间矢量与参考点无关。

图2-18a所示的PWM逆变器共有八种工作状态，当（S_U，S_V，S_W）=（1，0，0）时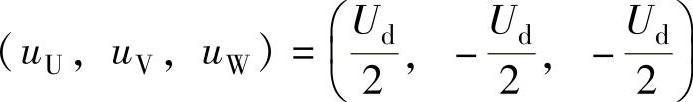，，代入式（2-80）得

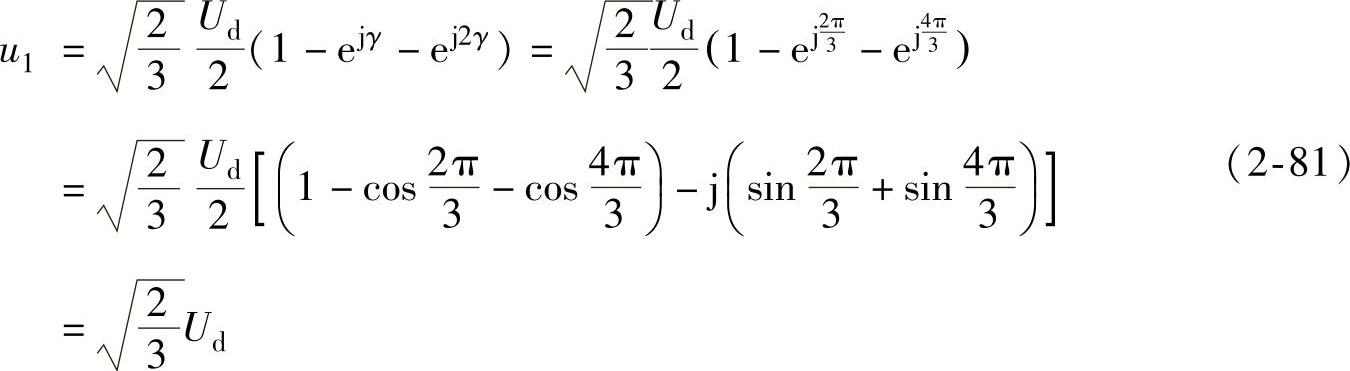
同理，当（S_U，S_V，S_W）=（1，1，0）时，（u_U，u_V，u_W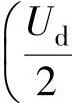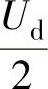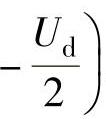）=，，，得

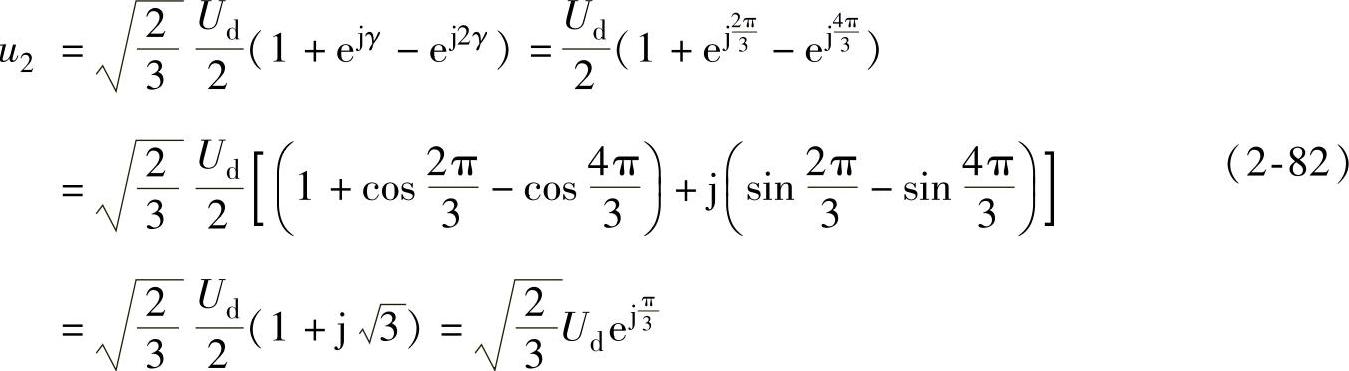
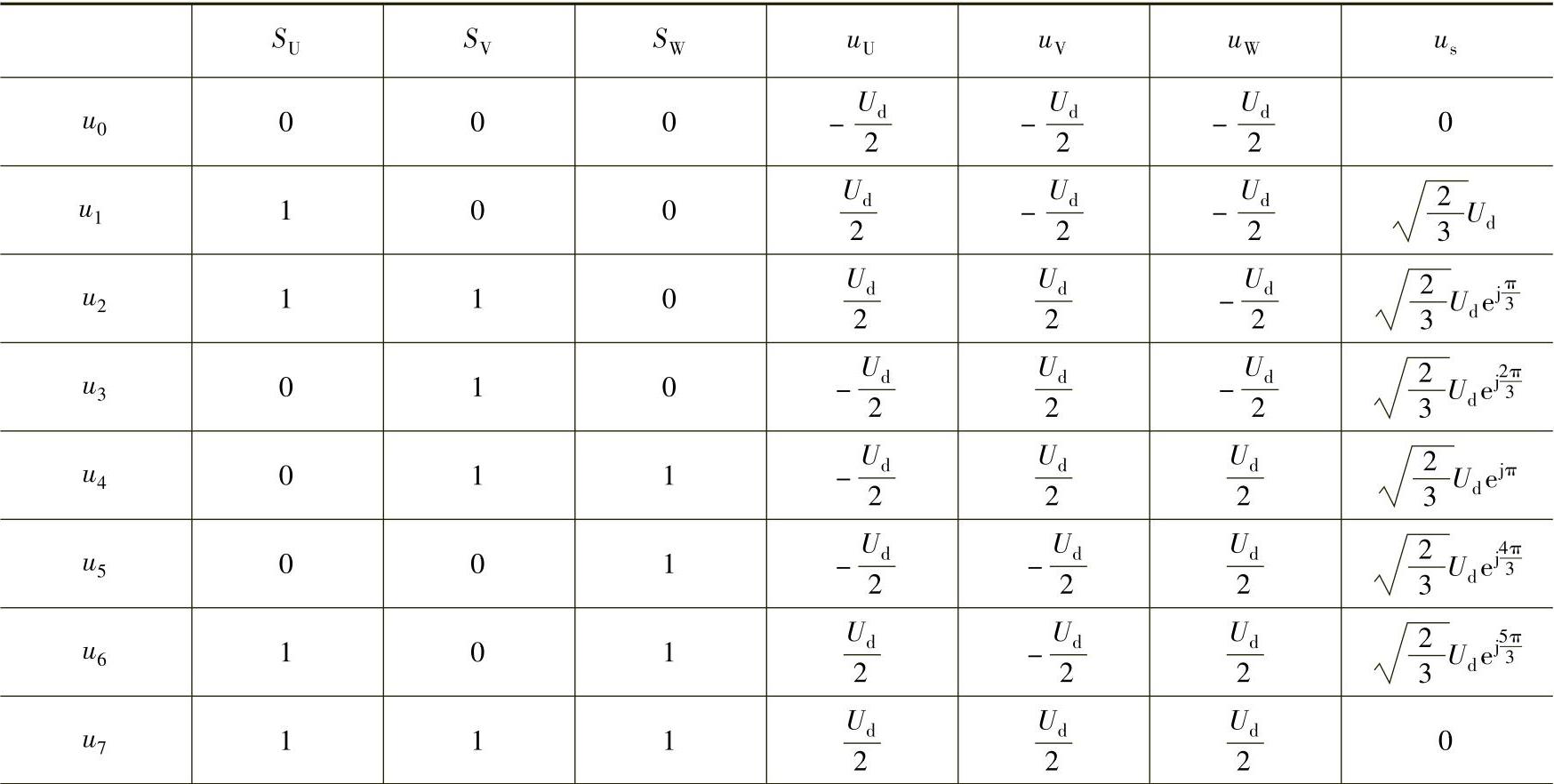
依此类推，可得八个基本空间矢量，见表2-1，其中六个有效工作矢量u₁～u₆，幅值为直流电压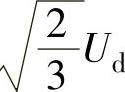，在空间互差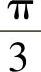，另两个为零矢量u₀和u₇，图2-40为基本电压空间矢量图。

表2-1 基本空间电压矢量

4.正六边形空间旋转磁场

令六个有效工作矢量按u₁～u₆的顺序分别作用Δt时间，并使

也就是说，每个有效工作矢量作用π/3弧度，六个有效工作矢量完成一个周期，输出基波电压角频率。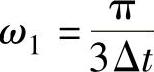

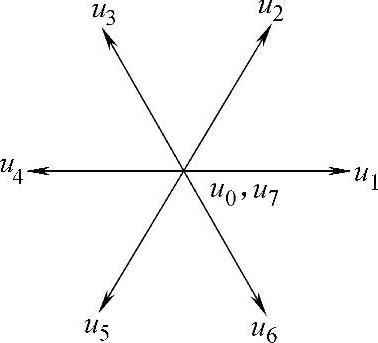
图2-40 基本电压空间矢量图

在Δt时间内，u_s保持不变，式（2-77）可以用增量式表达为

根据式（2-84）可知，定子磁链矢量的增量为

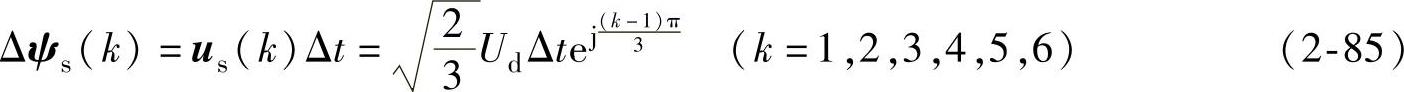
定子磁链矢量运动方向与电压矢量方向相同，增量的幅值等于电压矢量的幅值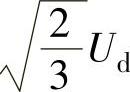与作用时间Δt的乘积，定子磁链矢量的运动轨迹为

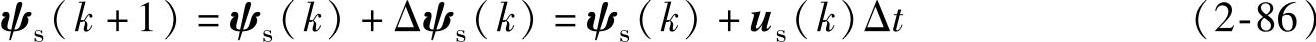
图2-41所示为定子磁链矢量增量Δψ_s（k）与电压矢量u_s（k）和时间增量Δt的关系。

在一个周期内，六个有效工作矢量顺序各作用一次，将六个Δψ_s（k）首尾相接，定子磁链矢量是一个封闭的正六边形，如图2-42所示。由正六边形的性质可知

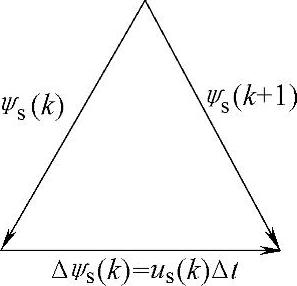
图2-41 定子磁链矢量增量Δψ_s（k）与电压矢量u_s（k）和时间增量Δt的关系

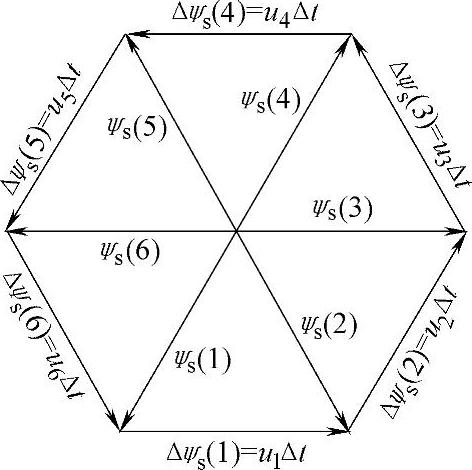
图2-42 正六边形定子磁链轨迹(https://www.xing528.com)

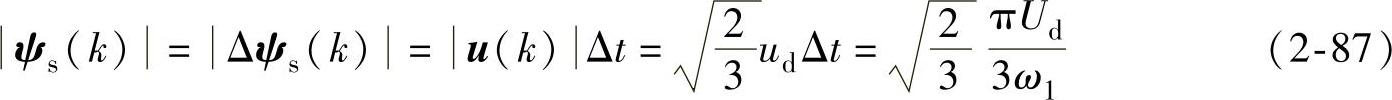
式（2-87）表明，正六边形定子磁链的大小与直流侧电压U_d成正比，而与电源角频率成反比。在基频以下调速时，应保持正六边形定子磁链的最大值恒定。若直流侧电压U_d恒定，则ω₁越小时，Δt越大，势必导致|ψ_s（k）|增大。因此，要保持正六边形定子磁链不变，必须使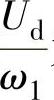为常数，这意味着在变频的同时必须调节直流电压U_d，从而造成了控制的复杂性。

要解决以上问题，有效的方法是插入零矢量，由式（2-84）可知，当零矢量u_s=0作用时，定子磁链矢量的增量Δψ_s=0，表明定子磁链矢量ψ_s停留不动。如果让有效工作矢量的作用时间为Δt₁＜Δt，其余的时间Δt₀=Δt-Δt₁用零矢量来补，当ω₁Δt=ω₁（Δt₁+Δt₀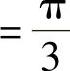）时，在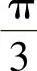弧度内定子磁链矢量的增量为

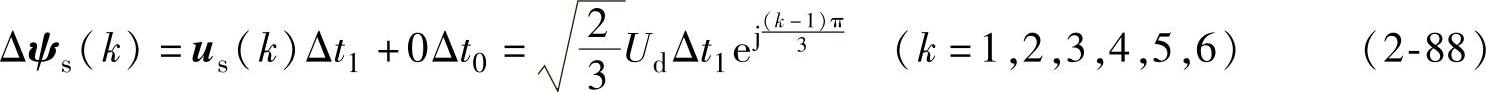
在Δt₁时间段内，定子磁链矢量轨迹沿着有效工作电压矢量方向运行，在Δt₀时间段内，零矢量起作用，定子磁链矢量轨迹停留在原地，等待下一个有效工作矢量的到来。

正六边形定子磁链的最大值为

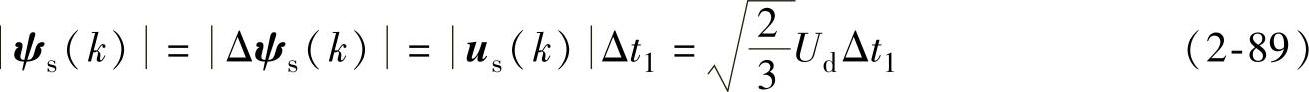
在直流电压U_d不变的条件下，要保持ψ_s（k）恒定，只要使Δt₁为常数即可。电源角频率ω₁越低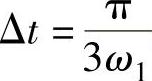，越大，零矢量作用时间Δt₀=Δt-Δt₁也越大，定子磁链矢量轨迹停留的时间越长。由此可知零矢量的插入有效地解决了定子磁链矢量幅值与旋转速度的矛盾。

5.期望电压空间矢量的合成

每个有效工作矢量在一个周期内只作用一次的方式只能生成正六边形的旋转磁场，与在正弦波供电时所产生的圆形旋转磁场那个相差甚远，六边形旋转磁场带有较大的谐波分量，这将导致转矩与转速的脉动。要获得更多边形或接近圆形的旋转磁场，这就必须有更多的空间位置不同的电压空间矢量以供选择，但PWM逆变器只有八个基本电压矢量，能否用这八个基本矢量合成其他多种不同的矢量呢？答案是肯定的，按空间矢量的平行四边形合成法则，用相邻的两个有效工作矢量合成期望的输出矢量，这就是电压空间矢量PWM（SVP-WM）的基本思想。

按六个有效工作矢量将电压空间矢量分为对称的六个扇区，如图2-43所示，每个扇区对应π/3，当期望输出电压矢量落在某个扇区内时，就用与期望输出电压矢量相邻的两个有效工作矢量等效地合成期望输出矢量。所谓等效是指在一个开关周期内，产生的定子磁链的增量近似相等。

以在第Ⅰ扇区内的期望输出矢量为例，图2-44表示由基本电压空间矢量u₁和u₂的线性组合构成期望的电压矢量u_s，θ为期望输出电压矢量与扇区起始边的夹角。在一个开关周期T₀中，u₁作用时间为t₁，u₂的作用时间为t₂，按矢量合成法则可得

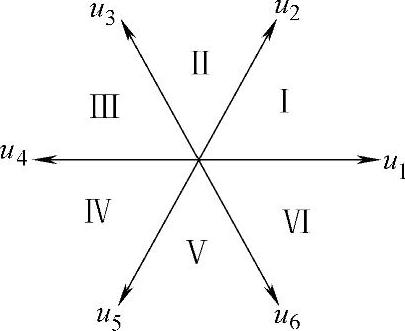
图2-43 电压空间矢量的六个扇区

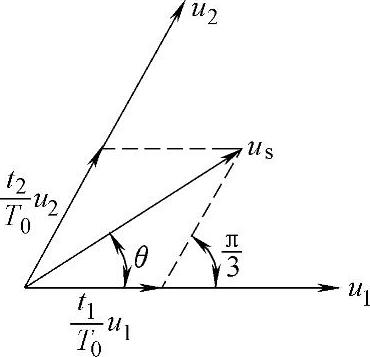
图2-44 期望输出电压矢量的合成

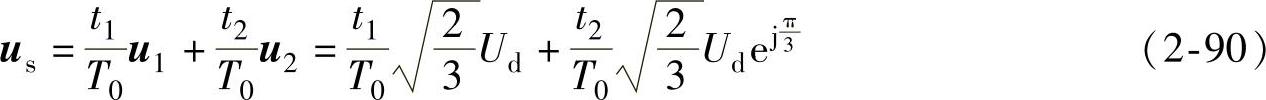
由正弦定理可得

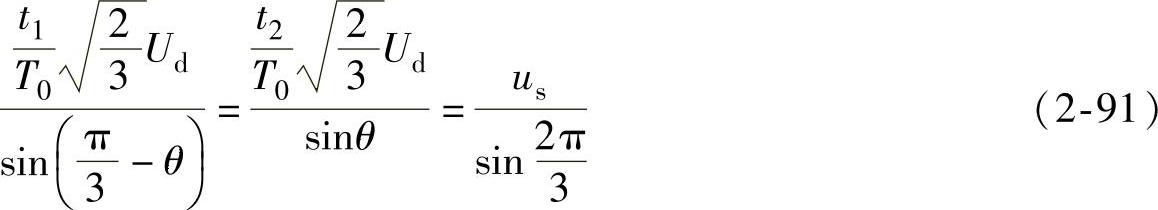
由式（2-91）解得

一般来说t₁+t₂＜T₀，其余的时间可用零矢量u₀或u₇来填补，零矢量的作用时间为

t₀=T₀-t₁-t₂ （2-94）

两个基本矢量作用时间之和应满足

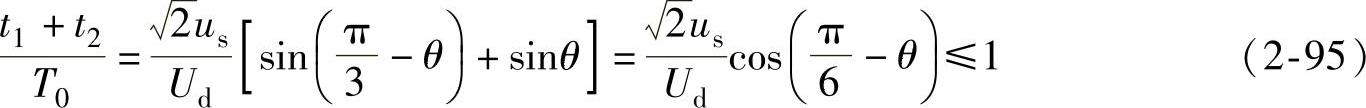
由式（2-95）可知，当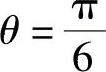时，t₁+t₂＜T₀最大，输出电压矢量最大幅值为

由式（2-75）可知，当定子相电压u_UO、u_VO、u_WO为三相平衡正弦电压时，三相合成矢量幅值是相电压幅值的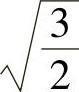倍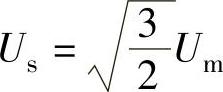，，故基波相电压最大幅值可达

基波线电压最大幅值为

而SPWM的基波线电压最大幅值为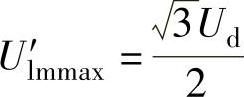，两者之比为

因此，SVPWM方式的逆变器输出线电压基波最大值为直流侧电压，比SPWM逆变器输出电压最多提高了约15%。由于扇区的对称性，以上的分析可以推广到其他各个扇区。

6.SVPWM的实现方法

由期望输出电压矢量的幅值及位置可确定相邻的两个基本电压矢量以及它们作用时间的长短，并由此得出零矢量的作用时间的大小，但尚未确定它们的作用顺序。这就给SVPWM的实现留下了很大的余地，通常以开关损耗和谐波分量都较小为原则，来安排基本矢量和零矢量的作用顺序，一般在减小开关次数的同时，尽量使PWM输出波形对称，以减少谐波分量。下面以第Ⅰ扇区为例，介绍两种常用的SVPWM实现方法。

（1）零矢量集中的实现方法

按照对称原则，将两个基本电压矢量u₁、u₂的作用时间t₁、t₂平分为二后，安放在开关周期的首端和末端，把零矢量的作用时间放在开关周期的中间，并按开关次数最少的原则选择零矢量。

图2-45给出了两种零矢量集中的SVPWM的实现：图2-45a的作用顺序为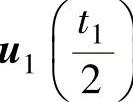、、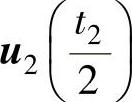u₇（t₀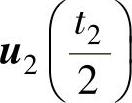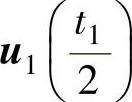）、、，在中间选用零矢量u₇；图2-45b的作用顺序为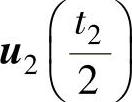、、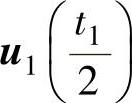u₀（t₀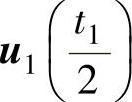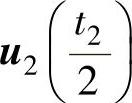）、、，在中间选用零矢量u₀。

由图2-45可知，在一个开关周期内，有一相的状态保持不变，始终为“1”或“0”，从一个矢量切换到另一个矢量时，只有一相状态发生变化，因此开关次数少，开关损耗小。用于电动机控制的DSP集成了SVPWM方法，能根据基本矢量的作用顺序和时间，按照开关损耗最小的原则，自动选取零矢量，并确定零矢量的作用时间，大大减少了软件的工作量。

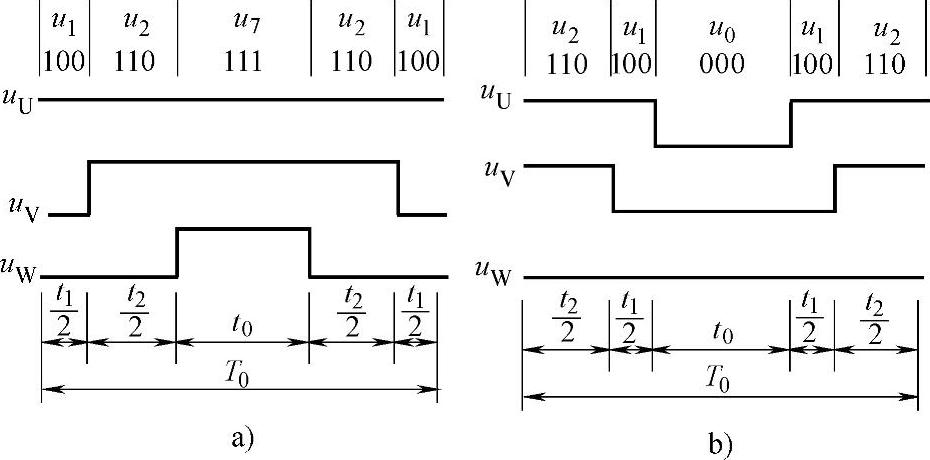
图2-45 零矢量集中的SVPWM实现

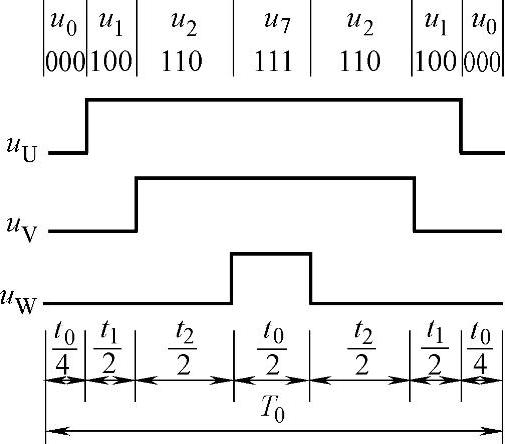
图2-46 零矢量分散的SVPWM实现

（2）零矢量分散的实现方法

将零矢量平均分成四份，在开关周期的首、尾各放一份，在中间放两份，将两个基本电压矢量u₁、u₂的作用时间t₁、t₂平分为二后，插在零矢量间，按开关损耗较小的原则，首、尾的零矢量取u₀，中间的零矢量取u₇。SVPWM的顺序和作用时间为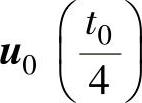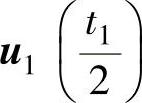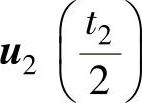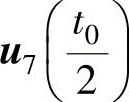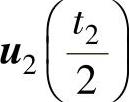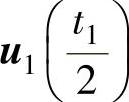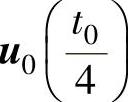：、、、、、、，如图2-46所示。

这种实现方法的特点是：每个周期均以零矢量开始，并以零矢量结束，从一个矢量切换到另一个矢量时，总有一相状态发生变化，但在一个开关周期内，三相状态均各变化一次，开关损耗略大于零矢量集中的方法。

7.SVPWM控制的定子磁链

将占据π/3的定子磁链矢量轨迹等分为N个小区间，每个小区间所占的时间为T₀=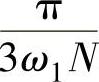，则定子磁链矢量轨迹为正6N边形，与正六边形的磁链矢量轨迹相比较，正6N边形轨迹更接近于圆，谐波分量小，能有效减小转矩脉动。图2-47是N=4时期望的定子磁链矢量轨迹，在每个小区间内，定子磁链矢量的增量为Δψ_s（k）=u_s（k）T₀，由于u_s（k）非基本电压矢量，必须用两个基本矢量合成。图中在定子磁链矢量ψ_s（0）顶端绘出六个工作电压空间矢量，可以看出，施加不同的电压矢量将产生不同的磁链增量，由于六个电压矢量的方向不同，不同的电压作用后产生的磁链变化也不一样。

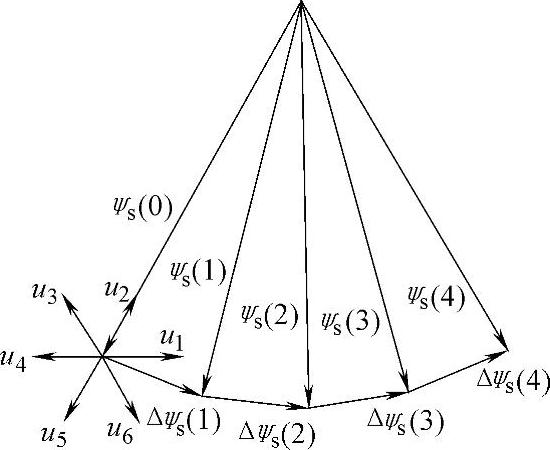
图2-47 N=4时期望的定子磁链矢量轨迹

由图2-47可以看出，当k=0时，为了产生Δψ_s（0），u_s（0）可用u₆和u₁合成，即

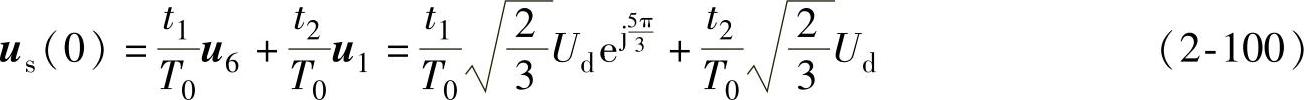
则定子磁链矢量的增量为

采用零矢量分布的实现方法，按开关损耗较小的原则，各基本矢量作用的顺序和时间为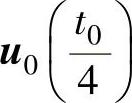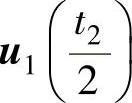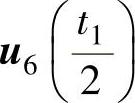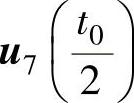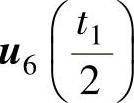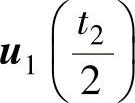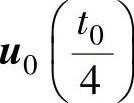：、、、、、、。因此，在T₀时间内，定子磁链矢量的运动轨迹分7步完成，即

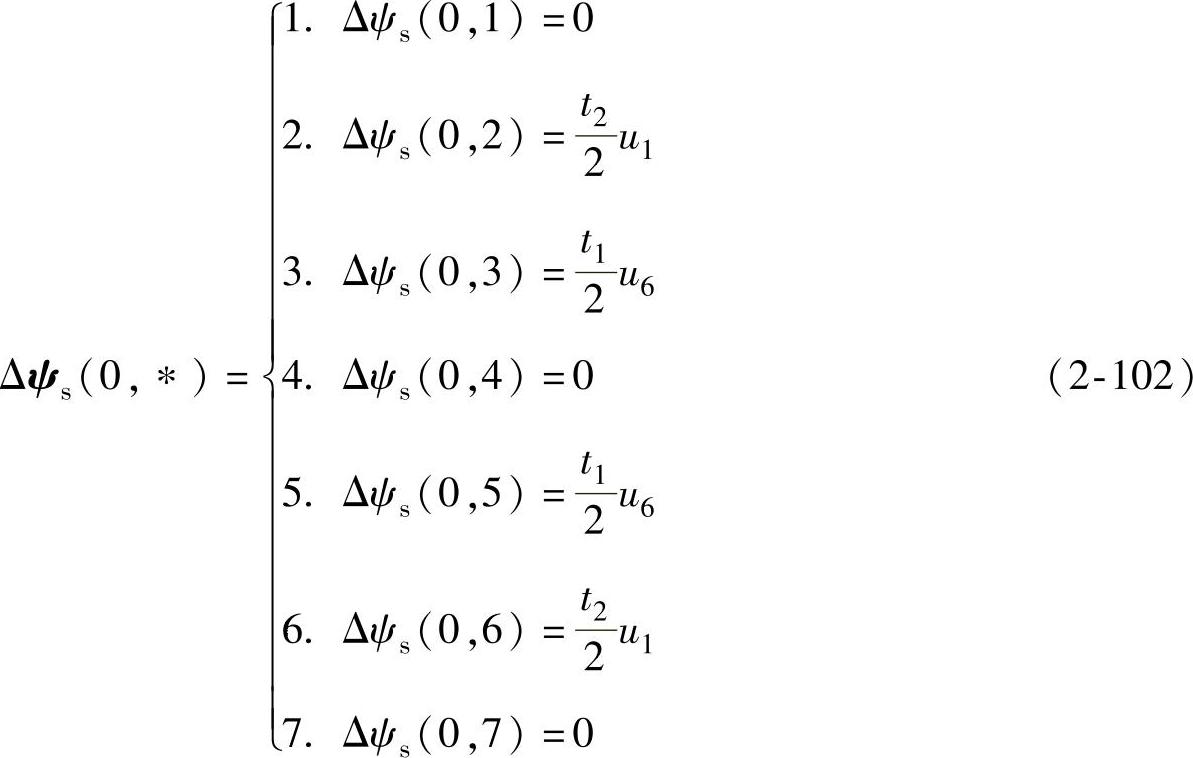
由式（2-102）可知，当Δψ_s（0，*）=0时，定子磁链矢量停留在原地，Δψ_s（0，*）≠0时，定子磁链矢量沿着电压矢量的方向运动，如图2-48所示。

对于Δψ_s（1）的分析方法与Δψ_s（0）相同，对于Δψ_s（2）与Δψ_s（3），需要用u₁和u₂合成，图2-49是在N=4时π/3弧度内实际的定子磁链矢量轨迹。

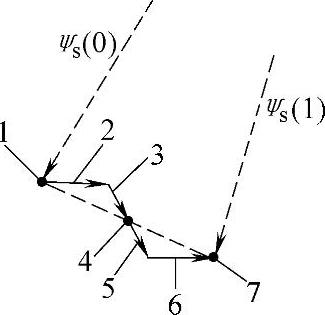
图2-48 定子磁链矢量运动的7步轨迹

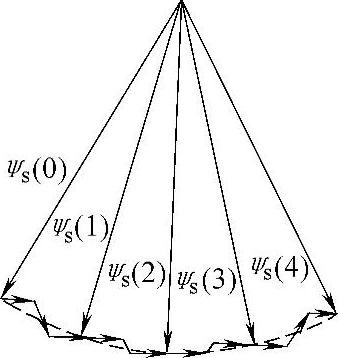
图2-49 N=4时π/3弧度内实际的定子磁链矢量轨迹

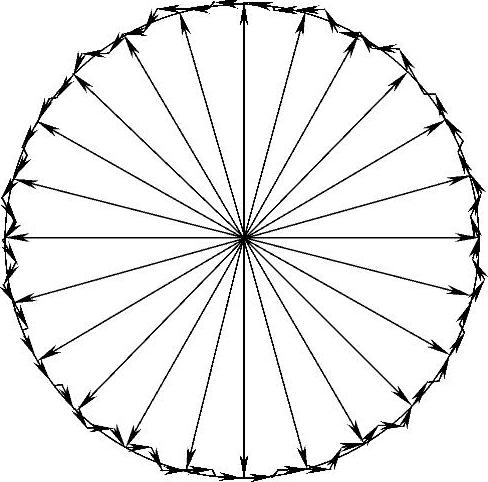
图2-50 定子磁链矢量轨迹

当磁链矢量位于其他的π/3区域内时，可用不同的基本电压矢量合成期望的电压矢量。图2-50是定子磁链矢量在0～2π的轨迹，实际的定子磁链矢量轨迹在期望的磁链周围波动。N越大，T₀越小，磁链轨迹越接近圆，但开关频率随之增大。由于N是有限的，所以磁链轨迹只能接近于圆，而不可能等于圆。

归纳起来，SVPWM控制模式有以下特点：

1）逆变器共有八个基本输出矢量，有六个有效工作矢量和两个零矢量，在一个旋转周期内，每个有效工作矢量只作用一次的方式只能生成正六边形的旋转磁链，谐波分量大，将导致转矩脉动。但由于器件开关次数较少，从而降低了开关损耗。

2）用相邻的两个有效工作矢量，可合成任意的期望输出电压矢量，使磁链轨迹接近于圆。开关周期T₀越小，旋转磁场越接近于圆，但功率器件的开关频率越高。

3）利用电压空间矢量直接生成三相PWM波，计算简便。

4）直流电压利用率高，与一般的SPWM相比较，SVPWM控制方式的输出电压最多可提高15%。