3种SPWM模式的优化方案

1.消除特定谐波法（Selected Harmonlcs Elimination PWM，简称SHEPWM）

消除特定谐波法是在电压波形特定位置上设置缺口，通过每个周期中逆变器的多次换向，恰当地控制逆变器的脉宽调制电压波形，使逆变器输出的电压中不存在某些特定的谐波。

一般来说，在半个周期的电压波形上，每设置一个缺口，就可以消除一种谐波。在选择脉宽调制电压的波形时，必须满足波形的正半周与负半周关于零点对称，每半个周期对π/2轴对称，使波形为奇函数，波形中将不包含余弦项与偶次谐波，这样，波形中的谐波含量才能最少。如图2-26和图2-27所示，假定开关角α_i（i=1，2，…，g）满足以下条件：

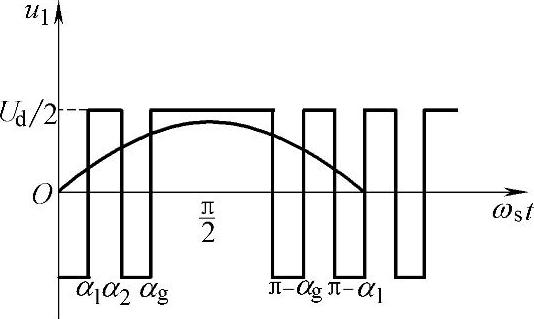
图2-26 一种双极性SPWM波形

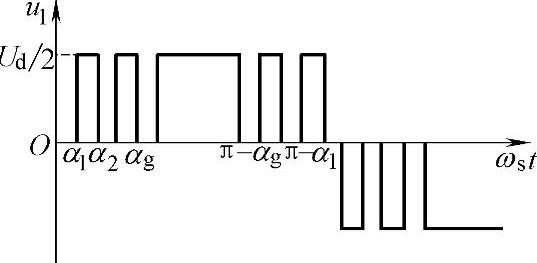
图2-27 一种单极性SPWM波形

0≤α₁≤α₂≤α₃…≤α_g≤π/2同时由于它们是奇函数且关于π/2轴对称，故可以求出它们的n次谐波幅值表达式。

对于图2-26所示波形的表达式为

此处N为一个周期的脉冲数，对于图2-27所示波形的表达式为

此处N为半个周期的脉冲数。

由此可知，各次谐波的幅值是开关角α_i的函数，只要适当地选择α_i（i=1，2，…，g）的值，就可使U_sm（i）=0，亦即消除了频率为iω_s次的谐波。一般情况下，由于电动机的特殊连接形式，使得线电压中不会存在零序谐波，所以重点要消除的谐波为5，7，13，…，6l-1，6l+1，（l=1，2，…）次。令g为1/4周期发出的开关点数，而单位周期的N_CM个调制脉冲可将g-1种谐波消除。对于单极性调制，载波比为2N=2g；对双极性调制，载波比为N=2g+1。

例如，欲消除两种谐波，则1/4周期（π/2）内需设g=2+1=3个开关点，即α₁、α₂、α₃。

若要消除5次、7次这两种谐波，由式（2-42）则有

消除5次谐波

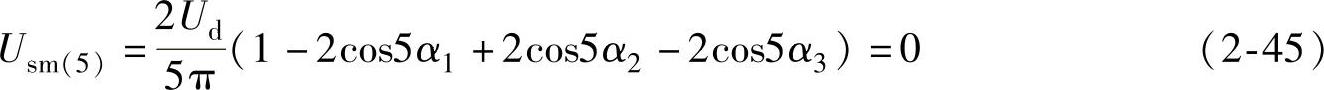
消除7次谐波

随着基波幅值U_sm（1）的变化，式（2-44）、式（2-45）、式（2-46）的α₁、α₂、α₃也变化，所以调整α₁、α₂、α₃的值，使之符合上述三式，就既可以消除5、7次谐波，又可输出所需大小的基波电压。

2.谐波效应最小法（CHMPWM）

消除特定谐波法，是根据要消去的谐波次数，计算开关角度数据。虽然可消除某些特定谐波，但往往是规定的谐波消去了，其他谐波却被放大了。谐波效应最小法与消除特定谐波法的不同之处是，它不是按照消除特定谐波来选择开关角，即不要求某些谐波为零，而是以电流谐波有效值最小来选择开关角的，因而在一些文献中把CHMPWM称为“最优PWM”。此法所用的脉宽调制波形与消除特定谐波法相同，只是选择开关角的出发点不同，所以，此法从某种意义上来说是消除特定谐波法的继续和发展。

对于图2-27及式（2-46）来说，假定电流仅仅由负载电动机的漏抗来决定，并且是线性的，则其n次谐波的漏抗应为nω_sL，谐波电流有效值为

假定

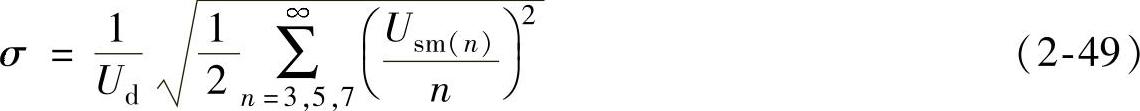
ξ是一个与直流电源U_d有关的常数，σ是一个无量纲的数，它仅仅由开关角α₁，…，α_N来决定。由式（2-47）可知，要使I_（n）最小，实际上也就是使σ的值为最小，故式（2-48）和式（2-49）是以电流谐波有效值为最小来计算开关角α_i的基本方程式。

3.准正弦波脉宽调制法（Suboptimal）

正弦波脉宽调制法，虽然各脉冲面积之和与正弦波下的面积成正比，使其调制波形更接近于正弦波，谐波分量已很小。但一般在正常工作情况下，要求正弦波参考信号u_r的最大幅值U_rm不能大于三角波幅值U_cm，即调制深度m≤1。当m＞1时，正弦脉宽调制波中将出现饱和现象，不但输出电压与频率失去所要求的配合关系，而且输出电压中的谐波分量增大，特别是较低次的谐波分量增加较大，对电动机运行不利。另一方面，可以证明，当采用正弦波脉宽调制时，如调制系数m≤1时，逆变器输出的线电压中基波分量的幅值最大值，只有逆变器输入的电网线电压幅值的0.866倍，使采用正弦波脉宽调制法的系统，不能充分利用逆变器电压容量。这可以通过提高直流电压利用率和减少开关次数的方法来解决这个问题，因此称此法为准正弦波脉宽调制法。准正弦波脉宽调制法就是在正弦参考波u_r上叠加适当幅度与相位的三次谐波分量u_r3，如图2-28所示。使得合成的参考信号u_r′最大值减小，从而可以进一步提高正弦参考波u_r的幅值，即可以使m＞1，这样做虽然会在逆变器输出电压中产生大量三次谐波分量，但由于三相交流电动机负载的连接方式，可使线电流中不出现三次谐波，并不影响电动机的运行。

图2-28 正弦参考波上叠加三次谐波(www.xing528.com)

应在正弦参考信号u_r上叠加多大幅值的三次谐波，才能使其调制系数m尽可能地提高，以充分利用逆变器电压容量，而又不增加谐波的分量呢？推导如下，假设原正弦参考信号u_r为单位正弦波，则合成参考信号u_r′为

u_r′=sinθ+αsin3θ （2-50）

式中，θ=ω_st，α为待定系数。

将u_r′对θ微分，并使其为零，可找出极值点，即

利用恒等式cos3θ=4cos³θ-3cosθ，由式（2-51）可求得极值点发生在

再利用sin²θ+cos²θ=1这一恒等式，从式（2-53）求得

利用恒等式sin3θ=3sinθ-4sin³θ，可求出u_r′的峰值U′_rm为

把式（2-54）代入式（2-55）得

α的最佳值就是在U′_rm的极值处，因此可通过对U′_rm表达式进行微分，并使其为零得到。

由式（2-57）可求得

及

另外，由式（2-52）得

sinθ=1 （2-60）

将式（2-60）代入式（2-55）得

从式（2-61）可以看出，α为负值时，U′_rm大于1，因此可以舍掉α=-1/3，因而所要求的α值为1/6。所需要的综合后的最佳参考信号u_r′为

将式（2-59）代入式（2-53）可求得

将式（2-63）代入式（2-64）可求得参考信号u_r′的峰值为

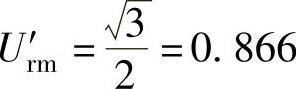
可见，在正弦参考信号u_r上叠加正弦基波的1/6幅值的三次谐波，其结果是按0.866的系数降低了u_r波形的幅值。按系数k增加调制正弦基波的幅值，以重新利用逆变器的满输出电压，为此，调制波变为

如果原设计的U′_rm为0.866，则有1=0.866k，即k=1.155。即叠加1/6幅值的三次谐波后，在调制波不发生饱和的条件下，使正弦参考信号u_r的幅值增加15.5%，使m＞1。最终，可使主电路输出相电压基波幅值产生了15.5%的增量。从而使系统在不增加谐波分量的条件下，又充分利用了逆变器主电路的输出电压，使得逆变输出电压几乎等于电源送给逆变器的电压。