电压正弦PWM控制技术：SPWM逆变器

图2-17 用SPWM电压等效正弦电压

a）正弦电压 b）SPWM等效电压

1.电压正弦波脉宽调制法

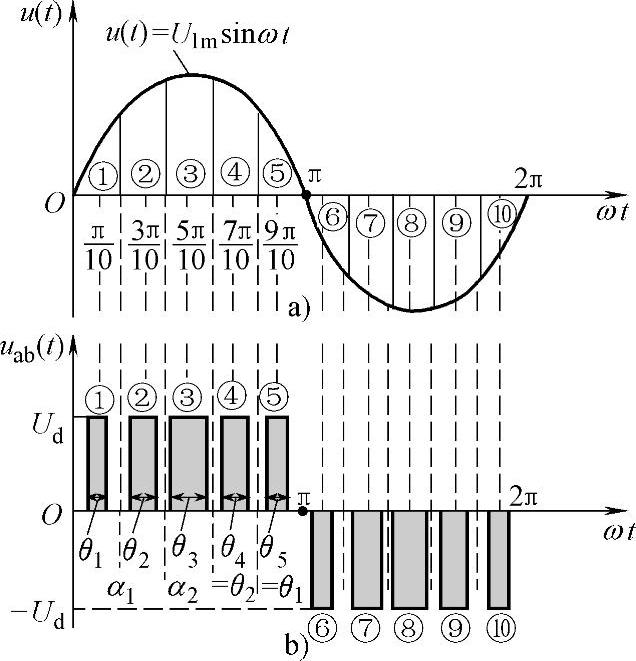
在采样控制理论中有一个重要理论，冲量（窄脉冲的面积）相等而形状不同的窄脉冲加在具有惯性的环节上时，其效果基本相同（环节的输出响应波形基本相同即响应波形傅里叶分解后，其低频段特性非常接近，仅在高频段略有差异）。该结论是PWM控制技术的重要理论基础。

对于电压正弦PWM，可以把电压正弦波分为N等份，如图2-17a所示（图中N=10），然后把每一份的正弦曲线与横轴所包围的面积都用一个与此面积相等的等高矩形脉冲来代替，矩形脉冲的中点与正弦波每一等份的中点重合。这样，由N个等幅而不等宽的矩形脉冲所组成的波形就与正弦波等效。

图2-17b所示的一系列等幅不等宽的矩形脉冲波形，就是所希望逆变器输出的SPWM波形。由于每个脉冲的幅值相等，所以逆变器可由恒定的直流电源供电，也就是说，这种交-直-交变频器中的整流器采用不可控的二极管整流器就可以了。当逆变器各功率开关器件都是在理想状态下工作时，驱动相应功率的开关器件的信号也应为与图2-17b形状一致的一系列脉冲波形。

这一系列的脉冲波形的宽度θ可以严格地用计算方法求得，作为控制逆变器中各功率开关器件通断的依据。但较为实用的方法是采用“调制”的方法。以所希望的波形作为调制波，而受它调制的信号成为载波。在SPWM中常用等腰三角波作为载波，因为等腰三角波是上下宽度线性对称变化的波形，当它与一个正弦波曲线相交时，在交点的时刻产生控制信号，用来控制功率开关器件的通断，就可以得到一组等幅而脉冲宽度正比于对应区间正弦波曲线函数值的矩形脉冲。

图2-18a是SPWM变频器的主电路，图中VT₁～VT₆是逆变器的六个IGBT功率开关器件，各有一个续流二极管反并联连接，逆变器所需要的恒值直流电压由三相整流器提供。图2-18b是它的控制电路框图，由参考信号发生器提供一组三相对称可调正弦参考信号u_MU、u_MV、u_MW，其频率决定逆变器输出的基波频率。参考信号的幅值也可在一定的范围内变化，以决定输出电压的大小。三角载波信号u_C是共用的，分别与每相参考电压比较后，给出“正”或“零”的饱和输出，产生SPWM脉冲序列波u_DU、u_DV、u_DW作为逆变器功率开关器件的控制信号。为了方便，设功率开关器件为理想开关，因而当逆变器任一相功率开关器件导通时，电动机绕组上所获得的对直流电源假想中性点N′的电位为U_d/2或-U_d/2。

图2-18 SPWM逆变器电路原理框图

a）主电路 b）控制电路框图

改变参考信号u_M的幅值时，脉宽随之改变，从而改变了逆变器输出电压的大小，当改变u_M的频率时，输出电压频率也随之改变。但一般情况下参考信号u_M的最大幅值必须小于三角波幅值，否则输出电压的大小和频率将失去所要求的配合关系。

2.电压正弦波脉宽调制信号生成方法

（1）单极性三角波调制法

单极性SPWM调制是指参加调制的载波三角波和正弦波参考信号极性不变。

单极性调制时，在正弦波的半个周期内每相只有一个开关器件开通或关断。例如，A相正半周时，在图2-19a中为VT₁的反复通断，图2-19表示了此时的调制情况，当参考电压u_MU高于三角波电压u_C时，相应比较器的输出电压为“正”电平，反之为零电平。只要正弦调制波的最大值小于三角波的幅值，由图2-19a的调制结果必然形成图2-19b所示的等幅不等宽而且中间宽两边窄的SPWM波形。负半波是利用同样的方法调制再经倒相器倒相后形成的。

图2-19d中，由于u′_UN的“正”、“零”两种电平分别对应于功率开关器件VT₁的通和断两种状态；“负”和“零”两种电平分别对应于功率开关器件VT₄的通和断两种状态。由于VT₁、VT₄在正、负半周内反复通断，故在逆变器的输出端可获得重现u′_DU形状的相电压u′_UN=f（U），其幅值为U_d/2，其宽度按正弦规律变化，如图2-19e所示。B、C两相的相电压u′_VN、u′_WN的获得方法与此相同。

图2-19 单极性脉宽调制波形

a）正弦调制波与三角载波 b）u_DU=f₀（ω_sV） c）倒相信号 d）u′_DU=f₁（ω_sV） e）u′_UN=f₂（ω_sV）

（2）双极性三角波调制法

双极性SPWM调制指载波三角波和正弦波参考信号是具有正负极性变化的信号。

图2-20b中调制参考波为幅值为U_rm的正弦波u_r，其频率f_M就是输出电压基波频率f₁。高频载波为双极性三角波u_c，其幅值为U_cm，频率为f_c。无论正弦波u_r在正半周还是负半周，当瞬时值u_r＞u_c时，给VT₁和VT₄导通信号，U_G1＞0，U_G4＞0。同时，给VT₂和VT₃关断信号，使U_G2、U_G3为负值，VT₂、VT₃截止，此时逆变器输出电压u_o=U_d；当瞬时值u_r＜u_c时，使VT₁、VT₄截止，VT₂、VT₃的驱动信号U_G2、U_G3为正值，VT₂、VT₃导通，逆变器输出电压u_o=-U_d。

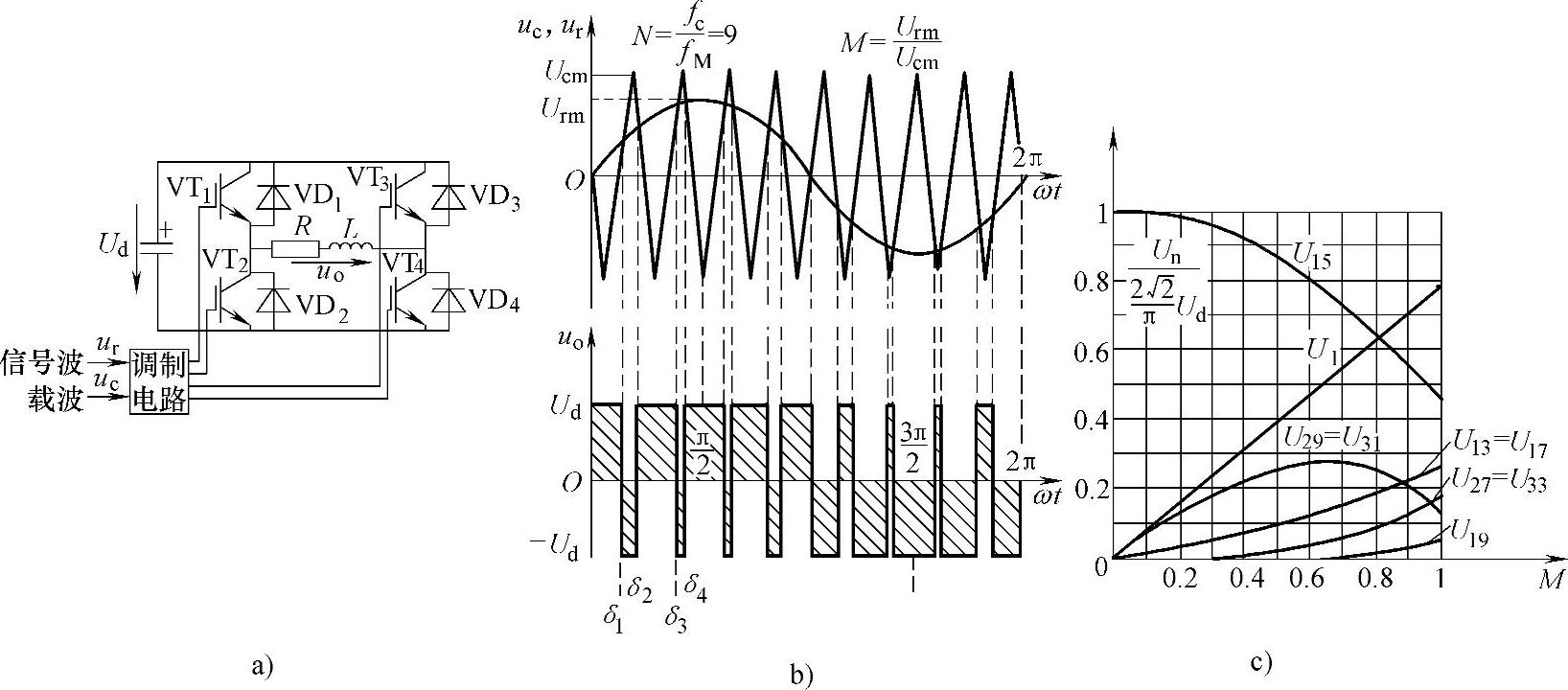
图2-20 双极性SPWM调制原理及其输出波形

a）主电路 b）电压波形 c）N_CM=15，基波和谐波值

图2-20b中的输出电压u_o，由多个不同宽度的双极性脉冲电压方波组成。载波比N=f_c/f_M=f_c/f₁，则每半个周波中正脉冲和负脉冲共有N个。若固定三角波载波频率f_c，改变f_M，即可改变输出交流电压基波的频率f₁（f₁=f_M）。固定三角载波电压幅值U_cm，改变正弦调制参考波u_r的幅值U_rm，即改变调制比M（M=U_rm/U_cm，U_rm=MU_cm）则将改变u_r与u_c两波形的交点，从而改变每个脉冲电压的宽度，改变u_o中的基波和谐波的数值。图2-20b中的输出电压在正负半周都有多个正、负脉冲电压，故称为双极性SPWM调制。可以证明，如果载波比N足够大，调制比M≤1，则基波电压幅值U_1m≈MU_d=U_dU_rm/U_cm，输出电压基波

最大时其有效值只能达到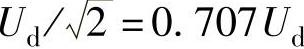，这与单极性SPWM控制是一样的。

图2-20c画出了N=15时的双极性SPWM控制的基波和各次谐波的相对值随电压调制系数M=U_rm/U_cm而改变的特性曲线。图中纵坐标基准值取为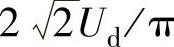，分析计算得知双极性SPWM控制时输出电压中可以消除N-2次以下的谐波。因此除基波外，其最低阶次的谐波为N-2次。例如N=15时最低次谐波为13次。15次谐波最大，。如果逆变器输出频率f₁=50Hz，开关的通、断频率f_k=2kHz，则N=2000/50=40，这时可以消除38次以下的谐波。存留的谐波由于阶次高，容易滤除，其相应的畸变系数是很小的。

3.正弦波脉宽调制信号的调制方式

在SPWM逆变器中，载波频率f_c与调制波频率f_M（逆变器输出的基波频率）之比N=f_c/f_M称为载波比。对于单极性调制而言，由于一个周期内有2N个脉冲，则载波比为2N；而双极性调制由于一个周期内有N个脉冲，则载波比为N。根据载波比的变化与否，SPWM逆变器可以有同步调制和异步调制两种调制方式。而为了使输出波形保持三相对称且谐波少，可采用同步调制与异步调制相结合的分段同步调制。

（1）同步调制

载波比N等于常数，即在变频时使载波信号的频率与调制波信号的频率保持同步变化的调制方式称为同步调制。在该调制方式中，调制波信号频率变化时载波比N不变，因而，逆变器输出电压半个周期内的矩形脉冲数是固定的。在三相PWM逆变器中取N为3的整数倍，以使三相输出波形严格对称。同时，为了使一相波形正负半周对称，N应取为奇数。

当逆变器输出频率很低时，由于在半周期内输出脉冲数目是固定的，所以，相邻两脉冲的间距增大，谐波会显著增加，使负载电动机产生较大的脉动转矩和较强的噪声，给电动机的工作带来不利影响。

（2）异步调制

为了消除上述同步调制的缺点，可以采用异步调制方式。这种载波信号和调制波信号不保持同步关系的调制方式称为异步调制。在异步调制方式中，在逆变器的整个变频范围内，载波比N是不等于常数的。一般在改变调制波信号频率f_M时保持三角波频率f_c不变，因而，提高了低频时的载波比，这样逆变器输出电压半周期内的矩形脉冲数可随输出频率的降低而增加，相应地减少负载电动机的转矩脉动和噪声，改善了低频工作特性。

异步调制在改善低频特性的同时，又会失去同步调制的优点，当载波比随输出频率的改变而连续变化时，势必使逆变器输出电压的波形及其相位都发生变化，很难保持三相输出间的对称关系。另一方面，当逆变器输出频率增高时，载波比会减小，半周期内输出脉冲的数目减少，输出脉冲的不对称性影响就变大，同时，输出波形和正弦波之间的差异也变大，从而使输出特性变坏，引起电动机工作的不平稳。

为了扬长避短，可将同步和异步两种调制方式结合起来，成为分段同步的调制方式。

（3）分段同步调制

在一定的频率范围内，采用同步调制，保持输出波形对称的优点。当频率降低较多时，使载波比分段有级地增加，又发挥了异步调制的优势，这就是分段同步调制方式。具体地说，将逆变器输出的整个变频范围划分为若干段，在每个频段内都保持载波比N为恒定，不同频段载波比不同。在输出频率的高频段，采用较低的载波比使载波频率不致过高，以满足功率开关器件对开关频率的限制。在输出频率为低频段时，采用较高的载波比，以使载波频率不致过低而对负载产生不利影响。

载波比N值的选取与逆变器的输出频率、功率开关器件的允许工作频率及所采用的控制手段都有关系。为了使逆变器的输出波形更接近于正弦波形，应尽可能增大载波比，但从逆变器本身来看，载波比又不能太大，应受到限制。即(www.xing528.com)

4.SPWM波生成方法

SPWM波就是根据三角载波与正弦调制波的交点而得到的一系列脉冲，其幅值不变而宽度按正弦规律变化。SPWM波可以通过采用模拟电路生成SPWM波形、采用已有集成电路产生SPWM波形或采用微处理器生成SPWM波形。

（1）自然采样法

在载波三角波与调制正弦波的自然交点时刻控制功率开关器件的通断，这种生成SPWM的方法称为自然采样法。由于正弦波在不同相位角时其幅值不同，因而与三角波相交所得到的脉冲宽度也不同。另外，当正弦波频率变化或幅值变化时，各脉冲的宽度也相应变化。故要准确生成SPWM波就要准确地计算出正弦波与三角波的交点，即功率开关器件的导通时刻t_A和关断时刻t_B，功率开关导通的区间就是脉冲宽度t_pu，其关断区间就是脉冲的间隙时刻t_off及t′_off，如图2-21所示。

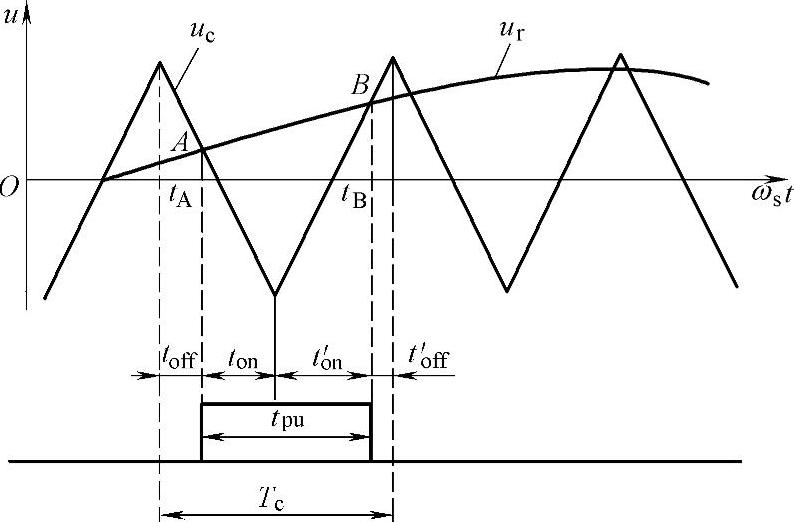
图2-21 生成SPWM波的自然采样法

由图2-21的几何关系可得

式中，除ω_s、T_c、m为已知外，t_A、tB都是未知，该式是一个超越方程，求解时需花费较多的计算时间。可见，自然采样法虽然能真实反应脉冲产生与结束的时刻，却难以在实时控制中在线实现。当然也可以事先把计算出的数据存入计算机中，控制时利用查表法来获取数据。这样做要占用较多的内存空间。所以，此法仅适用于范围有限的场合。

（2）规则采样法

规则采样法是利用载波三角波的正峰值点、负峰值点所对应的正弦函数值来代替三角波与正弦波自然交点处正弦函数值这一规则求取脉冲宽度来生成SPWM波的方法。在规则采样法中，每个载波周期的开关点都是确定的。

依据脉冲是否以相应的三角波峰值点为对称，规则采样法可分为对称规则采样法及不对称规则采样法。

1）对称规则采样法。

在三角波的一个周期内，只利用三角波的一个峰值点所对应的正弦函数值求取的脉冲以三角波的峰值点为对称，因此这种采样方法为对称规则采样法，如图2-22a所示。

这样，一周（2π）内第i个脉冲宽度为

一周（2π）内第i个脉冲的关断时间为

其中ω_s=2πfM

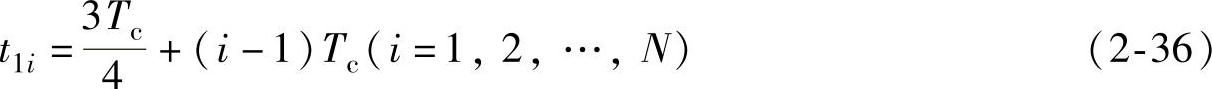
在实际控制中，根据控制中所需的m及ω_s值可实时计算出各相脉宽时间及间隙时间。而波形的获取可利用微机控制系统的定时器中断功能，向接口电路送出相应的高电平、零电平，以此控制开关器件的通断形成SPWM波。对于开环控制系统，在某一给定转速下其m与ω_s值都有确定值，宜采用查表法；对于闭环控制系统，在系统运行中其m与ω_s值随时被调整，宜采用实时计算法。

2）不对称规则采样法。

在三角波的一个周期内，利用三角波的两个峰值点所对应的正弦函数值求取的脉冲对三角波的峰值点不对称，因此这种采样方法为不对称规则采样法，如图2-22b所示。

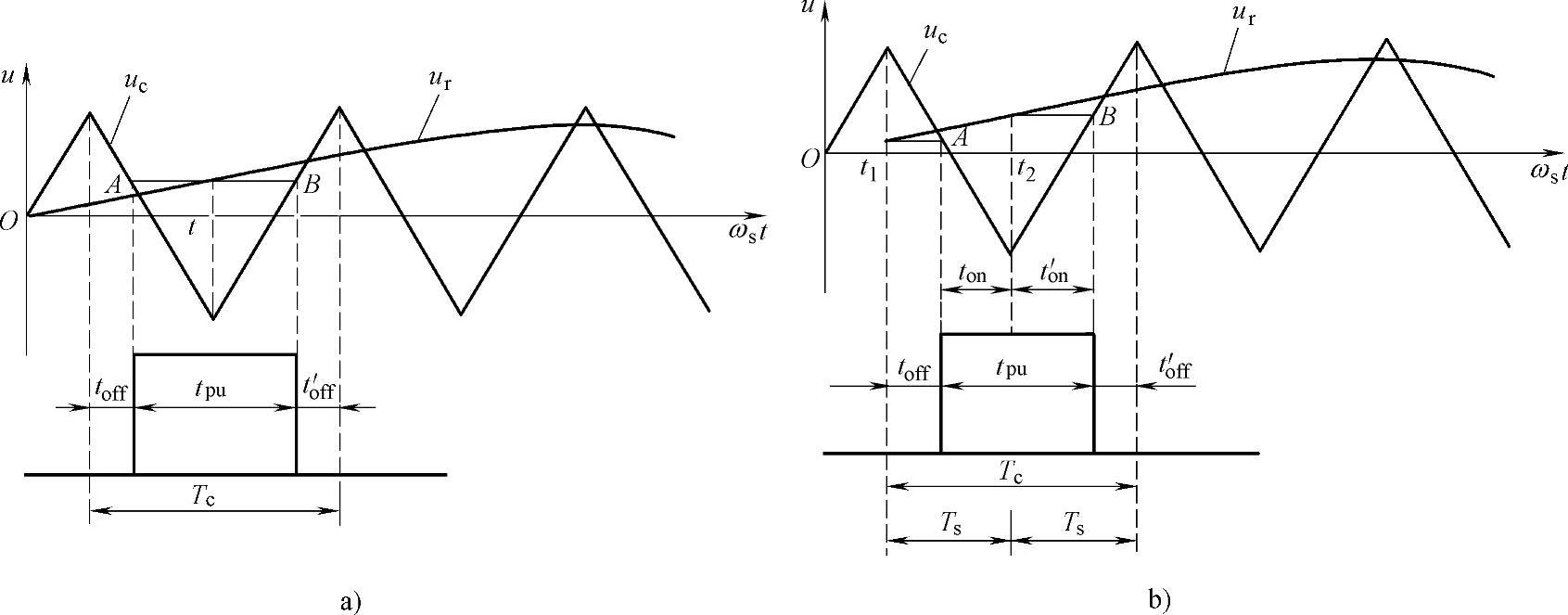
图2-22 生成SPWM波的规则采样法

a）对称规则采样法生成SPWM波 b）不对称规则采样法生成SPWM波

由图2-22b的几何关系有

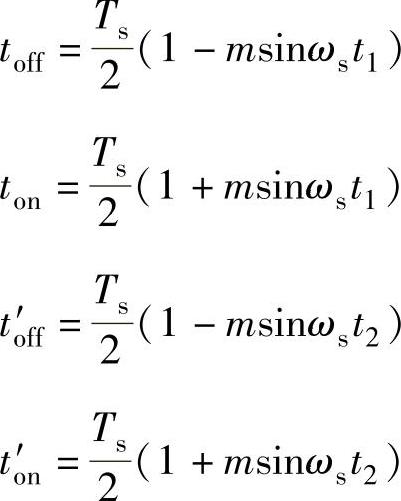
脉冲宽度为

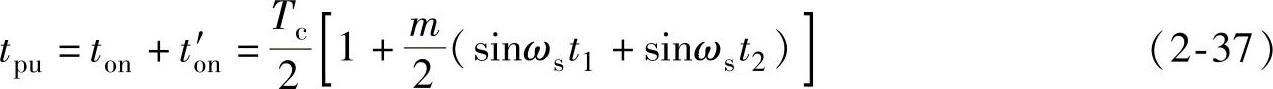
这样，一周期（2π）内第i脉冲的宽度为

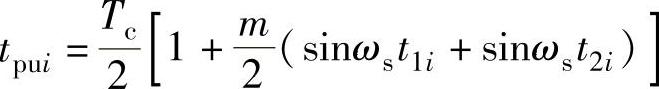
一周期（2π）内第i脉冲的关断时间为

而

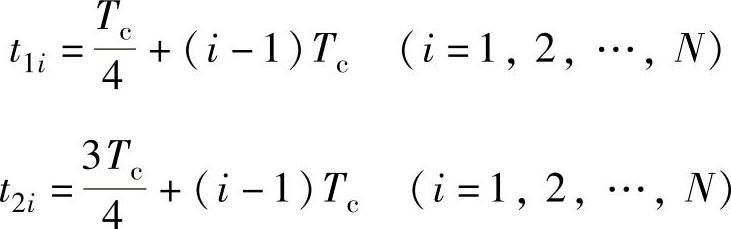
这样

由图2-22a与图2-22b的对比可见，不对称规则采样法所形成的SPWM波更接近于正弦波，因而谐波分量的幅值更小。