回转体的尺寸标注的分析介绍

由回转体的形成可知，回转体的尺寸标注应分为径向尺寸标注和轴向尺寸标注。标注尺寸时，应先标注反映回转体端面图形圆的直径，标注时须在前面加上符号“φ”，然后再标注其长度，如图3-16所示。

回转体的尺寸标注，也可采用集中标注的方法，即将其各种尺寸集中标注在某一视图上，以减少组合体的视图数目。圆球尺寸集中标注时，只需标注出其径向尺寸即可，但须在直径符号前加注“S”，如图3-17所示。

图3-16　回转体的尺寸标注

(a)圆柱;(b)圆锥;(c)圆台

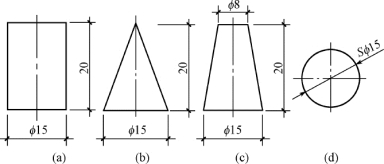
图3-17　回转体尺寸集中标注

(a)圆柱;(b)圆锥;(c)圆台;(d)圆球

典型案例

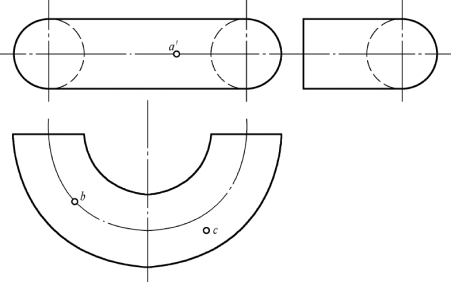
【案例1】　如图3-18所示，已知点M 的正面投影点m′为可见点的投影，求点M 在水平投影面和侧面投影面的位置。

【分析】　由已知条件可以分析出，点M 必定在前半个圆柱面上，其水平投影必定落在具有积聚性的前半个柱面的水平投影图上。

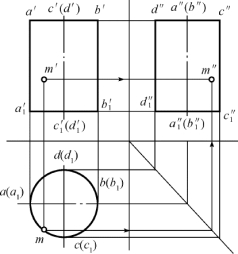
图3-18　圆柱表面上补点

【作图】　由分析可知，点M 位于圆柱面的前面，通过“长对正”，可求解出水平投影面中的点m，再依据“高平齐，宽相等”求解出点m″，如图3-18所示。

【案例2】　在圆锥表面上补点，图3-19中点A 为圆锥表面上一点，已知水平投影面中点a的位置，求另外两个投影面中点a′与点a″。

【分析】　因为圆锥面的三个投影都没有积聚性，所以不能利用积聚性直接在圆锥面上求点，可以利用素线法和辅助平面法求得。

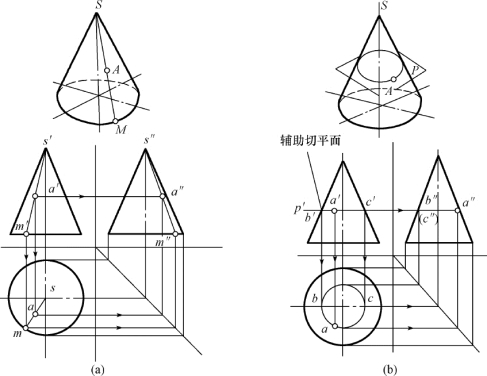
图3-19　圆锥表面上补点(www.xing528.com)

(a)素线法;(b)辅助平面法

【作图】

(1)素线法，如图3-19(a)所示，先过点A 作素线SM 的水平面投影，然后求出s′m′和s″m″，在s′m′和s″m″上求出a′和a″。

(2)辅助平面法，如图3-19(b)所示，过点A 作一直径为BC 的辅助圆P。该圆的正面投影与侧面投影为一条与轴线垂直的直线，它与圆锥轮廓素线的两个交点之间的距离，即圆的直径。通过“长对正，高平齐，宽相等”求出a′与a″。

【案例3】　如图3-20(a)所示，已知球面上点K 的V 面投影为k′，求点k与点k″。

【分析】　作球体表面上的点只能利用辅助平面法，因为球体表面上没有直线。

从图3-20可知，点K 的位置是在上半球面上，又属左半球面，同时又在前半球面上。

图3-20　球体表面上点的投影

(a)已知条件;(b)作图过程

【作图】　作图可用纬圆法。如图3-20(b)所示，过点k′作纬圆的V 面投影1′2′，以1′2′的1/2为半径，以O 为圆心，作纬圆的水平投影(圆)，过点k′引铅垂连线求得点k，再按“三等”关系求得点k″。最后分析可见性，由于点K 在球面的左、前、上方，故三个投影均为可见。

实际演练

1.求作圆锥面上的点的其余两面投影。

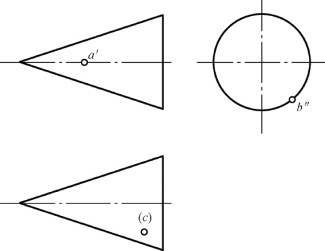
2.求作圆球表面上的点的其余两面投影。

3.求作圆环表面上的点的其余两面投影。