如何用等分圆周作出正多边形

(1)正三角形。

1)用圆规和三角板作圆的内接正三角形(图1-45)。

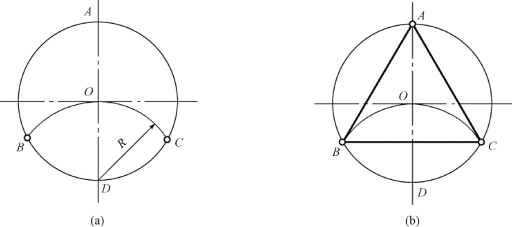
图1-45　用圆规和三角板作圆的内接正三角形

(a)以点D 为圆心，R 为半径作弧得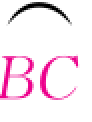;(b)连接AB、BC、CA 即得圆的内接正三角形

2)用丁字尺和三角板作圆的内接正三角形(图1-46)。

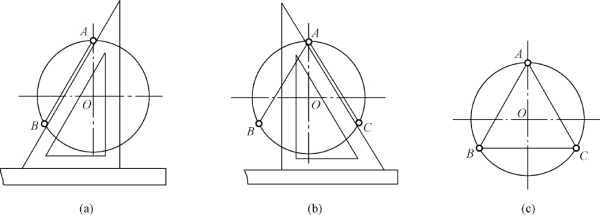
图1-46　用丁字尺和三角板作圆的内接正三角形

(a)将30°三角板的短直角边紧靠丁字尺工作边，沿斜边过点A 作AB;(b)翻转三角板，沿斜边过点A 作AC;(c)连接BC 即得圆的内接正三角形

(2)正四边形(图1-47)。

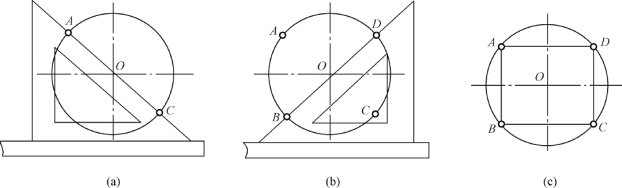
图1-47　用丁字尺和三角板作圆的内接正四边形

(a)将45°三角板的直角边紧靠丁字尺工作边，过圆心O 沿斜边作直径AC;(b)翻转三角板，过圆心O 沿斜边作直径BD;(c)依次连接AB、BC、CD、DA，即得圆的内接正四边形(www.xing528.com)

(3)正五边形(图1-48)。

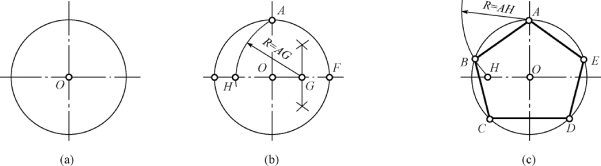
图1-48　作圆的内接正五边形

(a)已知圆O;(b)作出半径OF 的等分点G，以点G 为圆心、GA 为半径作圆弧，交直径于点H;(c)以AH 为半径，分圆周为五等份，依次连各等分点A、B、C、D、E，即所求

(4)正六边形(图1-49)。

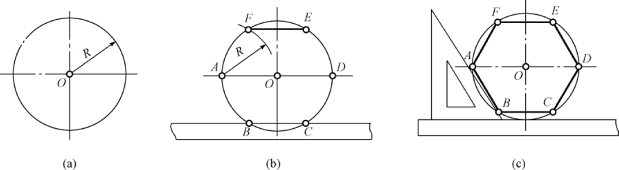
图1-49　作圆的内接正六边形

(a)已知半径为R 的圆;(b)用R 划分圆周为六等份;(c)依次连接各等分点A、B、C、D、E、F，即所求

(5)任意正多边形。以圆内接正七边形为例，说明任意正多边形的画法，如图1-50所示。

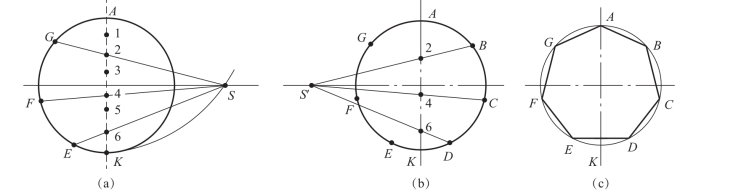
图1-50　圆内接正七边形

(a)将直径AK 等分为七等份，以点A 为圆心、AK 为半径作弧，交水平中心线于点S;(b)延长连线S2、S4、S6，与圆周交得点G、F、E，再用边长AG 作出它们的对称点B、C、D;(c)依次连接各等分点A、B、C、D、E、F、G，即可得到圆内接正七边形