铸造充型过程的数值模拟优化

液态金属或合金的充型过程是铸造成形的第一个阶段，也是对铸件的成形质量具有较大影响的一个阶段，浇注系统设计得合理与否将对铸件的质量产生影响。充型及浇注过程中产生的具体缺陷有：浇不足、冷隔、冲砂、粘砂、包砂、起皮和夹渣等。因而通过铸造流动与充型过程数值模拟来观察和研究浇注系统设计的合理性，以及研究流动与充型对铸件质量的影响具有十分重要的意义。铸造流动与充型过程数值模拟也为初始温度场的处理提供了更为合理的方法。

1.充型过程的数学及流体力学基础

通常情况下气体和液体被称为流体，严格意义上讲，流体是一种在微小剪应力作用下会发生连续变形的物质。其充型阶段的流动属于带有自由表面黏性不可压缩非稳态流动，包含着动量传递、质量传递和能量传递，要完整地描述其流动、充型和传热状态和过程，其控制方程需要符合动量守恒、质量守恒和能量守恒定律。型腔充填过程中流动现象的数值模拟，首先是求解这一非稳态过程中流体流动的控制方程组，也就是Navier⁃Stokes方程、连续方程及能量方程，以此建立模拟计算的数理模型。

1）流体的性质包括压缩性与热胀性、黏性，流体还可以分为理想流体、牛顿流体和非牛顿流体。

流体的压缩性与热胀性是指流体在压缩和受热时会分别产生体积缩小和体积增大的特征。流体的黏性是指当流体的流层之间出现相对位移时，不同流动速度的流层之间所出现的切向黏性力，可由牛顿黏性定律来表述：

式中 τ_yx——切应力，其中第一个下标y表示切应力的法线方向，第二个下标x表示切应力的方向；

η——常数，表示流层间出现相对流速时的内摩擦特性，称为流体的动力黏度系数。

将流体的动力黏度系数η除以流体的密度，则得到流体的运动黏度系数ν。理想流体是Pascal在1663年提出的概念，是指内部无摩擦力、无黏性的流体，既不能承受拉力也不能承受切力，只能传递压力，只能在压力下流动，是不可压缩的。牛顿流体是指在流动时，黏性力与速度之间的关系符合牛顿黏性定律的流体。其他在流动过程中黏性力与速度之间的关系不符合牛顿黏性定律的流体称为非牛顿流体。

2）黏性流体流动的基本方程包括连续性方程、动量守恒方程和能量守恒方程。连续性方程实质上体现了流动过程中的质量守恒，既适合于理想流体，又适合于黏性流体，其表达式为

式中 τ_yx——切应力，其中第一个下标y表示切应力的法线方向，第二个下标x表示切应力的方向；

η——常数，表示流层间出现相对流速时的内摩擦特性，称为流体的动力黏度系数。

将流体的动力黏度系数η除以流体的密度，则得到流体的运动黏度系数ν。理想流体是Pascal在1663年提出的概念，是指内部无摩擦力、无黏性的流体，既不能承受拉力也不能承受切力，只能传递压力，只能在压力下流动，是不可压缩的。牛顿流体是指在流动时，黏性力与速度之间的关系符合牛顿黏性定律的流体。其他在流动过程中黏性力与速度之间的关系不符合牛顿黏性定律的流体称为非牛顿流体。

2）黏性流体流动的基本方程包括连续性方程、动量守恒方程和能量守恒方程。连续性方程实质上体现了流动过程中的质量守恒，既适合于理想流体，又适合于黏性流体，其表达式为

式中 u、v、w——速度在三个轴向上的分量；

ρ——流体的密度。

式中 u、v、w——速度在三个轴向上的分量；

ρ——流体的密度。

对于不可压缩的流体，其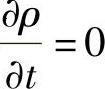，则（10⁃46）式可变化为

对于不可压缩的流体，其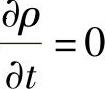，则（10⁃46）式可变化为

式（10⁃47）就是铸造过程模拟中通常使用的连续性方程。

动量守恒方程体现了流体在流动过程中的动量守恒，可以用Navier⁃Stokes方程来描述。这里将充型过程中的液态金属视为三维非稳态、不可压缩牛顿流体，则有：

式（10⁃47）就是铸造过程模拟中通常使用的连续性方程。

动量守恒方程体现了流体在流动过程中的动量守恒，可以用Navier⁃Stokes方程来描述。这里将充型过程中的液态金属视为三维非稳态、不可压缩牛顿流体，则有：

式中 u、v、w——速度向量在x、y、z方向上的分量；

p——压力；

t——时间；

ρ——流体密度；

ν——运动黏度；

g_x、g_y、g_z——重力加速度在x、y、z方向上的分量，实际上g_x和g_y均为0；

▽²——拉普拉斯算子。

能量守恒方程反映了在浇注过程中流体与铸型热交换的规律，体现了充型和凝固过程中的能量守恒，当流体不可压缩时，在直角坐标系下方程的表达式为

式中 u、v、w——速度向量在x、y、z方向上的分量；

p——压力；

t——时间；

ρ——流体密度；

ν——运动黏度；

g_x、g_y、g_z——重力加速度在x、y、z方向上的分量，实际上g_x和g_y均为0；

▽²——拉普拉斯算子。

能量守恒方程反映了在浇注过程中流体与铸型热交换的规律，体现了充型和凝固过程中的能量守恒，当流体不可压缩时，在直角坐标系下方程的表达式为(www.xing528.com)

式中 c——流体的比热容；

ρ——流体密度。

能量守恒方程和动量守恒方程一般可以分别求解，即先求出速度和压力分布，然后再利用能量守恒方程求出温度分布。

3）初始条件和边界条件与温度场一样，流场的求解也需要定解条件。流场的定解条件也是初始条件和边界条件，只有在给定上述两个条件的情况下，才能使流场具有唯一解。

初始条件是求解非定常流动时的必要条件，需要给出初始时刻的速度分布和温度分布。铸件的充型过程是非定常流动，因此需要给定初始条件才能进行金属液流动速度场和压力场的求解过程。如果是求解流场时耦合温度场计算，则还要给出初始的温度场分布。

边界条件是指流体在运动的边界上运动参数应该满足的条件，包括固壁界面条件、液⁃液及液⁃气界面条件。

固壁界面条件包括多种情况，无滑移条件是指当黏性流体流过不动的固体壁面时，其法向速度应当等于零，并且切向速度也等于零，这种情况也属于无黏附条件。

当固体壁面在流体中运动时，黏附于固体壁面的流体质点的速度等于固体壁面的速度。

当固体壁面是多孔介质时，有流体穿过壁面，则切向速度为零，而法向速度等于流体穿过壁面的速度。

温度边界条件是需要给出固体壁面上的温度，通常认为与固体壁面接触的流体质点与固体壁面上的温度相同。

对于液⁃液及液⁃气界面，如果两种介质交界面互不渗透，而且又不发生分离的连续性条件，则在交界面处的法向速度相等。对于黏性流体的两种介质交界面处，切向速度和温度也应该相等，而在理想流体中交界面处切向速度和温度可以不等。

在自由表面处的边界条件，自由表面是液⁃气两相介质的交界面，其动力学边界为：如果气体介质具有常值压力p₀，则应力向量的法向和切向分量符合：p_nn=-p₀，p_nt=0。

2.铸件充型数值模拟方法

铸件充型数值模拟方法主要是采用有限差分法或有限单元法来求解质量守恒方程、连续性方程、动量守恒方程，以获得流场的解。上述方程均为非线性偏微分方程，求解过程比较复杂，问题主要有两个方面：一方面是液态金属流动过程中存在着自由表面，需要确定自由表面的位置和形状；另一个方面是压力场的求解，目前尚无可以使用的明显方程，实际求解过程也比较费时，为此需要研究人员在流体力学、数学、计算机科学等学科和领域进行综合处理，在模型和算法等方面进行改进和提高。

1）自由表面的处理在目前主要有两个方法：MAC方法和VOF方法。MAC方法即标志网格法（Mark and Cell），也称为示踪粒子法，属于有限差分法中的原始变量法，是1965年美国LosAlamos国家实验室的Harlow和Welch提出的。在Euler矩形网格上建立了Navier⁃Stokes方程的差分格式，在网格的格子中设标志点，标志点不具有质量，于初始时刻设置在有流体的格子中，以后在流场中随流体运动，用来跟踪自由表面的粒子。流体的运动是通过用一个个标志点的移动来实现的。在单向流问题中，标志点不参与力学量的计算过程，只表明自由表面的位置、形状和流体运动的过程。在多向流问题中，标志点参与力学量的计算，同时还给出不同介质的界面位置。在显式或图形输出时，把标志点集合体的边缘视为自由表面，求解流体的基础方程时，距标志点群边缘最近的网格或单元边界视为自由表面。该方法的一个突出优点是能够生动地描述带有自由表面的液流的流态演化过程，不受单元形状的限制，能圆滑地表示自由表面，并可同时显式流体内部的流态，可以处理任意变形问题。

VOF方法即体积函数法（Volume of Fluid），同样是由美国Los Alamos国家实验室的研究人员提出的。首先需要定义一个流体体积函数F，当F=1时，表示满网格，网格处于流体域内；当F=0时，为空网格，表示网格内没有流体；当0＜F＜1时，表示网格内有流体，但没有充满，是边界网格。自由表面的位置是通过求解液相体积分数的传输方程来确定的，即

式中 c——流体的比热容；

ρ——流体密度。

能量守恒方程和动量守恒方程一般可以分别求解，即先求出速度和压力分布，然后再利用能量守恒方程求出温度分布。

3）初始条件和边界条件与温度场一样，流场的求解也需要定解条件。流场的定解条件也是初始条件和边界条件，只有在给定上述两个条件的情况下，才能使流场具有唯一解。

初始条件是求解非定常流动时的必要条件，需要给出初始时刻的速度分布和温度分布。铸件的充型过程是非定常流动，因此需要给定初始条件才能进行金属液流动速度场和压力场的求解过程。如果是求解流场时耦合温度场计算，则还要给出初始的温度场分布。

边界条件是指流体在运动的边界上运动参数应该满足的条件，包括固壁界面条件、液⁃液及液⁃气界面条件。

固壁界面条件包括多种情况，无滑移条件是指当黏性流体流过不动的固体壁面时，其法向速度应当等于零，并且切向速度也等于零，这种情况也属于无黏附条件。

当固体壁面在流体中运动时，黏附于固体壁面的流体质点的速度等于固体壁面的速度。

当固体壁面是多孔介质时，有流体穿过壁面，则切向速度为零，而法向速度等于流体穿过壁面的速度。

温度边界条件是需要给出固体壁面上的温度，通常认为与固体壁面接触的流体质点与固体壁面上的温度相同。

对于液⁃液及液⁃气界面，如果两种介质交界面互不渗透，而且又不发生分离的连续性条件，则在交界面处的法向速度相等。对于黏性流体的两种介质交界面处，切向速度和温度也应该相等，而在理想流体中交界面处切向速度和温度可以不等。

在自由表面处的边界条件，自由表面是液⁃气两相介质的交界面，其动力学边界为：如果气体介质具有常值压力p₀，则应力向量的法向和切向分量符合：p_nn=-p₀，p_nt=0。

2.铸件充型数值模拟方法

铸件充型数值模拟方法主要是采用有限差分法或有限单元法来求解质量守恒方程、连续性方程、动量守恒方程，以获得流场的解。上述方程均为非线性偏微分方程，求解过程比较复杂，问题主要有两个方面：一方面是液态金属流动过程中存在着自由表面，需要确定自由表面的位置和形状；另一个方面是压力场的求解，目前尚无可以使用的明显方程，实际求解过程也比较费时，为此需要研究人员在流体力学、数学、计算机科学等学科和领域进行综合处理，在模型和算法等方面进行改进和提高。

1）自由表面的处理在目前主要有两个方法：MAC方法和VOF方法。MAC方法即标志网格法（Mark and Cell），也称为示踪粒子法，属于有限差分法中的原始变量法，是1965年美国LosAlamos国家实验室的Harlow和Welch提出的。在Euler矩形网格上建立了Navier⁃Stokes方程的差分格式，在网格的格子中设标志点，标志点不具有质量，于初始时刻设置在有流体的格子中，以后在流场中随流体运动，用来跟踪自由表面的粒子。流体的运动是通过用一个个标志点的移动来实现的。在单向流问题中，标志点不参与力学量的计算过程，只表明自由表面的位置、形状和流体运动的过程。在多向流问题中，标志点参与力学量的计算，同时还给出不同介质的界面位置。在显式或图形输出时，把标志点集合体的边缘视为自由表面，求解流体的基础方程时，距标志点群边缘最近的网格或单元边界视为自由表面。该方法的一个突出优点是能够生动地描述带有自由表面的液流的流态演化过程，不受单元形状的限制，能圆滑地表示自由表面，并可同时显式流体内部的流态，可以处理任意变形问题。

VOF方法即体积函数法（Volume of Fluid），同样是由美国Los Alamos国家实验室的研究人员提出的。首先需要定义一个流体体积函数F，当F=1时，表示满网格，网格处于流体域内；当F=0时，为空网格，表示网格内没有流体；当0＜F＜1时，表示网格内有流体，但没有充满，是边界网格。自由表面的位置是通过求解液相体积分数的传输方程来确定的，即

通过求解每个单元中的液相体积分数，就可确定自由表面的位置和形状。VOF法的优点是减少了自由表面计算的工作量，由于VOF法追踪的是网格中的流体体积，而非跟踪自由表面流体质点的运动（如MAC法、SMAC法和边界元法），因此可以处理自由面重入等非线性现象。其缺点是比较难用于非正交网格，当单元尺寸大时，自由表面形状精度低，式（10⁃53）在离散格式上容易造成很大的假扩散问题，致使计算结果出现所谓的界面模糊现象，即在某一方向上充满单元（F=1）与空单元（F=0）之间存在大量的自由表面单元（0＜F＜1），这种自由表面单元越多，界面模糊现象越严重。

2）压力场的处理可采用SIMPLE方法，该方法是求解压力连续方程的半隐式方法，是计算非定域、不稳定速度场的一种分离式求解方法。分离式解法的关键是如何求解压力场，或者在假定了压力场后如何改进它。实际计算中主要是通过迭代法进行求解，特点是压力场和速度场同时迭代。

由于求解压力场极为耗时，计算量相当大，因而在实际应用中研究人员在压力场⁃速度场的迭代方法上，在稀疏矩阵方程组的求解方面进行有效的改进，如基于SIMPLE方法的SIMPLER方法。SIMPLEC法是SIMPLE法的改进，它与SIMPLE法的区别在于速度校正公式的不同，目的是提高计算的收敛性。CG法（Conjugate Gradient Methods）也称为共轭梯度法，在迭代求解大型稀疏矩阵方程组时具有很好的收敛性。SCGS法是对单元中的速度变量采用同样的处理方式，避免了SIMPLE法中的近似压力场和压力修正方程，提高了计算速度。API法（Adaptive Pressure Iteration）是在原有的SOLA法的基础上提出的一种压力修正方法，在SOLA法迭代减慢时，用较为准确的压力猜测值可以加快迭代收敛的速度。

通过求解每个单元中的液相体积分数，就可确定自由表面的位置和形状。VOF法的优点是减少了自由表面计算的工作量，由于VOF法追踪的是网格中的流体体积，而非跟踪自由表面流体质点的运动（如MAC法、SMAC法和边界元法），因此可以处理自由面重入等非线性现象。其缺点是比较难用于非正交网格，当单元尺寸大时，自由表面形状精度低，式（10⁃53）在离散格式上容易造成很大的假扩散问题，致使计算结果出现所谓的界面模糊现象，即在某一方向上充满单元（F=1）与空单元（F=0）之间存在大量的自由表面单元（0＜F＜1），这种自由表面单元越多，界面模糊现象越严重。

2）压力场的处理可采用SIMPLE方法，该方法是求解压力连续方程的半隐式方法，是计算非定域、不稳定速度场的一种分离式求解方法。分离式解法的关键是如何求解压力场，或者在假定了压力场后如何改进它。实际计算中主要是通过迭代法进行求解，特点是压力场和速度场同时迭代。

由于求解压力场极为耗时，计算量相当大，因而在实际应用中研究人员在压力场⁃速度场的迭代方法上，在稀疏矩阵方程组的求解方面进行有效的改进，如基于SIMPLE方法的SIMPLER方法。SIMPLEC法是SIMPLE法的改进，它与SIMPLE法的区别在于速度校正公式的不同，目的是提高计算的收敛性。CG法（Conjugate Gradient Methods）也称为共轭梯度法，在迭代求解大型稀疏矩阵方程组时具有很好的收敛性。SCGS法是对单元中的速度变量采用同样的处理方式，避免了SIMPLE法中的近似压力场和压力修正方程，提高了计算速度。API法（Adaptive Pressure Iteration）是在原有的SOLA法的基础上提出的一种压力修正方法，在SOLA法迭代减慢时，用较为准确的压力猜测值可以加快迭代收敛的速度。