温度场的数值模拟是以傅里叶(Fourier)导热微分方程为基础,采用数值计算的方法进行求解的。
1.凝固过程的传热学基础
凝固过程的传热可分为三种方式:传导传热、对流传热和辐射传热。导热分析的研究最终归结为求解傅里叶方程,其数学表达式如下:
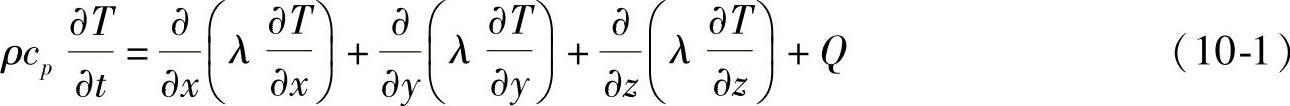
式中 ρ——密度(g/cm3);
cp——比定压热容[J/(kg·K)];
T——温度(K);
t——时间(s);
λ——热导率[W/(m·K)];
x、y、z——坐标(m);
Q——内热源,按下式计算:

式中 L——熔化潜热(J/kg);
fS——固相率。
根据导热微分方程式(10⁃1)可进行传热解析。导热微分方程式(10⁃1)的求解主要有两种方法:解析法和非解析法。
解析法是以假定和近似处理为前提,通过误差函数进行求解的。该方法在方程的求解过程中会受到很多限制,即使是一维传热,在一系列的假定处理后,计算会变得复杂,至于形状很复杂的铸件基本上无法计算。但是,解析法毕竟是将温度或凝固层厚度作为时间的函数形式给出的,能够较清晰地揭示凝固过程的规律,仍有研究的理论价值。
非解析法包括:图解法、电模拟法和数值模拟法。借助于计算机,数值模拟法得以迅速发展,目前成为非解析计算的主要算法,几乎完全代替其他的非解析法。
2.数值模拟计算方法
常用的温度场数值计算方法有三种:有限单元法(FEM)、边界元法(BEM)和有限差分法(FDM),其中有限差分法是三种方法中最常用的方法。
(1)有限单元法 有限单元法是一种近似计算方法,是由古典的变分计算演变而来的。最初用于求解弹性力学问题,20世纪50年代中期用于工程结构,目前广泛应用于铸件凝固的温度场、应力场计算。
有限单元法求解温度场的具体过程包括:
1)铸件实体的离散化,即将铸件的几何体离散,或者称为剖分,形成由单元体组成的体系。单元体的形状就三维体系而言,可以是四面体或者是六面体;就二维体系而言可以是三角形或者是四边形。离散后单元与单元之间由单元的节点相互连接起来,连接后铸件就变成了由大量单元体以一定的方式连接而成的离散几何体,因而有限元分析计算所获得的结果是近似的。
2)单元体的变分是依据变分原理进行的,变分后形成单元体特性数据矩阵。
3)单元体的总体合成利用边界条件和初始条件把各个单元体按原来的结构重新连接起来,形成整体线性方程组,从而得到整体的特性矩阵和特性阵列。
4)求解未知场的具体量值是根据方程组的特点以特定的计算方法进行,通过计算解出未知场的具体量值。
有限单元法求解温度场具有如下特点:
1)离散的任意性。如图10⁃1所示,在三维系统中采用四面体,在二维系统中采用三角形单元,系统的边界或界面处可获得比有限差分法更接近实际铸件表面的界面或边界,单元的划分具有任意性,可根据精度的需要,温度的变化幅度来剖分单元,确定单元的大小。对于界面或边界处,可根据界面的曲率变化来剖分,确定具体的单元及其大小。
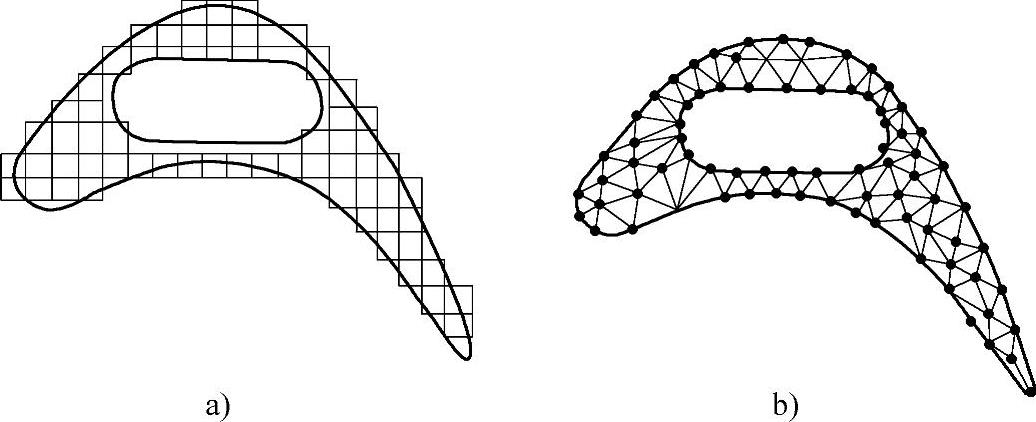
图10⁃1 有限单元法与有限差分法的单元剖分对比
a)有限差分法的单元剖分 b)有限单元法的单元剖分
2)可便利地实现温度场与应力场的偶合计算。有限元法起源于力学计算,对于应力场的计算可以便捷地进行,因而可以用有限元法进行上述两场的计算,实现该两场的偶合。对于有限差分法,只能进行温度场计算。由于算法的原因,该方法无法进行应力场的计算。这样在计算时,还需要由有限元法进行应力场计算,然后才能进行两场的偶合。
(2)边界元法 边界元法是由边界积分法发展起来的一种计算方法,在原理上与以往的计算方法不同。边界元法通过对区域的边界或界面进行离散,对控制方程施加拉格朗日变换,求出变换后的温度场,最后用拉格朗日逆变换求出原始温度场的数值解。
与前两种方法相比,边界元法的主要优点是将问题的维数降低,从而降低了内存的占用量。该方法的缺点是计算公式及过程比较复杂,计算时间较长,因而限制了人们的使用,目前人们很少使用该方法进行温度场计算及凝固模拟。
(3)有限差分法 有限差分法是目前最为广泛应用的数值计算方法,是将式(10⁃1)中的微分项用差分项代替,用有限个网格节点代替连续的求解域,推导出含有离散点上有限个未知的差分方程组,将微分方程问题转化为代数问题,最后求解差分方程组以获得微分方程的数值近似解。根据差分格式的不同,有限差分法可分为显式差分格式、隐式差分格式和交替方向隐式差分格式。此外又可划分为向前差分、向后差分和中心差分。
差分是微分的近似,两者的关系可由式(10⁃3)来描述。
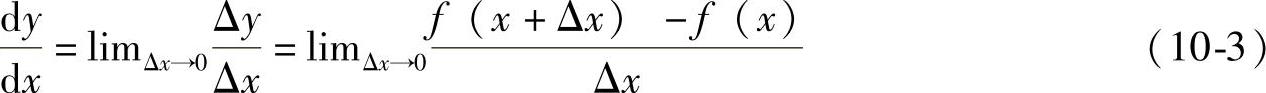
式中 dy、dx——函数及自变量的微分;
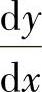 ——函数对自变量的导数,又称为微商;
——函数对自变量的导数,又称为微商;
Δy、Δx——函数及自变量的差分;
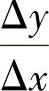 ——函数对自变量的差商。
——函数对自变量的差商。
对于一阶导数,三种差分的相互关系如图10⁃2所示,计算公式如下:
向前差分为
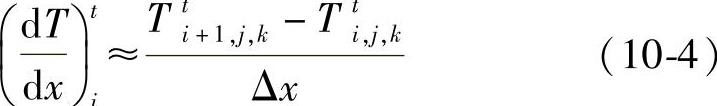
向后差分为
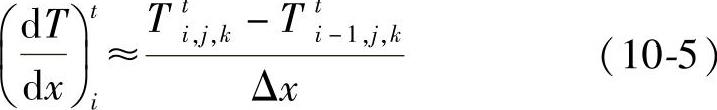
中心差分为
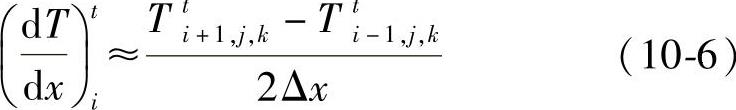
温度对时间的向前差分为
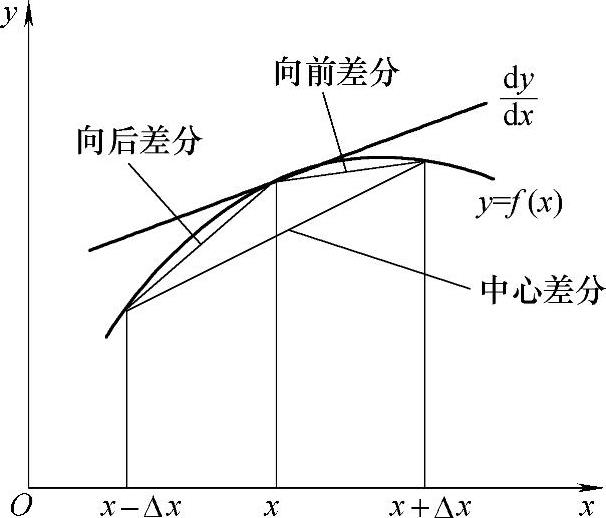
图10⁃2 几种差分与微分

对于二阶导数,可以进行推导,推导后得向后差分公式如下:
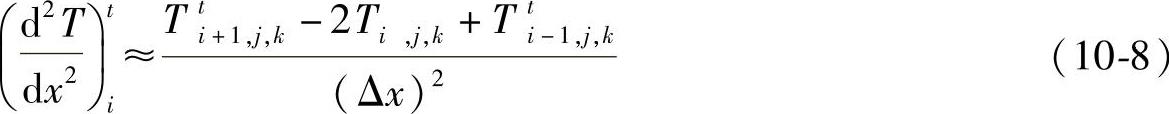
差分代替微分后,式(10⁃1)转化为以下向前差分式:
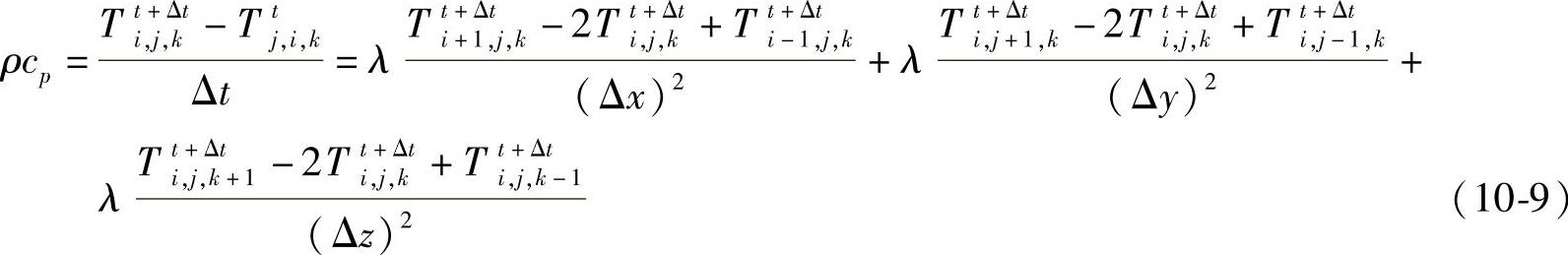
式(10⁃4)~式(10⁃9)中,单元体及对应的坐标体系如图10⁃3所示。
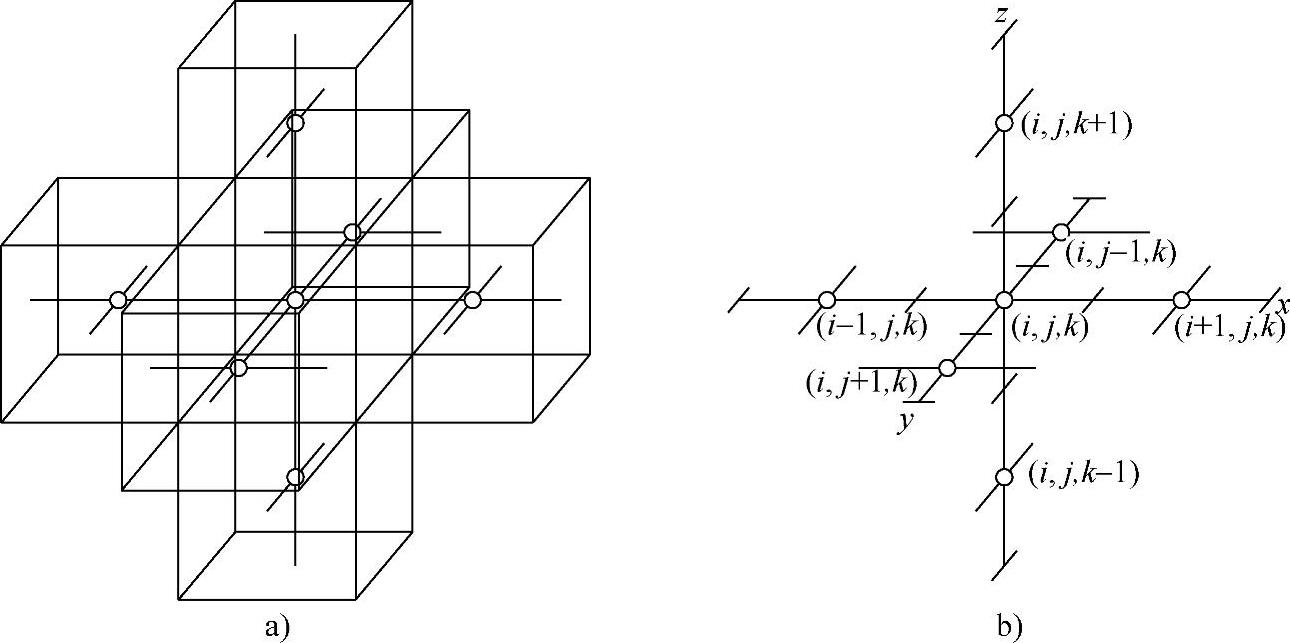
图10⁃3 三维系统中单元与坐标及节点
a)单元及节点 b)对应坐标轴上的节点
3.凝固潜热的处理
金属及合金在凝固过程中,潜热的释放使传热的性质发生改变,增加了凝固传热的复杂性,这也是金属凝固与一般传热过程的区别所在。对于凝固过程前热的处理,可将其视为具有内热源的导热问题。潜热的处理方法包括:温度回升法、等效比热法和热焓法,其中前两种是常用的潜热处理方法。
(1)温度回升法 将金属凝固时释放的潜热折算成同等热量所产生的温度回升,并逐步补偿或释放到相应的单元中,使按常规冷却的单元因获得温度补偿而保持在相变温度,直到潜热释放完毕。温度补偿处理过程的冷却曲线如图10⁃4所示。
该方法适用于纯金属、共晶合金或者凝固范围很窄的合金。具体计算过程为:当单元的温度降到熔点TS时,假定单元e的体积为ΔVe,所释放的潜热为
ΔQe=ρLΔVe (10⁃10)
折算成等值传热所降温度为ΔTe,则
ΔTe=ΔQe/(ρcΔVe)=L/c (10⁃11)
根据温度回升法有
ΔTe=ΔT1+ΔT2+…+ΔTn (10⁃12)
式(10⁃12)中,ΔT1为时间步长Δt1内的单元“1”在常规冷却时产生的温度下降。当最后一个时间步长Δtn的回升温度折算后,潜热即处理完毕。
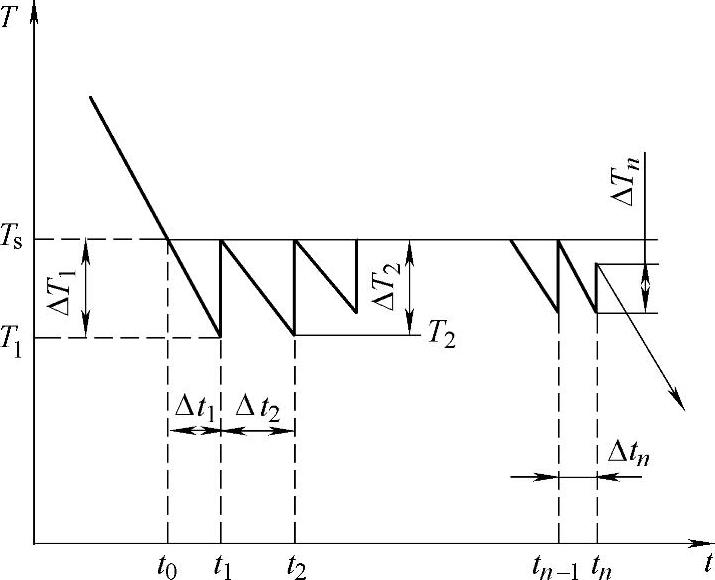
图10⁃4 温度补偿处理过程的冷却曲线
(2)等效比热法 将结晶潜热折算成比热容叠加到合金的实际比热容中,叠加后的比热容作为合金结晶温度区间的修正值比热容,即把结晶区间的比热容与结晶潜热综合考虑成一种比热容,即等效比热容,以此处理结晶温度区间的凝固。
等效比热法适用于具有凝固温度区间的合金,将其定义为ce,单元i在结晶温度区间内,单位体积、单位时间内固相率的增加率为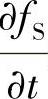 对应潜热释放量为
对应潜热释放量为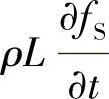 ,考虑潜热释放的导热微分方程为
,考虑潜热释放的导热微分方程为
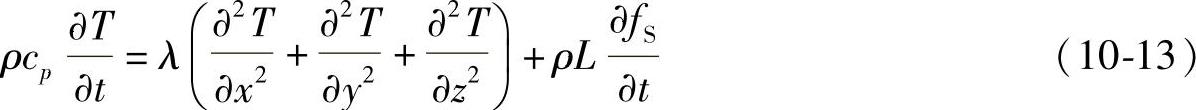
而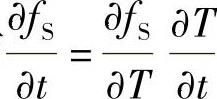 ,并令
,并令
 (https://www.xing528.com)
(https://www.xing528.com)
则(10⁃13)式可以整理转换为
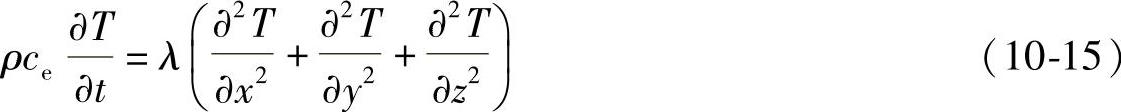
式(10⁃15)中的ce可由式(10⁃14)确定,由该式可见,关键是求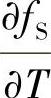 。而
。而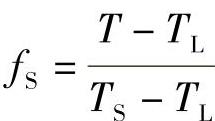 ,因此,
,因此,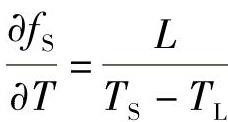 ,所以有:
,所以有:

式中 TL——液相线温度。
(3)热焓法 热焓法主要是通过热焓变换来处理式(10⁃1)。当考虑凝固相变时,合金的热焓为
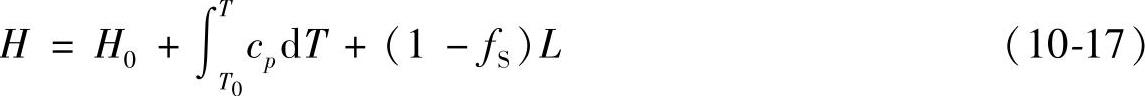
式中 H——热焓;
T0——基准温度;
H0——基准温度时的热焓。
由式(10⁃17)对温度求导可得
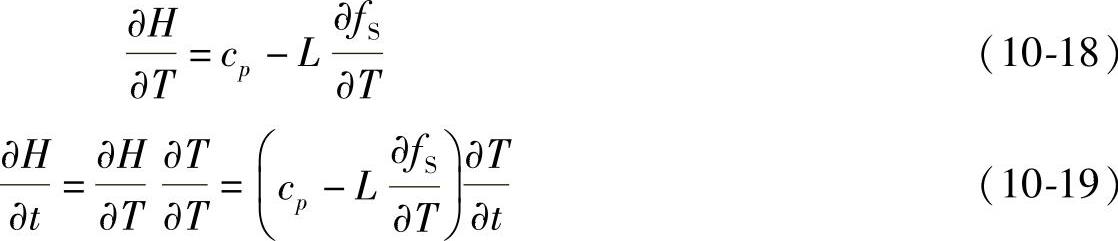
经上述变换后,傅里叶方程式可变为
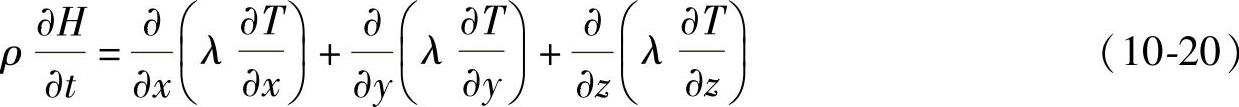
当采用显式差分格式对上式进行离散后,可以直接求出下一时刻的热焓值,然后根据式(10⁃17)可以求出下一时刻所对应的温度值。
假设合金的cp为常数,结晶潜热在凝固区间均匀释放,合金的固相率与温度呈线性关系:

则可得
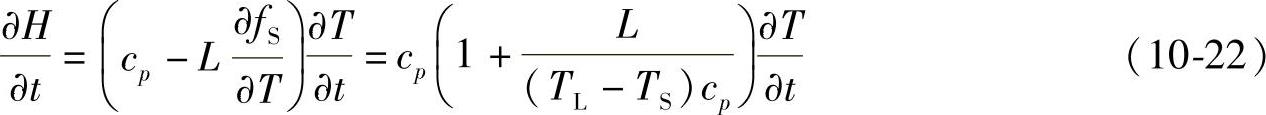
对上式进行离散后可直接由下一时刻的热焓值来计算所对应的温度值。
采用热焓法处理结晶潜热时,可适用于纯金属和共晶合金,也适用于具有凝固温度区间的合金。对于具有固定熔点Tm的纯金属或共晶合金,其热焓表达式如下:
当T<Tm时为

当T=Tm时为

当T>Tm时为
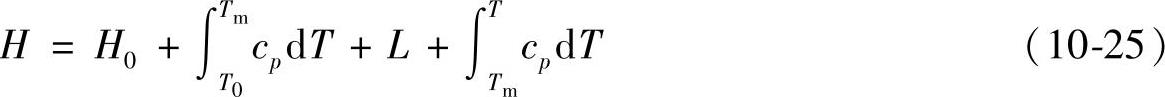
4.导热方程的定解条件
特定温度场的描述需要确定凝固过程的具体条件,只有当具体条件表征充分时,导热微分方程才能有定解。上述条件也称为导热方程的定解条件,包括两个方面,即初始条件和边界条件。
(1)初始条件 初始条件是指所计算体系在时间为0时刻的温度分布。根据对初始条件的简化和处理方法的不同可以分为下面几种方法。
最简单的初始条件处理方法是假定铸型的初始温度为常数,即室温。铸件内部的初始温度为浇注温度。铸件⁃铸型界面处的初始温度则采用特殊方法进行处理,主要有:实测法、解析法、逼近法等几种方法。
为了避免对充型过程中强制对流和凝固过程中高温液体金属自然对流的模拟计算,初始温度场经常是从浇注结束后某一时刻开始,取该时刻的铸件铸型温度场作为初始条件,该方法适用于快浇大中型铸件的砂型铸造。
目前比较理想的初始条件处理方法是流动传热偶合模拟计算法,该方法考虑了流动对温度场的影响,实现了边浇边凝这一过程的处理,是目前最接近实际凝固的处理方法。
(2)边界条件 边界条件按传热学的分类方法可分为三类,即第一类边界条件、第二类边界条件和第三类边界条件。
1)第一类边界条件也称为Dirichlet边界,是指给定了传热系统边界上各点的温度值的边界。边界温度Tw的表达式为
Tw=f(s,t) (10⁃26)
式中 s——位置参量,也可以表示为x、y、z;
t——时间。
也就是说,边界温度Tw是位置s和时间t的函数。对于非稳态导热问题,该类边界条件也可以是给定温度为传热系统边界上空间位置与时间的函数。该类边界条件中最简单的形式就是给定边界温度保持不变,即Tw=常数。
2)第二类边界条件也称为Neumann边界,是指给出传热系统边界上各点的沿边界法向量的热流密度。

对于非稳态导热问题,该类边界条件也可以是给定热流密度为边界上空间位置与时间的函数。该类边界条件中最简单的形式是给定边界上的热流密度保持定值,即qw=常数,应用较为广泛的是绝热边界条件,此时qw=0。
3)第三类边界条件称也为Robin边界,给出传热系统边界上各点处沿法线方向的热流密度与边界温度的线性关系。

式中 h——边界上的换热系数;
Tw——边界温度;
Tf——环境温度。
对于非稳态导热过程,h和Tf均可为时间的函数。
(3)实际边界情况 实际铸件凝固过程中的边界情况要复杂得多,大多不仅仅是上述三类边界条件中的一种,往往是多种边界条件的复合,具体情况包括:冒口上表面直接与空气、铸件与铸型、铸件+铸型与大气、冒口上表面+冒口覆盖剂与环境等边界。
1)对于上述第一种情况,即冒口上表面直接与空气换热,可认为是辐射散热,其换热边界条件可表示为

式中 ε——辐射体黑度,表明该物体接近黑体的程度;
σ——辐射系数常数。
实际应用时,常采用线性化处理进行简化,从而使该类边界条件具有与对流换热边界条件类似的形式,即

式中 hr——辐射换热系数,其计算公式为
hr=εσ(T2w+T2f)(Tw-Tf) (10⁃31)
对于瞬态导热问题,在采用式(10⁃30)计算辐射换热系数时,表面温度Tw可近似采用前一时刻的温度值进行近似,简化的同时会产生一定的误差。
实际导热处理时,物体表面经常同时存在着对流和辐射两种换热,这时边界条件为
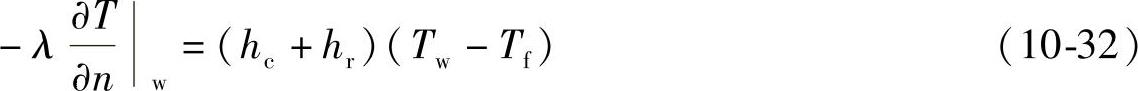
2)对于第二种情况,即铸件与铸型之间的换热,可分为紧密接触型界面和非紧密接触型界面。紧密接触型界面就是铸件与铸型之间紧密贴紧,不产生间隙。相互贴紧的两个表面具有相同的温度,在这种情况下,在某一温度下的热导率可按下式处理:

式中 λ1——铸件的热导率;
λ2——铸型的热导率。
实际上在绝大多数情况下,铸件与铸型的界面是非紧密接触型界面。该类界面在铸件与铸型之间存在一个气隙,因而铸件表面与铸型表面的温度是不同的。该类界面的热导率可按下式处理:

式中 R——气隙的热阻;
Δl——边界单元的两节点间的间距。
3)对于上述第三种情况,即铸件+铸型与大气之间的换热,在不同的铸造条件下处理方法也相对不同。当采用金属型铸造时,由于铸型的外表面温度较高,一般考虑铸型外表面与大气间发生自然对流和热辐射,系统的边界可按两种换热复合后的换热来处理。当采用砂型铸造时,铸型的外表面的温度相对较低,该界面的辐射换热可以忽略不计,只考虑自然对流换热。
5.材料的热物理性能数据
铸造相关材料包括铸件材料、铸型材料、冷铁材料、大气、保温冒口材料和保温补贴材料等。材料的热物理性能参数包括:热导率、比热容、密度和相应的界面换热系数等。热物理性能参数对模拟的精度具有较大的影响,材料的热物理性能数据又受温度等因素的影响。
材料的热物理性能参数一般均通过测试求得,由测试结果进行传热的反问题处理,也就是数学上的方程反演,处理后获得一系列与温度相对应的热物理性能参数。对于所得到的热物理性能参数往往需要经过数学处理方可使用。常用的方法有:常数法、线性或多项式拟合法、插值法等方法。常数法就是将温度处理成一个或者是几个区间,在每个区间内,材料的热物理性能参数被处理成常数;线性或多项式函数法就是采用回归或者拟合的方法把原始的热物理性能参数处理成线性的或者多项式数学函数,温度是自变量,热物理性能参数是温度的函数;插值法就是利用数学插值原理对每两点间的热物理性能参数进行插值计算,得到相应的热物理性能参数值。
凝固过程所涉及的材料很多,对此往往采用建立热物理性能参数数据库的方法来解决。可按材料的类别如钢、铜、铸铁等,或按材料的性质如金属材料、造型材料、保温材料进行分类存储和提取。
在凝固模拟计算中,往往需要先知道热物理性能参数然后求解温度场。当热物理性能参数为温度的函数时,又需要先确定温度再求解热物理性能参数。因此,实际模拟中常对热物理性能参数的求解做简化处理,如以上一时间步长计算的温度为参照计算出初步的热物理性能参数,以此初步的热物理性能参数计算本时间步长的温度场,再以此温度场计算本时间步长的热物理性能参数,以此热物理性能参数计算出的温度场即为本时间步长的最后温度场。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




