基于CMA的对抗样本生成方法探析

本方案主要用于黑盒图像识别模型环境下的靶向攻击问题，主要由三个算法组成，其中以 CMA 算法为主体算法，另外两个有效进化以及扰动压缩的算法为配合CMA 生成对抗样本所必需的算法。

在本方案设计的方法中，首先，利用有效进化算法找到一个有效种群；然后，利用 CMA 算法进化这个有效种群，直到找到局部最优解。此时，验证该局部最优解是否满足要求，即图像分类应该为目标类，且对抗样本与原始图像的L2 距离应该足够小。如果找到的局部最优解满足要求，就结束算法；否则，通过扰动压缩进一步优化找到的结果，直到找到的局部最优解满足要求。基于CMA 的高效黑盒对抗样本生成方法流程如图 4 − 3 − 1 所示。图中，SourceImage 为原始图像；TargetImage 为目标图像；ADVi 为第i 次迭代生成的对抗样本；TargetClass 为目标分类。

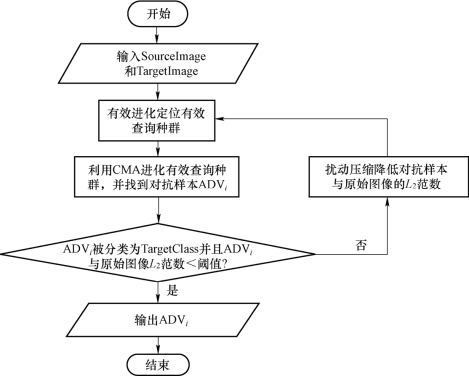
图4−3−1　基于CMA的高效黑盒对抗样本生成方法流程

参考白盒攻击C&W，将黑盒攻击的整个过程转化为一个优化问题，因此可以使用很多优化方法来解决该问题。在此使用最具有概率统计意义的优化方法——自适应协方差进化算法来优化该问题。

4.3.2.1 目标函数构建

由基础公式可知，这是一个条件优化问题，其优化条件为C(x+δ)=t，优化目标为求对抗样本与原始图像之间的最短距离，即最小化D(x,x+δ)。其中，x为原始图像；δ 为扰动噪声，t为目标分类。对此，可以类比拉格朗日乘数法的思想，将条件优化问题转化为无条件优化问题，即

由于C(x+δ)−t是一个不可微的量，在优化时不能提供有效的利好信息，因此应该按照目标函数含义来构造后半部分的公式内容。由于要求x+δ被分类为t的概率越高时，C(x+δ)−t越小，因此神经网络训练时的交叉熵函数就非常适合：

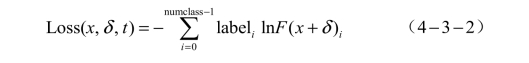
式中，labeli——one − hot表示法的标签表示法，即labeli=(0,0,0,…,0,1, 0,…,0)，只有第i位为1的长度为所有可能分类的数量的向量；

t——目标分类；

F(·)i ——分类器第i种分类的置信度输出。

Loss函数随着分类器对目标分类的置信度提高而减小，恰好符合本节对构造函数的要求。

对于靶向攻击而言，

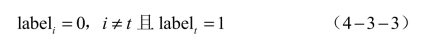
对于非靶向攻击而言，

因此，目标公式为

例如，

其中，

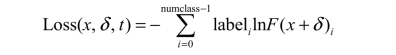
Loss函数可以表示输出与期望输出的差距，Loss函数值越小越好。

4.3.2.2 有效（Valid）进化

通常，使用高斯分布来代表一个不明的随机变量。所以在本节的研究中，假设对抗样本的扰动量δ在局部也是一种符合高斯分布的随机变量。

本节选取CMA作为攻击方法的主体算法。因为CMA是一种优秀的、基于统计学理论的进化算法。CMA的主要内容就在于进化种群的分布参数，即期望和标准差。CMA的进化对象正是假设的重要部分。本研究使用CMA 来进化扰动种群，并成功地生成了对抗样本。

有效样本是扰动量δ 在局部的特殊情况，因此推断有效样本也在局部符合特殊的高维高斯分布。基于该假设，利用 CMA 来定位有效样本。如果能利用这个假设完成对抗样本的生成任务，就可以验证这个假设。从实验结果的角度上说，该假设是正确的。具体验证过程见4.3.3 节。

在此，将目标公式作为适应度函数Fitness 的计算公式。由于使用的是进化算法，并且进化目标为目标函数最小化，所以直接使用目标公式作为Fitness 计算公式不仅方便并且准确，即

具体方法：当找到少量有效查询的样本时（如两个及以上），就可以通过少量有效样本来计算其均值与标准差，然后利用新的均值与标准差所对应的高斯分布重新生成采样。根据假设推理，新生成的采样中出现有效样本的概率更高，事实也确实如此。通过循环这个过程，能高效地定位有效样本所在的分布，并找到更多有效样本。有效进化过程示意如图 4 − 3 − 2所示。

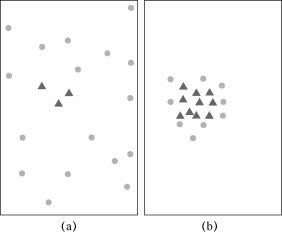
图4−3−2　有效进化过程示意

（a）一次随机采样结果；（b）通过有效定位操作后的采样结果

在图4 − 3 − 2 中，圆点或三角表示一次采样。其中，三角表示本次采样为有效样本，即目标分类在TopK中；圆点表示本次采样为无效样本。

将一个图像视为一个高维向量X(x1,x2,…,xn )，其可以表示为SourceImage+δ的形式，并认为δ～N(μ,σ)。其中，δ为原始样本与对抗样本之间的距离，即扰动；μ是向量δ的期望，也是一个高维向量μ(μ1,μ2,…,μn )；σ是向量X的标准差，也是一个高维向量σ(σ1,σ2,…,σn )。针对单像素而言，扰动概率分布函数为

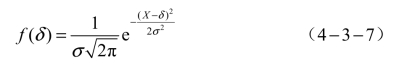
有效进化的进化公式为

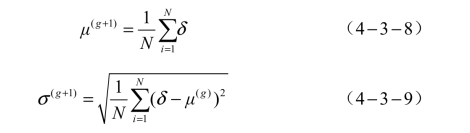
式中，,,,Xδσμ——单像素的位置、扰动、标准差、期望；

g——第g次迭代；

N——种群总数。

其中，采用的扰动为可以使原始图像成为有效查询的扰动。

此外，还有一个问题，即如何获取最初的少量有效查询？

目前已有的方案是直接通过在目标图像附近添加扰动的方式来获取初始的有效样本。但是，这种有效样本确定方式用于CMA有效进化上着实有些浪费。由于有效进化仅需少量的初始有效样本即可定位一大群有效样本，因此没有必要获得过多的初始有效样本。而且，所使用的主算法为CMA进化算法，初始有效样本提供的种群多样性越大，则对于后期进化越有好处。

综上所述，本方案提供一种对于后期进化更加有效率的初始有效查询获取方式。

所设计的方案需要输入原始图像以及目标图像，找到一幅原始图像与目标图像之间的图像，要求在这幅图像附近能很容易地找到少量有效样本，即(www.xing528.com)

搜索初始对抗样本x′

利用投影的方法，将目标图像逐渐投影到原始图像中，以寻找这幅中间图像，并将找到的这幅中间图像称为对抗攻击StartPoint。使用类似PGD的方法，通过限制StartPoint 像素取值的方式来完成投影。随着投影比例的加大，StartPoint 在高维空间越来越靠近目标分类的决策空间，其周围加入高斯扰动时能发现有效样本的概率更高。通过StartPoint 定位方法，可以很快地找到与原始图像L2 距离较小的有效样本群及其分布，相较于从目标图像直接出发，这省去了很多扰动压缩过程。这种方法称为靠近目标投影方法，其效果如图 4 − 3 − 3 所示。

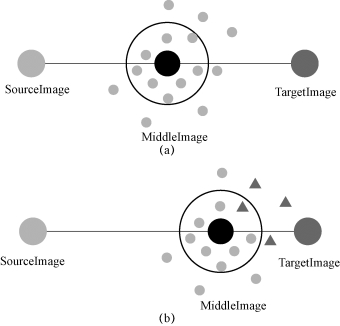
图4−3−3　靠近目标投影方法示意

（a）移动中间过程（未找到局部最优解）；（b）移动中间过程（找到局部最优解）

在图4 − 3 − 3 中，大圆点表示特殊图像，小圆点或三角表示一次采样，三角表示本次采样为有效样本，StartPoint 越向 TargetImage 靠近，在StartPoint 进行随机采样中找到有效样本的概率越高。

在实际的实验中，加入高斯扰动并不能使用标准的高斯分布 N（0,1）。这是由于通常将像素取值范围从[0,255]的离散值归一化为[0,1]的连续值。在图像领域，通常加N（0,0.001）的扰动，即扰动的范围约在0.2 个灰度以内，这是为了确保找到的扰动都是扰动幅度较小的扰动。

但是，扰动范围过小会导致以下两个问题：

（1）找到的种群多样性差。利用CMA 进化时，种群扩散缓慢（即σ 的进化缓慢），这导致CMA 算法整体进化缓慢。

（2）难以找到距离SourceImage 较近的StartPoint。特意使用靠近目标投影方法来定位 StartPoint，就是要找到尽可能离 SourceImage 近的、离TargetImage 远的初始有效样本。当采样越靠近TargetImage 时，采样为有效采样的概率就越高，但生成的采样离StartPoint 过于近，导致找到的初始有效样本是一些靠近（SourceImage, TargetImage）连线的样本，而那些与（SourceImage, TargetImage）向量正交的有效样本（StartPoint, Perturbation）将很难被发现，这与本方案的本意不符。所以，初始扰动标准差σ 是一个重要的超参数，在此采用自适应的方式（即扩散高斯扰动的方式）来确定对其选择。

扩散高斯扰动有助于找到尽量远离TargetImage 的有效样本，其示意如图 4 − 3 − 4 所示。

图 4 − 3 − 4（b）中 3 个圆圈的半径分别为高斯分布中σ 的 1 倍、2倍、3 倍，此处为表示采样高概率分布在采样中心的 3σ 范围以内。该图表示，如果StartPoint 与TargetImage 已经比较近，则利用扩散高斯扰动的方式即可找到初始有效样本，而不用进行目标图像靠近投影操作。通过这种方法，可以使找到 L2 距离尽量小且种群多样性尽量大的有效样本种群。

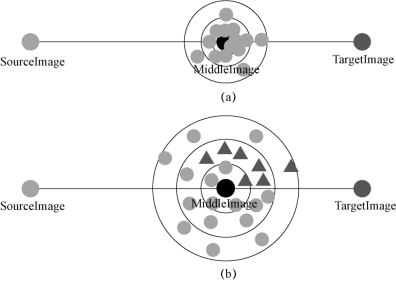
图4−3−4　扩散高斯扰动示意（书后附彩插）

（a）未找到解空间；（b）找到解空间

综上所述，在选择StartPoint 及初始扰动标准差σ 时，应该使StartPoint尽量靠近SourceImage，同时使初始扰动标准差σ 尽量大，这样就能找到多样性好且L2 距离小的有效样本种群，以便后续的攻击。

本方案提出使用扩散高斯扰动的方法并结合靠近目标投影方法来解决这一问题。在获取一幅中间图像后，在其附近逐渐扩大高斯扰动模型的标准差σ ，如果扩大到一定限度后还找不到有效样本，就移动StartPoint，进而获得σ 较为合适的初始有效样本。

有效进化的具体实现流程如图 4 − 3 − 5 所示。图中，SourceImage 为原始图像；TargetImage 为目标图像；StartPoint 为初始对抗样本；k 为扰动比例参数；μ 为扰动中心；σ 为扰动标准差；δ 为原始样本和对抗样本之间的距离，即扰动；GδS 为有效样本集。确定一个StartPoint，要求能在这个 StartPoint 附近找到一定量的有效样本；否则，可以通过提高TargetImage 的比例来提高找到初始有效样本的概率。循环查找，直到找到少量的初始有效样本。在本方案中，将这个“少量的”设定为2 个。本方案认为2 个初始有效样本辅以CMA 进化就可以定位一群有效样本。

4.3.2.3 CMA 进化有效种群

课题组认为，对抗样本是扰动量δ 在局部的特殊情况，因此推断对抗样本也在局部符合特殊的高维高斯分布。基于该假设，利用 CMA 进化有效样本种群，进而生成对抗样本。

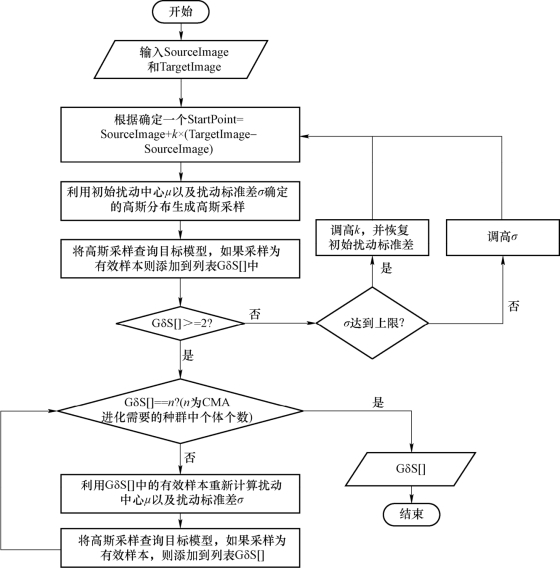
图4−3−5　有效进化流程示意

在每一轮迭代过程中，首先利用期望与标准差对应的高斯分布来生成种群，然后计算所有个体的适应度，接下来选取适应度较好的个体重新计算期望与标准差，直到找到了合乎要求的解；否则，循环迭代。

算法流程如图 4 − 3 − 5 所示。

进化公式为

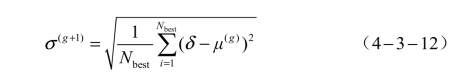
式中，Nbest ——所取的适应度较好扰动的数量。

利用 CMA 进化有效种群算法作为完成对抗样本生成工作的最外层的算法。每次迭代时，判断得到的进化结果能否满足攻击要求，若满足，则完成攻击结束迭代；否则，继续迭代。CMA 进化有效种群的算法流程示意如图4 − 3 − 6 所示。图中，μ 为扰动中心；σ 为扰动标准差；x 为原始图像；F 为目标分类器模型；t 为目标分类；r 为L2 距离扰动上界；a 为种群进化比例；n 为种群总体个数；GδS 为有效样本集；NowBestFitness为种群最佳个体适应度。

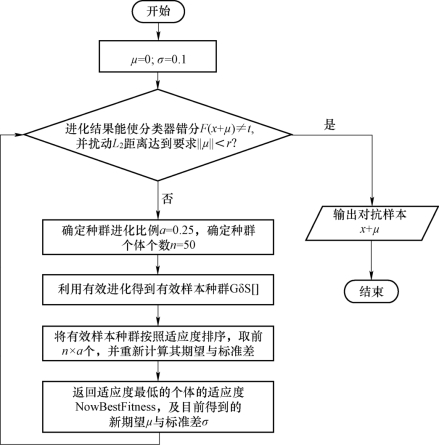
图4−3−6　CMA 进化有效种群的算法流程示意

4.3.2.4 扰动压缩

进化算法中有两个重要的参数决定了进化搜索的方向，一个是搜索广度，另一个是搜索深度。

CMA 是一个极其优秀的算法，它可以自适应地调整两个搜索方向的比例，当搜索到极值点附近时，它会自动收缩标准差，从而提高搜索深度、降低搜索广度。当搜索种群没有集中到某一点附近的趋势时，它会自动扩大标准差，从而提高搜索广度、降低搜索深度。

但是，由于高斯模型只拟合了局部对抗样本的概率模型，因此 CMA也十分容易陷入局部最优解。这一现象也可以验证本节的假设——对抗样本在局部符合一个高斯分布模型。因此，如果找到了L2 距离较小的有效样本，就可以找到L2 距离较小的对抗样本分布模型。为此，课题组尝试将扰动中心向原始图像靠拢，希望以此得到L2 距离较小的有效样本，从而达到跳出局部最优解的目的。实验证明，该方法确实可行。扰动压缩示意如图 4 − 3 − 7 所示。

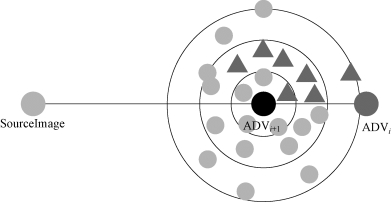
图4−3−7　扰动压缩示意（书后附彩插）

图4 − 3 − 7 表明，在得到一个局部最优解ADVi 后，将扰动中心向原始图像方向靠拢，如果找到了有效样本，就可以通过 CMA 算法找到新的较小的L2 距离下的对抗样本。

基于 CMA 的扰动压缩主要有两个问题需要解决：判断何时进行扰动压缩；如何进行自适应扰动压缩。

当CMA 进化有效种群达到局部最优解，且此时扰动分布产生的扰动使对抗样本被分类器高置信度分类为目标类时，就进行扰动压缩。因为此时CMA 已经无须再进化，扰动中心附近的扰动大部分都是可以使分类器错分的扰动，即已经找到了一个较好的局部最优解。所以，进行扰动压缩来跳出当前局部最优解。

但是，还存在一种情况：CMA 进化有效种群达到局部最优解，但扰动分布产生的扰动不能使对抗样本被分类器高置信度分类为目标类。这可能是因为 CMA 算法收敛过快，使得在进化时错过了好的局部最优解，所以通过提高扰动标准差并重新利用 CMA 进化该有效样本分布的方式来解决这一问题。判断扰动压缩何时进行的流程示意如图 4 − 3 − 8 所示。图中，LastBestFitness 为上一次迭代的种群最佳个体适应度；NowBestFitness为当前迭代的种群最佳个体适应度；Lastμ 为扰动压缩前的扰动中心；Lastσ 为扰动压缩前的扰动标准差；Convergence 为收敛阈值；CloseThreshold 为置信度阈值；σ 为扰动标准差。

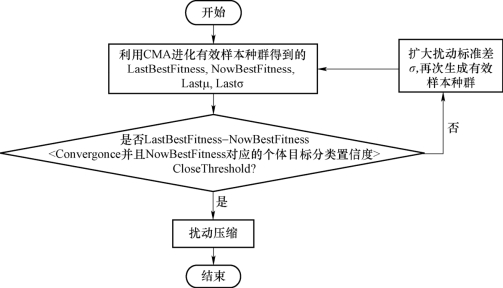
图4−3−8　判断扰动压缩何时进行的流程示意

在实验中，将固定扰动压缩后的扰动标准差（CDV）为某个值，课题组发现：当扰动压缩时的期望修改量（CEV）比3 × CDV 大时，扰动压缩的效率很高，但 CEV 会快速地降到 3 × CDV 大小；当 CEV 比 3 × CDV 小时，扰动压缩效率会很低，甚至导致扰压缩失效。经过大量调整后，设定参数调整策略为同步调整CEV 与CDV，并且同步方式遵循3σ 原则。具体自适应扰动压缩流程示意如图 4 − 3 − 9 所示。图中，Last μ 为扰动压缩前的扰动中心；Lastσ 为扰动压缩前的扰动标准差；CEV 为扰动压缩时的期望修改量；CDV 为扰动压缩后的扰动标准差；SourceImage 为原始图像；TargetImage 为目标图像；StartPoint 为初始对抗样本；Nowμ 为当前迭代的扰动中心；Nowσ 为当前迭代的扰动标准差；GδS 为有效样本集。

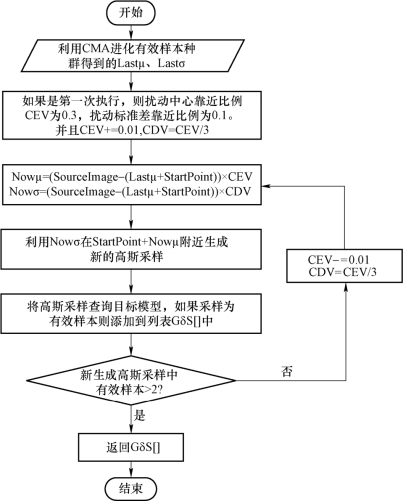
图4−3−9　自适应扰动压缩流程示意

扰动压缩的具体方法：当搜索到一个局部最优解时，将扰动期望向原始图像按照自适应的比例靠拢，同时标准差根据 3σ 原则设计为期望值的1/3，以保证定向靠近后找到的有效样本为L2 距离较小的样本而非符合原始分布的样本；如果没有找到有效样本，则减小靠拢比例，直到找到少量有效样本为止。