基于PSO的目标攻击方案优化设计

本方案的前提为给定一张原始图像x 和一个目标类 *y ，本方案的目标为生成一张视觉效果为原始图像，但被黑盒分类模型错分为目标类的目标对抗样本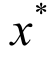。即要使对抗样本与原始图像的L2 范数尽可能小，且对抗样本被黑盒分类模型分类为目标类所对应的置信度尽可能高。

将PSO算法应用到本方案时，需要考虑的内容主要有目标图像的选取、初始种群的规模及其设定、适应度函数的设计、速度更新公式的设计以及算法终止条件。

目标图像的优劣性体现在其与原始图像的 L2 范数和其被黑盒模型分类为目标类的置信度。优劣不同的目标图像对于对抗样本的生成有较大影响，目标图像选取得越优，对抗样本的生成速度就会越快。目标图像与原始图像的 L2 距离越小，且目标图像被黑盒模型分类为目标类的置信度越高，目标图像就越优。选取较优的目标图像虽然会浪费一些黑盒分类模型查询次数，但这些查询次数在生成对抗样本的总查询次数中占比极小，因此在实验初期对目标图像进行选取是非常有价值的。

1. 初始种群生成

在生成初始种群前，需要考虑群体规模N 的大小以及初始种群的设定问题。

统计结果表明，群体规模N 一般可设置为20～40，对于特定的（或极其复杂的）问题，群体规模N 最大可以设置为100～200。在本实验中，不同的群体规模对所需查询黑盒模型的次数有一定的影响，为了明确其影响的作用大小，后续小节将给出相关实验。

初始种群的设定对于实验的成败是非常关键的，而初始种群的选取有很多种方案，因此要尽可能选出较优的种群初始化方案。本实验最初设定了两种种群初始化方案：一种是将初始种群设定在原始图像附近，此时初始种群与原始图像的L2 距离较小，但是初始种群被黑盒分类模型分类为目标类对应的置信度极小；另一种是将初始种群设定在目标图像（被黑盒分类模型分类为目标类的图像）附近，此时初始种群被黑盒分类模型分类为目标类所对应的置信度极大，但是初始种群与原始图像的L2 距离较大。在实践中发现，前一种方案很难产生理想的对抗样本，因此后续主要考虑后一种方案的可实施性。

现在已知要在目标图像附近进行初始化，但还需要考虑初始种群与目标图像的距离设定问题。本实验采用的方案为在目标图像上加入一定量的高斯噪声。初始种群的生成公式为

式中，S——初始种群；

clip(a,amin,amax)——限制数值大小函数，可将数组a 中的数值大小限制在 amin 和 amax 之间；

t——目标图像；

α ——超参数，控制着在原始图像上加入的噪声大小；

N——群体规模；

h——图像的高度；

w——图像的宽度；

3——图像颜色通道数；

rand( N , h , w, 3)——初始化每个粒子所采用的扰动随机值。

2. 适应度函数设计

从本实验的目标可知，粒子与原始图像的距离大小与其被黑盒分类模型分类为目标类所对应的置信度高低之间存在内在联系。具体而言，距离越小，粒子越优。为了使适应度函数能够对粒子的优劣进行综合评估，那么粒子的适应度函数不仅要包含以上两方面，还要在粒子与原始图像的 L2 距离越小以及粒子被分类为目标类所对应的置信度越高的情况下，计算得到越高的粒子适应值，因此本实验的适应度函数对 L2 距离取负，同时对黑盒模型返回的置信度部分取正。本实验的适应度函数可记为

式中， ftn ——适应值；

score——粒子当前所在位置的得分；

σ ——score 的权重；

L2——粒子与原始图像的L2 距离。

由前面章节给出的黑盒模型的定义，在此假定只能获取目标模型返回的top − 1 分类标签及置信度。黑盒分类模型对于对抗样本给出的标签可以分为两种情况：一种是黑盒模型返回的top − 1 分类标签 l top1是目标类 y *；另一种是黑盒模型返回的top − 1 分类标签 l top1不是目标类 y *。针对前一种情况，只需将黑盒分类模型此时返回的top − 1分类标签对应的置信度 c top1赋值给score 即可；后一种情况表明，粒子当前的所处位置是极其糟糕的，为了降低此位置的适应值，本实验采取了将score 赋值为0 的操作。目标攻击下的score 赋值为

为了使粒子的适应值能够尽可能对其综合质量进行准确评估，就不仅要考虑对score 的赋值，还要平衡score 和L2 距离的数量级。PSO 算法依据适应值选取 Pbest 和Gbest ，合理情况是适应值越大则粒子的质量越优，但是如果错误地将劣质粒子视为优质粒子，就会直接导致实验失败。本实验中的图像都进行了归一化处理，即每个像素的值都在0～1。初始种群与原始图像的L2 距离的数量级一般为2，初始种群的置信度数量级一般为 − 1，在后续的迭代过程中，置信度的数量级基本保持 − 1，L2 距离的数量级最低为1。假设适应度函数中score 和L2 距离的权重都为1，算法在运行的过程中，一个粒子的 L2 距离下降的数值一旦超过score，算法就错误地将此粒子认定为优质粒子，而粒子的 L2 距离下降的数值超过score 的情况时有发生，那么此时适应值并不能准确地反映粒子的优劣。这种情况出现的原因主要是score 和L2 距离的数量级不平衡，score 的数量级比L2 距离的小得多，因此要赋予score 一个较大的权重σ ，对score 和 L2 距离之间的数量级进行平衡，进而达到适应值越大则粒子质量越优的目的。本实验可以归纳为寻优问题，并且可以拟出适应度函数，因此尝试了将PSO 算法作为求解方案。

3. 速度更新公式设计

在对抗样本的生成中，如果只运用标准PSO 算法，将导致实验直接失败，因此要在速度更新公式中注入更多的信息。在标准PSO 算法中，速度更新公式包括惯性E、 Pbest 和Gbest 三项，但是在此方案环境下，已知要生成一个视觉效果为原始图像的对抗样本，就相当于知道粒子要达到的像素属性最优位置Ubest 。在此，Ubest 被初始化为原始图像对应的向量。为了使PSO 算法能够解决本实验情景下的问题，本实验将粒子群在每次移动的过程中都沿着Ubest 的方向靠拢，从而可以在很大程度上减少黑盒模型的查询次数。如果不加此项，则相当于对图像的行进路线没有导引，这不仅会大幅增加迭代次数，还可能导致本算法有极大可能性找不到最优解。

在加入Ubest 后，虽然可以在粒子保持有较高置信度的基础上缓慢降低L2 距离，但是PSO 算法有个极大的缺陷——非常容易陷入局部最优。为了解决此问题，本方案在速度更新公式中加入了高斯噪声。

本节实验基于PSO 的目标攻击速度解析如图4 − 2 − 3 所示。

图4−2−3　基于PSO 的目标攻击速度解析

在本实验中，粒子速度更新公式主要分为两个阶段。在初始阶段，设计了随粒子得分变化而变化的速度更新公式；在后期阶段，设计了随粒子迭代次数变化而变化的速度更新公式。

观察大量实验后发现，在迭代初始阶段的前期，粒子可以在L2 距离下降较快的情况下，依然保持和目标图像相当的得分（score），但是过了一定的迭代次数后，粒子虽然依旧能够保持较大的下降速度，但是此时粒子的得分也会大幅下降，而前期得分下降的幅度将会非常影响后期的查询次数，根据本实验适应度函数的特点，后期要使用非常多的查询次数才能将粒子得分缓慢提升。因此，在实验的初始阶段要对粒子的得分有所把控，然后据此来设计速度更新公式。本实验初始阶段设计的随粒子得分变化而变化的速度更新公式包含五部分：惯性E、Pbest、Gbest、Ubest、高斯噪声。公式为

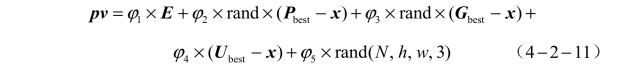
式中，φ1为惯性权重函数；φ2为认知学习因子函数；φ3为社会学习因子函数；φ4为Ubest权重函数；φ5为高斯噪声权重函数；式中的所有权重函数都与粒子得分有关。

当粒子群的平均得分小于一定的数值后，粒子群就进入后期迭代阶段。在此阶段，设计了随粒子迭代次数变化而变化的速度更新公式，这一阶段的速度更新公式中只包含惯性E、Gbest、Ubest和高斯噪声四项，而没有加入Pbest这一项，主要使用Gbest来引导粒子向已知的最优位置靠近。这一阶段的速度更新公式为

式中，φ1′为本阶段的惯性权重函数；φ3′为本阶段的社会学习因子函数；φ4′为本阶段的Ubest权重函数；φ5′为本阶段的高斯噪声权重函数；式中的所有权重函数都与粒子的迭代次数有关。

有了粒子当前的移动速度pv，就可以根据公式来更新粒子的位置X，即

本算法不仅会记录每个粒子的Pbest和整个粒子群的Gbest，还会分别对其适应值进行记录，因为本算法是通过粒子的适应值来比较其优劣。本节将Pbest对应的适应值标记为PbestFtn ，将Gbest对应的适应值标记为GbestFtn 。本节通过初始种群中的每个粒子及其对应的适应值分别对每个粒子的Pbest和PbestFtn 进行了初始化，Pbest和PbestFtn 的初始化公式分别为

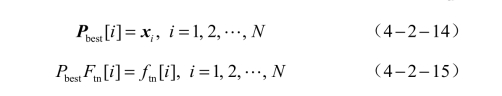
式中，xi——粒子群中的第i个粒子；

Pbest[i ]——第i个粒子的最优个体；

N——群体规模；

PbestFtn[i]——第i个粒子的个体最优值对应的适应值；

ftn[i]——第i个粒子当前位置的适应值。

由于Gbest是从所有的Pbest中选取的最优值，因此Gbest的初始化不仅包含赋初值操作，还包含更新操作。同时，Gbest对应的适应值GbestFtn 也进行初始化操作。本节实验采取的Gbest和GbestFtn 赋初值操作为将第一个粒子的Pbest 及PbestFtn 分别赋值给Gbest和GbestFtn 。Gbest和GbestFtn 的赋初值操作分别为

对于Gbest和GbestFtn 的更新，需要将粒子群中每个粒子的PbestFtn 与GbestFtn进行比较，进而得到整个粒子群的全局最优值，以及对应的适应值。初始化中Gbest和GbestFtn的更新公式分别为

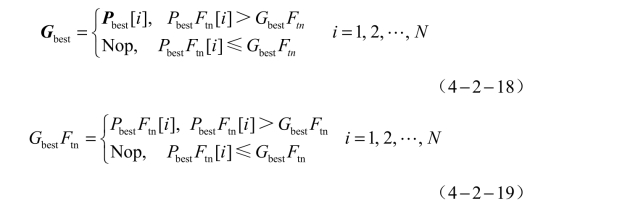
式中，Nop——无操作。

本方案在每次迭代的过程中要对每个粒子的bestP和群体的bestG进行更新，以便了解当前的个体最优位置和全局最优位置，bestP和bestG均依据PbestFtn 和GbestFtn 进行更新，因此在每次迭代中还要对PbestFtn 和GbestFtn进行更新。在每次迭代中，Gbest和GbestFtn的更新也是根据式（4 − 2 − 18）和式（4 − 2 − 19）进行的。每个粒子的Pbest和PbestFtn 的更新公式分别为

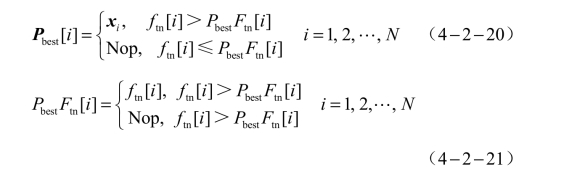
4. 算法终止条件

本方案的主循环体设置了两个判断条件。 (www.xing528.com)

根据黑盒模型的定义可知，攻击方不能对黑盒模型进行无限次数的查询，因此本节实验设置了最大可查询次数V，于是第一个判断条件为判断当前查询次数q是否已超出最大可查询次数V，即

如果qV＞，则表明目标对抗样本生成失败，此时算法终止，并返回目标对抗样本生成失败的信息，以及当前效果最好的生成失败的目标对抗样本。

当满足第一个判断条件后，就继续执行算法过程代码，然后对第二个条件进行判断。第二个判断条件为

式中，L2——粒子当前所在的位置与原始图像的L2距离；

ε——对抗样本的扰动上限；

score——粒子当前所在位置的得分；

β——对抗样本的置信度下限。

当粒子当前所在的位置与原始图像的L2距离下降到对抗样本的扰动上限ε后，同时此粒子被黑盒模型分类为目标类，且目标类所对应的置信度也高于对抗样本的置信度下限β 后，则表明目标对抗样本生成成功，此时算法终止，并返回目标对抗样本生成成功的信息，以及成功生成的目标对抗样本。

本节实验的基于 PSO 的目标攻击下算法终止条件判断流程如图 4 − 2 − 4 所示。

图4−2−4　目标攻击下算法终止条件判断流程

5. PSO 的目标攻击算法具体流程

黑盒分类模型下基于 PSO 的目标攻击算法见算法 4 − 2 − 1。其中，主要融合了初始种群生成、适应度函数、速度更新公式和算法终止条件。

在给定的查询次数内找到符合条件的对抗样本时（即成功找到对抗样本时），该算法将直接对成功生成的对抗样本进行输出；当查询次数用完但并未找到符合条件的对抗样本时，为了掌握此种情况下对抗样本的生成效果，该算法对此时找到的最优图像进行输出，即对当前的Gbest 进行输出。

6. 实验配置

1）实验环境介绍

本节涉及的所有实验都是在如表4 − 2 − 1 所示的硬件环境下完成的。因为GPU 比CPU 能够更好地支持深度学习方面的计算，所以本节所有实验中的计算任务主要都在GPU 上完成。

表4−2−1　实验硬件环境

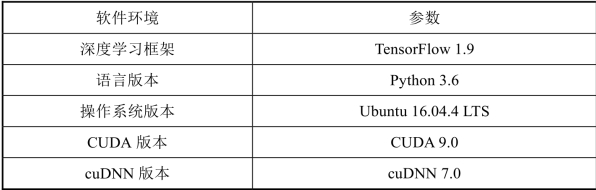
本节的所有实验都是在深度学习框架 TensorFlow 上进行的。由于TensorFlow 的架构极其灵活，因此用户能够很容易地将计算内容部署到CPU、GPU 或者TPU 等平台以及设备上。本节涉及的所有实验在计算过程中处理的数据量几乎都处于百万数量级，因此计算速度是非常值得考虑的问题之一。为了提升算法的计算速度，一方面，代码要足够简练；另一方面，计算机的GPU 等硬件设备要能够充分地利用。为了提升GPU 的运算速度，本节涉及的所有实验都采用了英伟达公司推出的一款名为CUDA 的计算架构，同时为了使 GPU 能够计算深度学习领域的数据，本节涉及的所有实验都使用了cuDNN。本节所有实验采用的软件环境如表4 − 2 − 2 所示。

表4−2−2　实验软件环境

在黑盒模型和原始图像的选取方面，本节实验选取的黑盒分类模型为Inception v3。Inception v3 模型是基于 ImageNet 训练集和验证集得来的（众所周知，ImageNet 测试集、训练集以及验证集基本服从同一分布）。为了让实验更有说服力，本节实验选取的图像都要能够被黑盒分类模型正确分类，如果黑盒分类模型对原始图像的分类最初就是错的，那么后期就无法对对抗样本的成功率进行判断，因此本节实验中的原始图像都是从ImageNet 测试集中随机选取出来的。此外，本节实验中的目标图像也都是从ImageNet 测试集中随机选取出来的。从ImageNet 测试集中随机选取原始图像和目标图像的好处是在保持实验真实性的前提条件下，减少实验前期对图像的筛选工作。

2）实验参数设定

本节实验主要包括种群初始化、适应度函数、速度更新公式以及算法终止条件四个部分，各部分参数设定如下。

（1）种群初始化中的参数设定：在具体的实验中，给定的原始图像和目标图像的高度h、宽度w 都设置为299；群体规模N 设置为3，但是为了证实不同的群体规模对于黑盒模型查询次数的影响，本节实验将群体规模N 分别设置为不同的数值并进行了对比实验；初始种群生成公式中的噪声权重α 采用0.01。

（2） 适应度函数中的参数设定：置信度在适应度函数的权重σ 采用15，原因是score 最初非常接近于1，不同的原始图像与目标图像对最初的L2 距离平均在 100～300（归一化后），因此为了在适应度函数中平衡这两个变量的数量级，将σ 设置为 15。而且在后续的迭代过程中，score 的数量级都基本保持为 − 1，L2 距离的数量级也基本处于 2～3，所以将σ 设置为15 在整个实验的过程中都是可行的。

（3）算法终止条件中的参数设定：最大可查询次数V 被设置为800 000；对抗样本的置信度下限β 采用0.8；本节实验将和NES + PGD 方法作比较，NES + PGD 方法设定的扰动上限是 0.05 的L∞距离，而本节实验是基于 L2距离进行判定，因此本节实验对抗样本扰动上限ε 的设定将由给出，将h 和w 的值代入此函数后计算得25.9。本节实验为了降低对抗样本扰动大小，将对抗样本扰动上限ε 设置为25。

7. 群体规模对查询次数的影响

为了验证不同大小的群体规模在生成对抗样本时对所需黑盒模型查询次数的影响，在此将选定的一对原始图像和目标图像运行在多组不同的群体规模下来进行验证。

所选取的原始图像和目标图像对如图 4 − 2 − 5 所示。其中，图 4 − 2 − 5（a）为选定的原始图像，其被黑盒分类模型以0.848 2 的置信度分类为goose；图4 − 2 − 5（b）为选定的目标图像，其被黑盒分类模型以0.897 4 的置信度分类为wood rabbit。

图4−2−5　目标攻击下的原始图像和目标图像对

（a）原始图像（goose: 0.848 2）；（b）目标图像（wood rabbit: 0.897 4）

这部分实验将群体规模 N 分别设定为 3、5、10、15、20、25 六个不同的取值，基于图4 − 2 − 5 给定的数据所作的群体规模对查询次数影响的折线图如图4 − 2 − 6 所示。其中，每种颜色的折线对应一个群体规模数值，因此该图中共有6 条折线。图中的横坐标为黑盒模型查询次数，纵坐标为当前图像与原始图像的L2 距离。从中可以看到，随着黑盒模型查询次数的增加，当前图像与原始图像的L2 距离在逐渐缩小。

由图4 − 2 − 6 可以得出结论：随着群体规模N 的增加，在生成对抗样本的过程中所需的黑盒模型查询次数呈递增趋势。在成功生成对抗样本时，群体规模为25 时所需的黑盒模型查询次数是群体规模为3 时所需的黑盒模型查询次数的2.5 倍。因此，为了尽可能减少黑盒模型查询次数，本节实验都基于群体规模为3 进行。

图4−2−6　群体规模对查询次数的影响（书后附彩插）

8. 不同的目标图像对查询次数的影响

不同目标图像之间的差异，主要体现在其被黑盒模型分类为目标类所对应的置信度的不同，以及其与原始图像的L2 距离的不同。为了验证不同目标图像之间的这两方面差异对于黑盒模型查询次数的影响，在此设计了两组实验来进行验证。第1 组选取的是置信度基本一致，但是L2 距离差异较大的目标图像集；第2 组选取的是L2 距离基本一致，但是置信度差异较大的目标图像集。

第1 组实验选取的原始图像和不同L2 距离的目标图像集如图4 − 2 − 7所示。其中，最左侧的图像为原始图像，（a）～（f）为选定的目标图像集（标签均为starfish），每张目标图像的上方都标识着其被黑盒分类模型分类的标签及其置信度，L2 表示其自身与原始图像的 L2 距离，（a）～（f）的L2 距离依次增大。

基于图4 − 2 − 7 中的数据，不同L2 距离的目标图像对黑盒模型查询次数的影响折线图如图4 − 2 − 8 所示。其中，横轴为黑盒模型的查询次数，纵轴为当前图像与原始图像的L2 距离，图例（a）～（f）分别对应图4 − 2 − 7中的目标图像（a）～（f）。从图 4 − 2 − 8 中的折线可以看出，随着黑盒模型查询次数的增加，其与原始图像的L2 距离都在逐渐减小。

图4−2−7　原始图像和不同L2 距离的目标图像集

图4−2−8　不同L2 距离的目标图像对黑盒模型查询次数的影响（书后附彩插）

观察这6 条折线可大致总结出规律：与原始图像L2距离越小的目标图像，在成功生成对抗样本时所需的黑盒模型查询次数越少。本节实验选取的L2距离最小的目标图像（a）和L2距离最大的目标图像（f），在L2距离都下降到25 的情况下，目标图像（f）比目标图像（a）所需的黑盒模型查询次数多近15 000 次。

第2 组实验选取的原始图像和不同置信度的目标图像集如图4 − 2 − 9所示。其中，最左侧的图像为原始图像，（a）～（f）为选定的目标图像集（标签均为 umbrella），每幅目标图像的上方都标识着其被黑盒分类模型分类的标签及其置信度，以及其自身与原始图像的L2 距离，（a）～（f）被黑盒分类模型分类的置信度依次增大。

图4−2−9　原始图像和不同置信度的目标图像集

基于图4 − 2 − 9 中的数据，不同置信度的目标图像对于黑盒模型查询次数的影响折线图如图4 − 2 − 10 所示。其中，横轴为黑盒模型查询次数，纵轴为当前图像与原始图像的 L2 距离，图例（a）～（f）分别对应图 4 − 2 − 9中的目标图像（a）～（f）。从图4 − 2 − 10 中的折线可以看出，随着黑盒模型查询次数的增加，其与原始图像的L2 距离都在逐渐减小。

图4−2−10　不同置信度的目标图像对黑盒模型查询次数的影响（书后附彩插）

本案例中出现了一个个例——被黑盒分类模型分类为目标类的置信度最小的目标图像（a）在所有的目标图像中脱颖而出，但这并不能代表总趋势。观察其他5 条折线，可大致总结出规律：被黑盒分类模型分类为目标类的置信度越高的目标图像，在成功生成对抗样本时所需的黑盒模型查询次数越少。只因置信度不同，在成功生成对抗样本时，目标图像（b）比目标图像（f）所需的黑盒模型查询次数要多70 000 次。

从这两组实验中可以发现，被黑盒模型分类为目标类所对应的置信度越高、与原始图像的L2 距离越小的目标图像，在生成对抗样本的过程中优势越明显。因此在进行目标攻击时，攻击方可按以上规律对目标图像进行选取，此操作可在很大程度上减少黑盒模型查询次数。