粒子群优化算法：思想和应用

Eberhart 和 Kennedy[54]提出的粒子群优化算法是一种寻优算法，通过粒子在不断地迭代进化中找到越来越优的位置，最终得到最优解。

整个粒子群能够移动起来的重要前提是知道每个粒子在迭代到不同位置时的优劣情况。对其的优劣评判可以从适应值得到，适应值越高则表示当前位置的粒子越好，而适应值可通过适应度函数计算得到。在PSO 算法中，适应度函数的设计是至关重要的。首先，适应度函数的每项都要能够对粒子当前位置某方面的优劣有所体现；其次，对各项组成部分进行综合之后，要能对粒子当前位置的优劣进行综合、准确的评估。值得一提的是，适应度函数各项组成部分的权重设置也是举足轻重的。适应度函数的重要性体现在PSO 算法的收敛速度上，同时适应度函数也决定着能否找到最优解。

PSO 算法的主体是一群粒子，且粒子的形式因实验目标而异，这是在做实验之前应首先考虑的。在PSO 算法中，粒子形式和最优解形式是相同的，例如，最优解是一个200 维的向量，那么粒子群中的每个粒子也必须是200 维的向量。通过之前实验给出的相应目标可知，无论目标模型是黑盒分类模型还是黑盒目标检测模型，最终的目标都是得到一幅样本图像，因此在本节涉及的实验中，每个粒子代表的都是一幅图像。

在PSO 算法的执行过程中，首先要对种群进行初始化，粒子群接下来的每一次移动都在速度更新公式的指导下进行，不同的速度更新公式对于粒子群的移动有着不同的促进效果。

假设目标搜索空间为W 维，W 为一幅图像中包含的像素总数的 3 倍（每个像素点都有RGB 三个通道）；粒子群中包含N 个粒子，每个粒子都是一幅图像。那么，第i 个粒子是一个W 维向量，可以记为

式中，Xi ——图像群中的第i 幅图像；

x ——图像群中第i 幅图像的第

iW个像素点上的第W mod 3 个颜色通道上的数值。

第i 个粒子的移动速度也是一个维度为W 的向量，记为

式中， Vi——图像群中第i 幅图像的移动速度，即每个像素颜色值的数值变化大小；

vi W ——图像群中第i 幅图像的第个像素点上的第W mod 3 个颜色通道上的数值变化大小。

第i 个粒子到目前为止所找寻到的最优位置称为个体最优值（personal best），记为

式中， Pbesti ——图像群中第 i 幅图像在之前移动过程中到目前为止所找寻找到的最优图像。

pi W —— Pb esti的第个像素点上的第W mod 3 个颜色通道上的数值。

整个粒子群中的所有粒子到目前为止所找寻到的最优位置称为全局最优值（global best），记为

(www.xing528.com)

式中， Gbest ——整个图像群到目前为止所找寻到的最优图像；

pg W——找到的最好的那幅图像的像素值。

假设当前迭代次数为k，第i 个粒子在获取 Pbest 以及整个粒子群的 Gbest后，再加上本粒子的惯性，即可根据式（4 − 2 − 5）计算得到本粒子第k+1次迭代的移动速度。

式中，,——第i 幅图像在第k+1 次、第k 次的移动速度；

ω, c1 , c2 ——权重；

rand——随机数；

——第i 幅图像在移动k 次后得到的 ；

——第i 幅图像第k 次移动之后的图像；

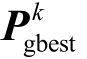——整个图像群在进行第k 次移动后所找到的最优图像。

式（4 − 2 − 5）由三部分组成：

第一部分为本粒子的惯性，也就是粒子上一次迭代的移动速度，此部分体现了粒子的运动习惯，表明粒子的运动过程在一定程度上保持了上一次迭代的运动速度，因此本项的权重ω 称为惯性权重。

第二部分为粒子的“认知”部分，即粒子在之前的移动过程中所总结的自身经验，粒子本身的经验知识对粒子的下一次优化起着至关重要的作用，此项的权重 c1 被称为认知学习因子。

第三部分为粒子的“社会”部分，这一部分的信息是由整个粒子群在进行信息共享后所总结得到的社会经验，所有粒子都通过此社会经验向迄今为止的最优位置靠拢，因此此项的权重 c2 被称为社会学习因子。

式（4 − 2 − 5）为 PSO 算法的标准形式，标准 PSO 速度解析如图 4 − 2 − 1 所示。

有了粒子当前的移动速度，即可根据式（4 − 2 − 6）更新粒子的位置。

图4−2−1　标准 PSO 速度解析