对抗样本攻击下的可微分类器优化算法

本节通过三部分实验来评估DDN 攻击算法。

（1） 在非目标攻击环境下，将 DDN 攻击算法与 C&W 攻击算法、DeepFool 攻击算法在不同迭代预算下的攻击效果进行比较。

（2） 在目标攻击环境下，将DDN 攻击算法与C&W 在不同迭代预算下的攻击效果进行比较。

（3） 将改进 DDN 攻击算法参数后（DDN′）的攻击效果与原 DDN 攻击算法和C&W 攻击算法在相同迭代预算下的攻击效果进行比较。

DDN 攻击算法优化一个交叉熵损失函数，与C&W 攻击算法不同的是，它在迭代查询过程中不使用惩罚因子来约束L2 范数，而将每一次迭代生成的扰动投影到一个以原始图像为球心的L2 球体上。然后，范数的变化取决于样本是否具有对抗性。使用这种方法来分离敌方噪声的方向和范数，会导致只需要极少迭代的攻击，就可以达到与最新技术相当的性能水平，同时易用于对抗训练。

1. 目标公式

将原始图像x 作为输入空间X 的一个原始样本，具有真实分类标签 ytrue（来自标签集Y），　D (x1,x2 )表示输入图像 x1 和 x2 之间的距离， P (y | x , θ ) 表示以θ 为参数的分类器（模型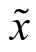），表示对抗样本，使达到arg max j（非目标攻击）且，其中ε 是预设的最大扰动限制，yj 为输出的最高置信度的分类，其分类标签为j。在目标攻击情况下，需要满足, ytarget为目标分类标签。对于输入模型的原始图像x 和给定标签y，设置一个交叉熵损失函数 J (x , y , θ )，用于衡量以θ 为参数的分类器对于输入图像 x 给出的分类标签与给定标签 y 之间的损失。图 4 − 1 − 1 所示为在 Inception v3 模型[47]上对 ImageNet 数据集实施目标攻击的结果：原始图像x 的分类为curly hound，在添加一个扰动δ 后，被分类器分类为microwave oven。

图4−1−1　ImageNet 数据集上对抗样本示例

（a）原始图像，分类为curly hound；（b）添加的扰动；（c）对抗样本，分类为microwave oven

通常，认为攻击是由基于梯度的优化过程产生的，这限制了我们对可微分类器的分析。这些攻击可以被公式化为获得最小的扰动或者在限制下得到最大损失。

假设用于衡量原始图像和对抗样本之间的距离函数为一个范数（ L0 、L2 或 L∞），输入为图像，图像的各像素被限制在 0～M。在一个白盒环境下，使用非目标攻击并且预期得到最小扰动的公式描述为

式中，δ ——在原始图像上添加的扰动；

M ——设定的最大扰动。

目标攻击的公式化与之相似，使分类器的输出结果与目标类相同即可。

如果算法目的在于得到在一定范数限制下的最大损失，则解决该问题的公式可以描述为

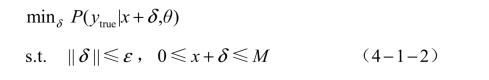
目标攻击的公式化与之相类似，最大化即可。

将主要目标聚焦在基于梯度的方法来优化扰动的范数，虽然这种距离不能完全捕获感知的相似性，但在计算机视觉中广泛应用于测量图像之间的相似性。例如，在比较图像压缩算法中使用峰值信噪比，这与二级测量直接相关）。捕获感知相似性的可分辨距离测量仍然是一个开放的研究课题。

2. 威胁模型

在设计算法时，仅考虑白盒情况下的攻击。在这种情况下，可认为攻击者对系统内部结构掌握了充分的知识，包括其中的神经网络结构和参数权重。该威胁模型用于评估最坏情况下的系统安全性。其他场景可以设想为根据攻击者的知识在不同的假设下评估攻击，如无法访问训练模型、无法访问同训练集等。这些场景被称为黑盒或有限的知识。

3. 详细设计

从问题的定义来看，在一个固定的区域找到最坏的对抗样本是一项更容易的任务。在式（4 − 1 − 2）中，这两个约束都可以用δ 表示，并且可以使用投影梯度下降来优化。找到与原始图像最接近的对抗样本较困难——式（4 − 1 − 1）对模型的预测有限制，这不能通过简单的投影来解决。Szegedy等人使用了一种常用方法（这个方法同样使用在C&W 攻击算法中），即将式（4 − 1 − 1）中的约束问题近似为无约束问题，将约束替换为惩罚因子。这相当于用一个足够高的参数 C 联合优化了两个术语——δ 范数和一个分类术语。在约束优化的一般情况下，这种基于惩罚的方法是一个众所周知的原则[53]。在解决无约束问题的同时，惩罚方法在实践中也存在着众所周知的困难，主要困难是必须以一种特殊的方式选择参数C。例如，如果C太小，则产生的样本不会具有对抗性；如果C 太大，则该参数将占主导地位，并导致算法所产生的对抗样本的扰动更大。这在使用少量步骤进行优化时尤其有问题（例如，在对抗性训练中使用）。图4 − 1 − 2 所示为通过对MNIST 数据集运行C&W 攻击算法获得的C 值的柱状图。由该图可以发现，C 的最佳值在 2−11～25 范围内变化很大；同样可以观测到，对于最佳的常数 C，其对应的扰动无论是否经历过对抗训练的模型都产生了变化（对抗训练模型通常要求一个高数值的C）。此外，通过添加惩罚因子的方式来限制范数将导致收敛速度慢。

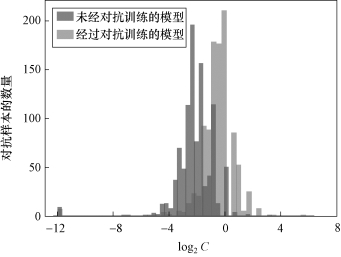
图4−1−2　最佳 C 值柱状图(www.xing528.com)

针对这种优化算法难以找到合适的常数的问题，本实验提出了一种在优化过程中对L2 范数不加惩罚的算法。作为替代，先将每一次迭代生成的扰动投影到一个以原始图像为球心的L2 球体上，再通过二元决策来修改这个范数，决策基于生成的样本是否具有对抗性。假设样本 xk 在迭代次数为k 时不具有对抗性，那么在k + 1 步的范数将增长；否则，将降低。另外，优化交叉熵可能带来另外两个困难：其一，函数不受约束，这使它在优化问题中占主导地位；其二，在攻击训练模型时，原始图像的正确类的预测概率通常非常接近 1，这导致交叉熵在搜索对抗样本时的起点非常低，并最终可能增加几个数量级。这些困难会影响梯度的范数，导致很难找到合适的学习速率。C&W 攻击算法通过优化logits 层之间的差距而不是依靠交叉熵来解决这些问题。在这项工作中，无边界问题不影响攻击过程，因为更新范数的决策是在模型的预测上完成的（而不是在交叉熵上）。为了解决梯度范数变化大的问题，首先将梯度归一化为单位范数，然后向其方向迈出一步。

DDN 攻击算法的步骤见算法 4 − 1 − 1。

非目标攻击的图像说明如图4 − 1 − 3 所示，图中的阴影部分区域表示被分类为 ytrue 的输入样本空间。在图 4 − 1 − 3（a）中， x˜k不具有对抗性，因此根据算法来提高下一轮迭代的范数ε k+1 ；相对而言，在图4 − 1 − 3（b）中降低了范数。在这两种情况下，每一次变化都从当前起点 x˜k处沿着梯度 g方向前进g，然后投影到一个以x 为中心的ε k+1 球体上。

图4−1−3　非目标攻击的图像说明（书后附彩插）

（a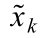）没有对抗性；（b） 有对抗性

DDN 攻击的完整过程可通过图4 − 1 − 3 来说明。从原始图像x 出发，迭代地修改噪声 δ k。在第 k 次循环时，若当前生成的样本仍然不具有对抗性，则根据算法来修改下一步范数。否则，通过来降低范数。在这两种情况下，每一次的变化都从当前起点处（图 4 − 1 − 3 的红色箭头）沿着梯度 g 方向前进（算法 4 − 1 − 1 的步骤5），然后投影（图4 − 1 − 3 的蓝色虚线）到一个以x 为中心的ε k+1 球体上，获得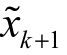。最后，将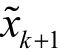投影到输入空间X 的可行区域上。对于要求标准化到[0,1]的图像，只需将每个像素的值映射到该范围内（算法4 − 1 − 1 的步骤13）。此外，还可以考虑在每次迭代中对图像进行量化，以确保攻击的是有效的图像。

值得一提的是，当某一次迭代产生的对抗样本 x˜k的球体与决策边界相切时，g 就会和扰动δ k+1 沿相同的方向。这就意味着扰动δ k+1 将投影到 kδ 的方向，由此导致范数沿该方向在决策边界的两边摆动。重复步骤εk　+ 1 = (1 +　γ )εk 和εk　+1 = (1 −　γ )εk，将导致全局递减，即范数乘以一个比 1小的数　1 − γ2来找到最好的范数值。

本节实验在数据集 MNIST、CIFAR − 10 和 ImageNet 上进行验证，并将该DDN 攻击算法与已经在文献中提出过的最先进的使用L2 范数进行约束的算法——DeepFool 攻击算法和C&W 攻击算法进行比较。本节实验使用与MNIST 和 CIFAR − 10 相同的模型体系结构和相同的超参数进行训练，详见表 4 − 1 − 1。本节实验的基本分类器在数据集 MNIST 和CIFAR − 10 的测试集上分别获得99.44%和 85.51%的精度。对于ImageNet数据集，本节实验使用了一个预先训练的Inception v3[47]，在验证集上实现22.51%的前一个错误。Inception v3 以299 像素 × 299 像素的图像为输入，从342 像素 × 342 像素的图像中映射。

表4−1−1　用于攻击评估的 CNN 结构

对于使用DeepFool 攻击算法进行的实验，使用了Foolbox 中的实现部分，其中预算部分为100 次迭代；对于使用C&W 攻击算法进行的实验，将攻击移植到PyTorch 上来评估训练框架中的模型。本节实验所用的超参数为典型的C&W 9 × 10 000 场景，即初始常数为0.01，设定9 个搜索步骤，设置迭代次数为10 000 次（提前停止）。为了与DDN 攻击算法进行比较，需要C&W 攻击在迭代次数较少的情况下的攻击结果，于是设置了迭代100次的实验。在设定100 次迭代的基础上，分为4 × 25 和1 × 100 两部分。由于文献［48, 52］中给出的超参数只适用于迭代次数较大的情况，因此使用［0.01，0.05，0.1，0.5，1］内的学习率和［0.001，0.01，0.1，1，10，100，1 000］内的C 值对每个数据集进行网格搜索。通过实验验证，C&W 攻击算法的超参数选择情况如表 4 − 1 − 2 所示。

表4−1−2　C&W 攻击算法的超参数选择

续表

对于使用DDN攻击算法的实验，选择迭代次数分别为100、300、1 000次的攻击，在所有攻击场景中都使用0 1ε=和0.05γ=，初始步长1α=，并随着余弦退火调整学习率逐渐降低到0.01。γ的选择基于图像的编码技术，对于任何正确分类的图像，最小可能的干扰包括将一个像素更改1/255（对于以8位值编码的图像）对应于1/255的范数。由于在此执行量化，所以对值四舍五入，这意味着算法必须能够实现低于1.5/255 = 3/510的范数。当使用k次迭代时，就要求：

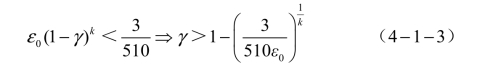
式中，0ε——初始扰动范数；

γ——调整扰动范数的参数。

由0 1ε=和100k=，得出0.05γ=。因此，如果存在干扰最小的对抗样本，那么算法就可以通过固定的步骤找到它。

对于DDN攻击的结果，我们考虑量化图像（到256级）。量化步骤包含于每次迭代中（参见算法4 − 1 − 1的步骤13）。本节得到的所有结果都考虑了[0,1]范围内的图像。本节实验进行了两组实验：非目标攻击和目标攻击。对测试集MNIST和CIFAR − 10的前1 000幅图像生成了攻击，而对于ImageNet测试集，是从正确分类的验证集中随机选择了1 000幅图像。对于非目标攻击，报告了攻击的成功率（发现攻击的样本百分比）、对抗噪声的平均L2范数（成功攻击的平均L2范数）和所有攻击的中间L2范数。还报告了在有8 GB 内存的NVIDIA GTX 1080 上梯度计算的平均数（对于批处理执行）和总运行时间（以秒为单位）。

实验结果分析中不包括 DeepFool 攻击的运行时间，这是因为从Foolbox 中实现了一个接一个地生成对抗样本，并在GPU 上执行，因此无具有代表性的运行时间。

对于目标攻击的实验，在数据集MNIST 和CIFAR − 10 上，将本节实验设计为对所有可能的分类进行攻击（即每幅图像攻击 9 次）；而在ImageNet 数据集上，由于标签总数有1 000 个，若全部攻击，将耗费大量的时间和计算代价，于是随机选择100 个其他分类（总分类的10%）。因此，在每次目标攻击实验中，在数据集MNIST 和CIFAR − 10 上运行9 000 次攻击，在ImageNet 数据集上运行100 000 次攻击。报告的结果分为两部分：其一，所有攻击的平均范数；其二，在选择最低可能分类时的平均性能（比如对每一幅图像选择其最不可能的分类）。对于非目标攻击的场景，实验得出的L2 范数是所有攻击成功的结果的平均值。