了解火箭弹的工作原理 或 探秘火箭弹的运作方式

火箭弹是靠火箭发动机产生的反推力而运动的，因此火箭发动机是火箭弹的动力推进装置。火箭发动机的工作原理即火箭弹的推进原理。当火箭发射药被点燃时，火箭发动机便开始工作。固体火箭发动机的工作原理如图10-8所示。

图10-8　固体火箭发动机的工作原理

固体火箭发动机的工作过程：在火箭弹发射时，发火控制系统使点火具发火，而点火具中药剂燃烧时产生的燃气流经固体推进剂装药表面时将其点燃。主装药燃烧产生的高温高压燃气流经固体火箭发动机中拉瓦尔喷管时，燃气的压强、温度及密度下降，流速增大，在喷管出口截面上形成高速气流向后喷出。当大量的燃气以高速从喷管喷出时，火箭弹在燃气流反作用力的推动下获得与空气流反向运动的加速度。显然，火箭弹运动时，其相互作用的物体中，一个是火箭弹本身，另一个是从火箭发动机喷出的高速燃气流。由此可见，火箭弹的这种反作用运动为直接反作用运动。高速燃气流作用在火箭弹上的反作用力为直接反作用力，使火箭弹获得向前运动的推力。当固体火箭发动机结束工作时，火箭弹在弹道主动段末端达到最大速度。

当固体火箭发动机工作时，所产生的大量的燃气以很高的速度向后排出。由于抛出的物质是火箭发动机所携带的固体推进剂装药燃烧产生的，所以火箭发动机的质量不断地减小，这表明火箭弹的运动属于变质量物体运动。关于作用在火箭发动机上的反作用力公式，可以利用动量定理求解。

对图10-9所示的火箭系统，设火箭在某瞬时t时，质量为m，速度为v，此时火箭动量为mv；火箭经过Δt时间之后，在t+Δt时，质量变为m-Δm，速度变为v+Δv，此时火箭系统（包括火箭壳体和燃气）的动量为

（m-Δm）（v+Δv）+（-Δm·ω）=（m-Δm）（v+Δv）-Δm［ve-（v+Δv）］

图10-9　推导火箭运动方程示意

式中　ω——燃气排出的绝对速度，m/s；

ve——燃气质点相对于火箭的速度，m/s。(www.xing528.com)

在Δt内火箭动量的变化（略去二次微量）情况如下：

｛（m-Δm）（v+Δv）-Δm［ve-（v+Δv）］｝-mv=mΔv-Δmve

由动量定理可得

mΔv-Δmve=Δt∑pi

两边各除以Δt，并取极限和移项，得

式中　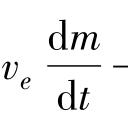——单位时间内由于质量变化而产生的动量变化，我们称之为反作用力。这个反作用力是在火箭发动机工作时产生的，是推动火箭运动的主力。它是火箭发动机推力F的主要部分。∑pi是作用在火箭纵轴方向上的空气阻力、重力、大气压力以及作用在喷管排气面上燃气压力之和。

式（10-1）是变质量运动微分方程，也称梅歇尔斯基方程式。这个方程由俄国学者梅歇尔斯基在1897年推出并发表。

由此可见，当大量的气体从喷管高速喷出时，火箭弹在火箭发动机的推力作用下高速向前运动。与炮弹不同，火箭弹的发射装置（如火箭筒）只赋予火箭弹一定的射角、射向并提供点火机构，使动力装置开始工作，但发射装置并不提供使火箭弹飞行的初始速度。火箭弹与目前使用的火箭增程弹也不同。火箭增程弹是采用火箭发动机增程的炮弹，即火箭增程弹首先由火炮提供一定的初始速度将其发射出去。出炮口一定距离后，火箭发动机开始工作。弹丸在推力作用下继续加速，使射程增加。在火箭发动机工作以前的运动与普通炮弹一样；而在火箭发动机开始工作以后，则和普通火箭弹相同；当火箭发动机工作结束后，又和普通炮弹的运动规律一致。