射击精度与焊接氧化焰的相关介绍

这里所说的精度是指射击精度。射击精度是指射弹的弹着点（或炸点）同预期命中点间接近程度的总体度量，包括射击准确度和射击密集度两个方面。只有射击准确度和射击密集度都好，才能说射击精度好。弹着点对预期命中点的偏差被称为射击偏差，也称为射击误差。射击偏差是衡量射击精度的尺度，是由诸元偏差与散布偏差引起的。诸元偏差影响射击准确度，散布偏差影响射击密集度。

（1）射击准确度

射击准确度，表示射弹散布中心对预期命中点的偏离程度。这种偏离是由在射击准备过程中测地、气象、弹道等方面的误差、射表误差和武器系统技术准备误差等综合产生的射击诸元误差造成的，通常被称为诸元偏差，因此射击准确度又叫诸元精度。诸元偏差在一次射击中是不变的系统误差，可以通过校正武器或者修正射击诸元来缩小或者消除。射击准确度通常用诸元概率偏差来表征，且其值越小，射击准确度越好。诸元概率偏差通常采用理论与试验相结合的方法来确定。在枪械射击中，射击准确度一般用平均弹着点偏离预期命中点的距离来近似度量。这个距离越小，射击准确度就越好。平均弹着点是一定数量弹着点分布空间的中心位置。在弹着点无限多时它就是射弹散布中心。

（2）射击密集度

当在相同的射击诸元条件下，用同一批弹药对同一目标进行瞄准射击时，这些弹药无论在什么情况下都不会命中同一目标，即使事先对各发弹都仔细进行了挑选，各发弹的弹道也不会重叠在一起，而是形成一定的弹道束，落在一定的范围内，这种现象叫射弹散布。

射击密集度，表示各个弹着点对散布中心偏离程度的总体度量。这种偏离来源于各发射弹发射时武器、弹药、气象、发射操作及其他有关因素的非一致性造成的各不相同的随机偏差。这种偏差，会引起射弹散布，也叫散布偏差，因此射击密集度也叫散布精度。它是射弹散布疏密程度的表征。由于散布偏差只能设法减小，不能完全消除，故射弹散布是不可避免的。

①射弹散布产生的原因。

总的来说，引起射弹散布的原因大体可分为3类：

一是各发弹的特征系数（如弹丸质量、弹径、弹长、质心位置、质量偏心和外形等）稍有不同并表现为随机性质。

二是各发弹的射击条件（如初速、射角、射向和发射药量等）稍有不同并表现为随机性质。

三是各发弹所受到的干扰（如初始扰动、气象条件、气动偏心和火箭弹的推力偏心等）稍有不同并表现为随机性质。

所有这些因素的综合作用结果，使射弹的实际弹道形成散布，如图1-10所示。

②射击密集度的度量方法。射击密集度通常有3种度量方法，即射弹散布概率偏差、散布密集界和散布圆半径或圆概率偏差（CEP）。

射弹散布概率偏差：射弹散布概率偏差，也称射弹散布概率误差、射弹散布中间偏差或公算偏差。在射弹散布面上，与散布轴对称，弹着点出现概率为50%的区间宽度的一半称为射弹散布概率偏差，如图1-11所示。有高低、方向和距离射弹散布概率偏差之分。它通常以字母E表示，以长度单位计量。

图1-10　射弹散布

图1-11　射弹散布概率偏差(www.xing528.com)

大量的观察表明，射弹落点相对于平均弹着点的坐标为平面上的二维随机变量，且满足正态分布规律。若取坐标轴与散布椭圆的主轴相重合，而坐标原点任选，则落点坐标（x，z）有如下分布规律：

式中　ρ——常数（ρ=0.477）；

Ex——坐标x的中间偏差，通常被称为射弹的距离（或射程）的概率偏差；

Ez——坐标z的中间偏差，通常被称为方向（或侧向）的概率偏差；

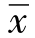和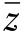——平均弹着点的x和z的坐标，而且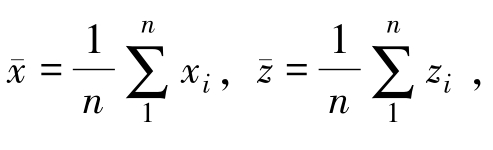n为射弹发数。

Ex，Ez与均方差之间有如下关系：

同理，在坐标y的方向上，有高低概率偏差：

式中　平均弹着点坐标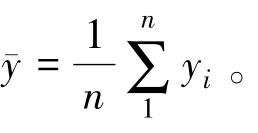

在实际中就是利用射弹散布概率偏差Ex、Ey和Ez的大小来衡量射击密集度的好坏。一般来说，如果弹药的射程为X，则对水平面上的目标进行射击，用距离概率偏差Ex和方向概率偏差Ez，或用相对概率偏差Ex/X和Ez/X表征射击密集度；对垂直目标射击，用高低概率偏差Ey和方向概率偏差Ez，或用相对概率偏差Ey/X和Ez/X表征射击密集度；对空中目标进行射击，用距离概率偏差Ex、高低概率偏差Ey和方向概率偏差Ez，或用斜距离概率偏差ED、法向概率偏差En表征炸点散布。对不同的国家或不同的武器来说，表示射弹散布或射击密集度的方法各有不同。

散布密集界：散布密集界，为在射弹散布面上包含70%弹着点、对称且平行于散布轴的两条平行线间的区域，如图1-12所示。其宽度常用字母C表示，约为全散布宽度的1/3，也有方向、高低和距离散布密集界之分。弹着平面上相互垂直的两个散布密集界交叉而形成的矩形被称为中央半数必中界，其中约包含全部弹着点的50%。理论分析证明C=3.07E。可以概略地认为C=3E。

散布圆半径或圆概率偏差（CEP）：散布圆半径，常用于射弹较少或散布区域近于圆形的射击，如步枪、机枪对300 m以内目标的射击，或远距离地地导弹的射击。以平均弹着点为圆心，包含全部弹着点50%的散布圆的半径R50被称为圆概率偏差，亦称半数必中圆半径；包含全部弹着点100%的散布圆半径R100被称为全散布圆半径，如图1-13所示。在理论上R100是无限大的，并不存在，故实际应用中常将包含全部弹着点98.7%～99.8%的散布圆近似作为全散布圆。理论分析可以证明R50=1.75E，R100=（2.5～3）R50。

图1-12　垂直散布面上的散布密集界

图1-13　圆形散布面上的散布圆半径

射击精度都是由实际射击结合理论计算来确定的。提高弹药的射击精度，主要依靠采用先进的技术设备（如制导系统、火控系统等），改进武器弹药设计，保证制造质量，加强武器系统的维护保养，提高射表精度，减小外界因素（如气温、风、能见度、波浪、海流等）影响，以及提高指挥员和射手的射击训练水平等来实现。