如何辅助计算数控加工的切削数据？

编程人员在拿到图纸进行编程时，首先要作必要的工艺分析处理，并在零件图上选择编程原点，建立编程坐标系。从理论上讲，编程原点可以任意选取。编程时，在保证加工要求的前提下，总希望选择的原点有利于简化编程加工，尽可能实现直接利用图纸尺寸数据编程，以减少数据计算。

实际生产中，当编程原点选定并据此建立编程坐标系后，为了编程并实现优化加工，往往还需要对图纸上的一些标注尺寸进行适当的转换或计算。通常包括以下内容。

1.尺寸换算

如图2-23 所示零件，经分析后将编程原点定在其右端面与轴线交点处。如果采用绝对坐标编程，则端面A、B 的坐标数据需要计算。对于端面B 由于是未注公差，可以直接采用公称尺寸进行计算。而端面A 的向坐标，需要应用工艺尺寸链进行解算。根据尺寸链计算公式得

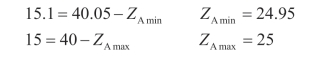
2.公差转换

零件图的工作表面或配合表面一般都注有公差，公差带位置各不相同。图2-22 中，有7个尺寸注有公差要求，其公差带均为单向偏置。数控加工与传统加工一样存在诸多的误差影响因素，总会产生一定的加工误差。如果按零件图纸公称尺寸进行编程，加工后的零件尺寸将出现两种情况：一种大于公称尺寸；另一种小于公称尺寸。从理论上讲，两种情况出现的概率各为50%。对于公差带单向偏置的尺寸，如果按公称值进行编程加工，将会意味着50%的不合格可能性，其中一部分已经是废品（如外圆尺寸小于下偏差），而另一部分还可以通过补充加工进行修正（如外圆尺寸大于上偏差）。上述两种情况的出现都将带来不必要的经济损失。

基于上述原因，数控编程时通常需将公差尺寸进行转换，使其公差带成对称偏置，再以此尺寸公称值编程，从而最大限度地减少不合格品的产生，提高数控加工效率和经济效益。(www.xing528.com)

图2-22 中零件经上述各项换算转换后即形成图2-23 所示零件，编程时使用该图所注尺寸的公称数据即可。

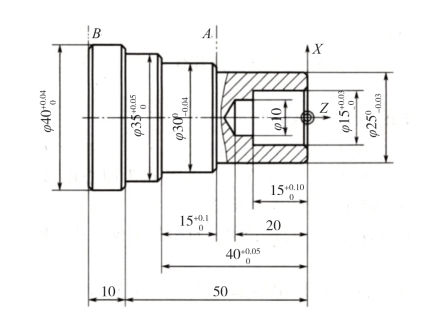
图2-22　零件原图

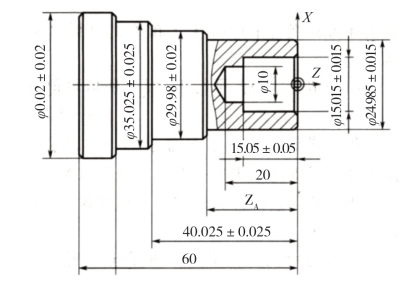
图2-23　零件转换等效图

3.粗加工及辅助程序段路径数据计算

数控加工与传统加工一样，一般不可能一次走刀将零件所有余量切除，通常需要分粗、精加工多次走刀，以逐步切除余量并提高精度，当余量较大时就要增加走刀次数。手工编程时需要得到走刀路线上各步间连接点的坐标信息，因此当按照工艺要求规划好刀具路线后，尚需求出走刀路线上各相关点的坐标信息，包括程序开始的切入路线相关点与程序结束的切出路线相关点的坐标信息。对于粗加工走刀路线上的坐标信息，一般不需要太高的精度，为了方便计算，通常可利用一些已知特征点做一些必要的简化处理。