一种近似的非线性求解是将载荷分为一系列的载荷增量,可以在多个载荷步内或在一个载荷步的多个子步内施加载荷增量。完成每个增量的求解后,继续下一个载荷增量之前,程序调整刚度矩阵以反映结构刚度的非线性变化。遗憾的是,纯粹的增量近似不可避免地随着每个载荷增量积累误差,从而导致结果最终失去平衡,如图8-229a所示。
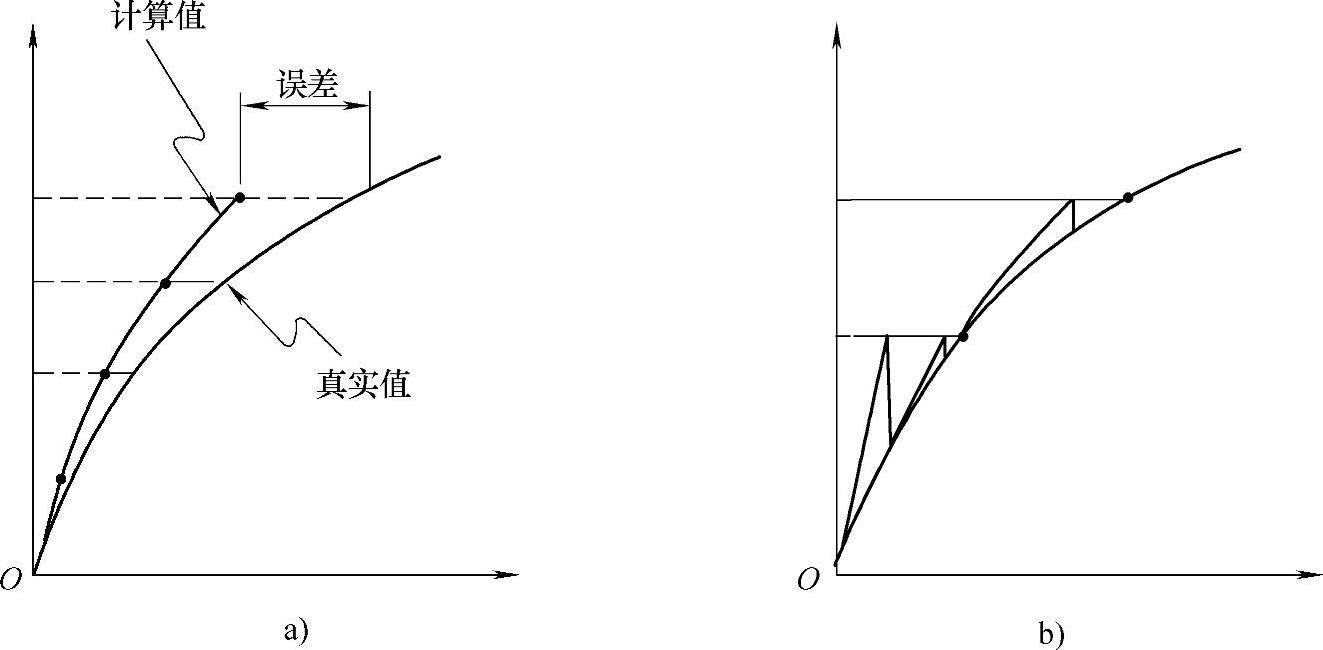
图8-229 平衡迭代
a)纯粹增量式解 b)牛顿-拉普森迭代求解(2个载荷增量)
ANSYS通过使用牛顿-拉普森平衡迭代克服了这种困难,它迫使在每个载荷增量的末端解达到平衡收敛(在某个容限范围内)。图8-229b所示为在单自由度非线性分析中牛顿-拉普森(NR)平衡迭代的使用。在每次求解前,NR方法估算出残差向量,这个向量是回复力(对应于单元应力的载荷)和所加载荷的差值。然后使用非平衡载荷进行线性求解,且核查收敛性。如果不满足收敛准则,重新估算非平衡载荷,并修改刚度矩阵获得新解,持续这种迭代过程直到问题收敛。(https://www.xing528.com)
ANSYS提供了一系列命令来增强问题的收敛性,如自适应下降、线性搜索、自动载荷步及二分等,可被激活来加强问题的收敛性。如果不能得到收敛,那么程序或继续计算下一个载荷或终止。
对某些物理意义上不稳定系统的非线性静态分析,如果仅仅使用NR方法,正切刚度矩阵可能变为降秩矩阵,从而导致严重的收敛问题。这样的情况包括独立实体从固定表面分离的静态接触分析,结构或完全崩溃或突然变成另一个稳定形状的非线性弯曲问题。
对这样的情况,可以激活另外一种迭代方法,即弧长方法帮助稳定求解。该方法导致NR平衡迭代沿一段弧收敛,从而即使当正切刚度矩阵的倾斜为零或负值时,也往往阻止发散。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




