塑性力学问题的研究及应用

在固体力学问题中，当应变比较小时，应力应变关系是线弹性的；当应变比较大时，应力应变关系往往不再是线弹性的，这类问题属于塑性力学范畴。有限元法在这方面的应用是很成功的。

1.单向受力的应力-应变关系

根据金属材料的拉伸试验，受力超过屈服极限以后，材料又恢复了抵抗变形的能力，必须增加载荷，才能继续产生变形，这种现象称为材料的强化（或硬化）。载荷达到最高点时的应力，称为强度极限。

为便于研究，在试验资料的基础上，常抽象为一些简化的模型，如图7-9所示为几种材料的简化模型。其中，1为理想弹塑性模型；2为理想刚塑性模型；3为线性强化弹塑性模型；4为线性强化刚塑性模型。

2.应力张量的分解与应力不变量

在外力作用下，物体内与应力所对应的应变通常分为体积变形和形状变形两部分，这两种变形的变化规律是不同的，对金属而言，在各向均匀压力（或称静水压力）作用下，体积变形是弹性的，不产生塑性变形。为了研究塑性变形必须把各向均匀的压力分离出来，对应的张量做出分解后，可得到应力球张量和应力偏张量。对金属来说，进入塑性状态后，其体积变形由球张量引起，而与形状改变有关的塑性变形则是由应力偏张量引起的。

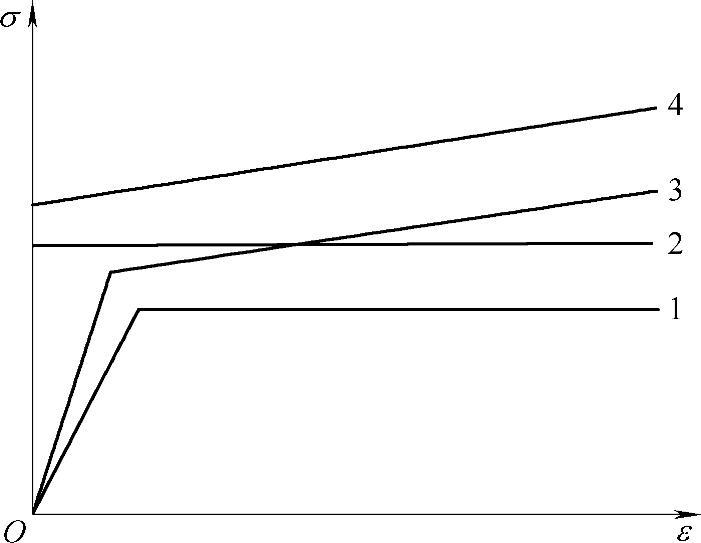
图7-9 几种材料的简化模型

应力球张量和应力偏张量均有三个不变量。

3.屈服准则

理想弹塑性模型在单向受力时，当应力小于屈服极限σ_s时，材料处于弹性状态。当应力达到σ_s时，材料即进入塑性状态。因此，σ=σ_s就是单向受力时的屈服条件。

在复杂应力状态下，物体内某一点开始产生塑性变形时，应力也必须满足一定的条件，它就是复杂应力状态下的屈服条件。一般来说，它应是六个应力分量的函数，可表示如下

F（σ_x，σ_y，σ_z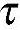，_xy，_yz，_zx）=C （7-7）

式中，C为与材料有关的常数；F为屈服函数。

把某点的六个应力分量代入式（7-7）。如果F＜C，表明该点处于弹性状态；如果F=C，则表明该点处于塑性状态。

考虑的材料是各向同性的，坐标方向的改变对屈服条件没有影响，因此可用主应力表示为

F（σ₁，σ₂，σ₃）=C （7-8）

也可用应力张量不变量I₁、I₂、I₃，或应力偏量不变量J₂、J₃来表示。

屈服条件通常称为屈服准则。

（1）特雷斯卡（Tresca）屈服准则 1864年由Tresca提出：当最大切应力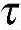_max达到某一定值K时，材料就发生屈服。此条件可表示为

[（σ₁-σ₂）²-4k²][（σ₂-σ₃）²-4k²][（σ₃-σ₁）²-4k²]=0 （7-9）

式中，常数k是由单向拉伸试验确定的，所以k=σ_s/2。如果常数是由纯剪切试验确定的，则k=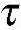_s，其中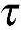_s为纯剪切时的屈服极限。按照Tresca屈服条件，材料的剪切屈服极限与拉伸屈服极限之间存在如下关系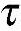

s=σ_s/2 （7-10）

Tresca屈服条件是主应力的线性函数，应用比较方便，它与金属材料的试验资料也基本吻合。但它忽略了中间主应力的影响，且屈服线上有角点，给数学处理带来了一定困难，这是其不足之处。

图7-10所示为Tresca和Mises两种屈服面的形状。(www.xing528.com)

（2）米泽斯（Mises）屈服准则 由Mi-ses于1913年提出的屈服条件，在偏量平面上的屈服线是Tresca六边形的外接圆。主应力空间中过原点并与坐标轴成等角的直线为静水应力轴。过原点并与静水应力轴垂直的平面为π平面。与π平面平行的平面为偏量平面。如图7-10所示，屈服面Mises在偏量平面上是一个六边形的外接圆，在坐标轴平面上是椭圆。其表达式为

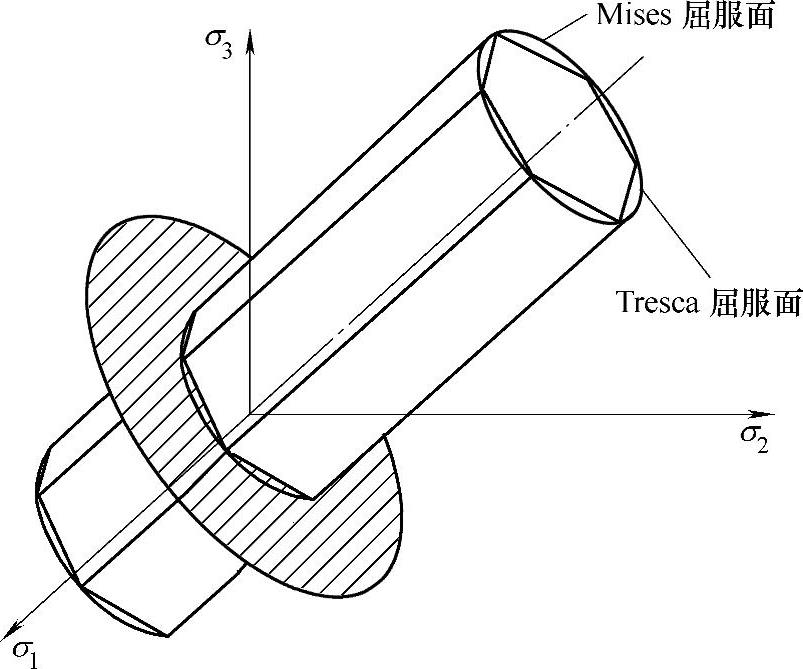
图7-10 Tresca和Mises两种屈服面的形状

它表明，只要应力偏量的第二不变量达到某一定值时，材料就屈服。σ_s是单向拉伸时的屈服极限。

在纯剪切的情况下

J₂=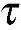_xy=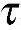²_s=k² （7-12）

由此可见，按照Mises屈服条件，材料的剪切屈服极限_s与拉伸屈服极限σ_s之间的关系为

Mises屈服准则弥补了Tresca屈服准则的不足，更接近实验结果。Mises屈服准则对金属材料比较吻合。

（3）德鲁克-普拉格（Drucker-Prager）屈服准则 对基层、垫层和土地基等弹塑性体积较大的变形材料，莫尔-库仑（Mohr-Coulomb）的强度理论为最早提出的屈服准则。土基、路面等的形变中采用德鲁克-普拉格准则是比较简明的。这里不作阐述。

此外，还有许多其他屈服准则，在此不赘述。

4.强化条件

图7-11所示为单向受力时材料的强化塑性规律变化示意图。在单向受力时，当材料中应力超过初始屈服点A而进入塑性状态后卸载，此后再加载，应力-应变关系将仍按弹性规律变化，直至卸载前所达到的最高应力点B，然后材料再次进入塑性状态。应力点B是材料在经历了塑性变形后的新屈服点，称为强化点。它是材料在再次加载时，应力-应变关系按弹性还是按塑性规律变化的区分点。

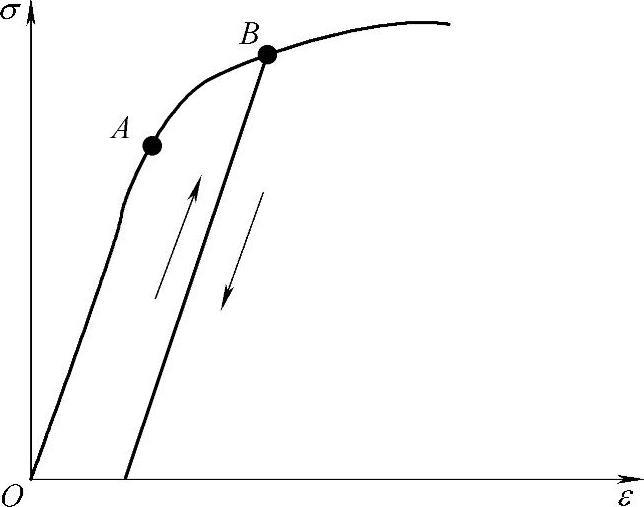
图7-11 单向受力时材料的强化塑性规律

同样，当材料在复杂应力状态下进入塑性后卸载，然后再加载，屈服函数也会随着以前发生过的塑性变形的历史而有所改变。当应力分量满足某一关系时，材料将重新进入塑性状态而产生新的塑性变形，这种现象称为强化。材料在初始屈服以后再进入塑性状态时，应力分量间所必须满足的函数关系，称为强化条件或加载条件，有时也称为后继屈服条件，以区别于初始屈服条件。强化条件在应力空间中的图形称为强化面或加载面。

强化模型主要包括各向同性强化模型、随动强化模型和混合强化模型等。

在以上几种强化模型中，各向同性强化模型使用最为广泛。这一方面是由于它便于进行数学处理；另一方面，如果在加载过程中应力方向（或各应力分量的比值）变化不大，采用各向同性强化模型的计算结果与实际情况也比较符合。随动强化模型可以考虑材料的包兴格（Bauschinger）效应，在循环加载或可能出现反向屈服的问题中，需要采用这种模型。

5.加载与卸载准则

材料达到屈服状态以后，加载和卸载时的应力应变规律不同。单向受力时，只有一个应力分量，由这个应力分量的增加或减小，就可判断是加载还是卸载。对于复杂应力状态，6个应力分量中，各分量可增可减，为了判断是加载还是减载，需要一个准则。

（1）理想塑性材料的加载和卸载 理想塑性材料不发生强化，加载条件和屈服条件相同，应力点不可能位于屈服面外。当应力点保持在屈服面上时，称为加载，因为这时塑性变形可以增长。

设屈服条件为F（σ_ij）=0。当应力达到屈服状态时，F（σ_ij）=0，对于应力增量dσ_ij，如果dF=F（σ_ij+dσ_ij）-F（σ_ij）=0，表示新的应力点仍保持在屈服面上，属于加载。反之，如果dF=F（σ_ij+dσ_ij）-F（σ_ij）＜0，表示应力点从屈服面上退回到屈服面内，属于卸载。

（2）强化材料的加载和卸载 强化材料的加载面可以扩大，因此只有当dσ指向面外时才是加载。当dσ沿着加载面变化时，加载面并不改变，只表示一点的应力状态从一个塑性状态过渡到另一个塑性状态，但不引起新的扭性变形，这种变化过程称为中性变载。dσ指向加载面内时为卸载。