轴对称问题的有限元法求解

如弹性体的几何形状、约束条件及载荷都对称于某一轴，则所有的位移、应力、应变也对称于此轴。这种问题称为对称应力问题，也是在压力容器、机械设计与制造中常见的一类问题。用有限元方法分析轴对称问题时，应将结构离散为有限个圆环单元。圆环单元的截面常用三角形或矩形，也可是其他形式。这种环形单元之间由圆环形铰接，称为结圆。轴对称问题的单元虽然是圆环体，与平面问题的平板单元不同，但由于对称性，可以任取一个子午面进行分析。圆环形单元与子午面上相截生成网格，可以采用平面问题有限元分析相似的方法分析。不同之处是：单元为圆环体，单元之间由结圆铰接，节点力为结圆上的均布力，单元边界为回转面。

对于轴对称问题，采用圆柱坐标（r，θ，z）较为方便。如果以弹性体的对称轴作为z轴，所有应力、应变和位移都与θ无关，只是r和z的函数。任一点只有两个位移分量，即沿r方向的径向位移u和沿z方向的轴向位移w。由于对称，θ方向的环向位移等于零。

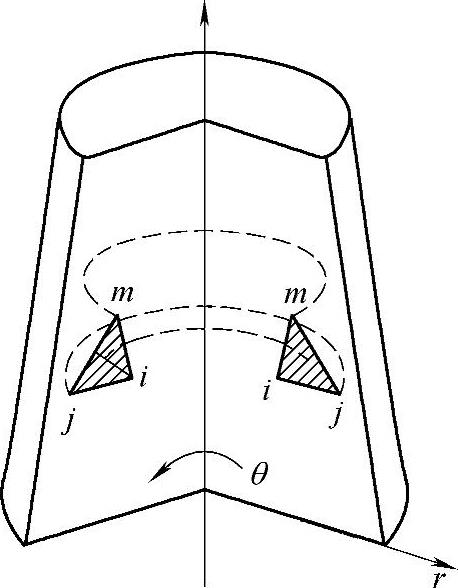
图7-4 圆环和rz平面正交的截面

(www.xing528.com)

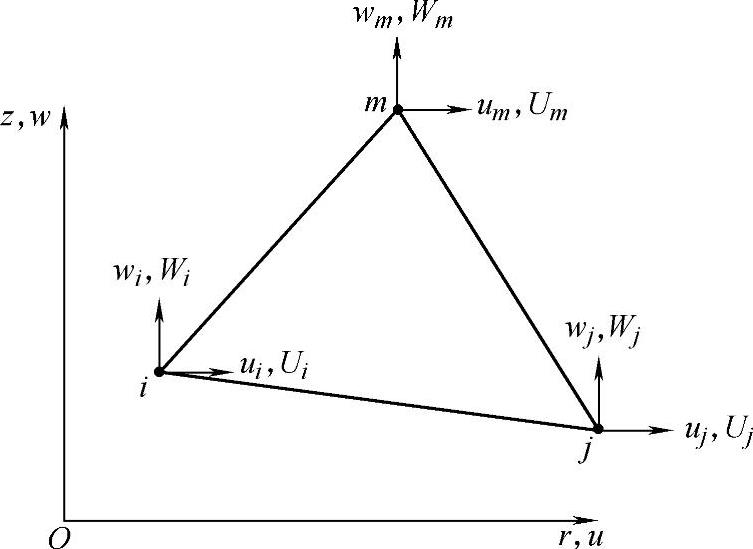
图7-5 三角形网格

在轴对称问题中，采用的单元是一些圆环。这些圆环和rz平面正交的截面通常取为三角形，如图7-4所示的ijm（也可以取为其他形状）。各单元之间用圆环形的铰链互相连接，每一个铰与rz平面的交点称为节点，如i、j、m等。各单元在rz平面上形成三角形网格（图7-5），类似于在平面问题中各三角形单元在xy平面上所形成的网格。但是在轴对称问题中，每个单元的体积都是一个圆环的体积，这点与平面问题是不同的。

假定物体的形状、约束条件及荷载都是轴对称的，这时只需分析一个截面。可以取出环形单元的截面积ijm，如图7-5所示，参照前面章节中的弹簧系统和杆系进行分析，推导其位移函数、单元应变、单元应力、单元刚度矩阵，最后求出节点载荷。这里不再展开。