平面问题有限元模型优化

在第6章中提到，工程中许多构件形状与受力状态可以使它们简化为二维情况处理，这就是弹性力学平面问题。平面问题有两种情况，即平面应力问题和平面应变问题。在弹性力学中，需将系统进行分解与合成。与弹性力学类似，在有限元法中，为便于计算，也是将系统进行离散分割与合成，主要分割注意事项如下：

1）对于杆和连续梁，模型按照原有系统结构自然分割，连接形式也和原系统一致。其计算与结构矩阵匹配。

2）对连续体，要用有限元法进行矩阵分析，就需人为地将连续的平板分割成有限个小块的单元，这就称为结构的离散。

最简单的分割单元为三角形单元和矩形单元，如图7-1所示。多数情况下，人们选择矩形单元进行单元分割。

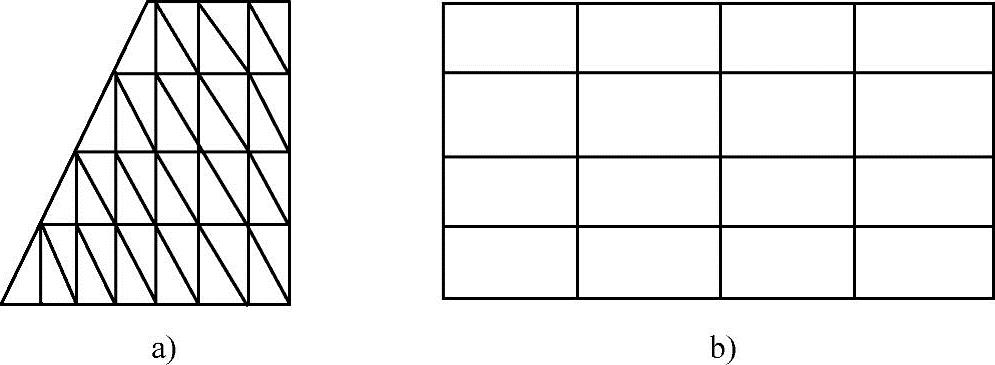
图7-1 分割单元

a）三角形单元 b）矩形单元

接下来就有这样一个问题，原来的连续体被人为分割后，在受到外载荷时，两相邻单元的边界不一定能一起变形。可能出现图7-2所示的情况，即单元间将可能产生裂缝，也就是说离散后的模型必然比原来的结构柔性要大，应该如何解决这个问题呢？在有限元法中，在选择合适的离散分割（后面称为网格划分）后，往往还需选择适当的单元位移插值函数来限制单元的变形，使连续体尽管被人为分割，但模型仍然能够部分（或全部）满足连续性的要求。也就是说，有限元不仅仅是使由原始结构分割而成的一些碎块，而是一些特殊类型的弹性单元，这些弹性单元被限制成特定的模式，以使得单元集合体的整体连续性得以保持。

一般来说连续体的有限元法求解至少有两点不同于刚架结构的有限元分析：第一，连续体的结构必须人为地分割成许多单元；第二，由位移插值函数限制各个单元乃至整个有限元模型变形的情况。

位移插值函数的形式与所分析结构的类型、单元形式和计算结果的精度要求等因素有关。为了随着单元尺寸的减小（单元数目增多），有限元计算结果能收敛于精确解，所选择的位移插值函数必须满足下列三个条件：

1）位移插值函数应能反映单元的刚体位移。

2）位移插值函数应能反映常量应变——常应变准则。

3）位移插值函数应能保证单元内及相邻单元间位移的连续性——变形协调性（相容性）准则。

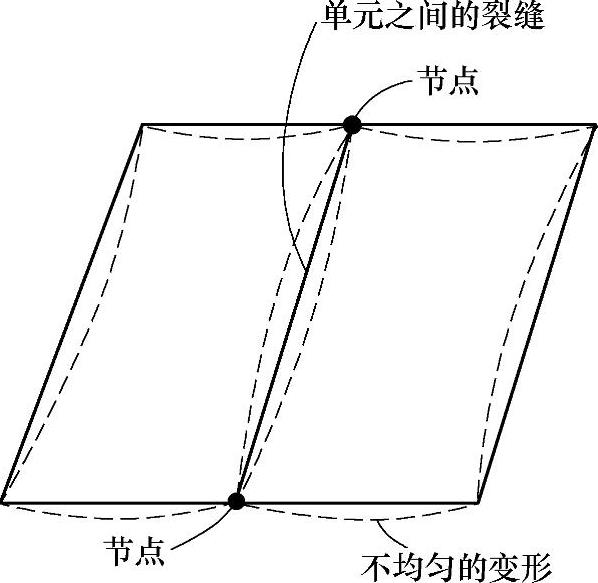
图7-2 单元间产生裂缝

需要指出的是：弹性体的有限元分析中单元分割和位移函数的选择固然至关重要，但对初学者来说，只需要知道其基本概念。因为在众多有限元软件中，一般情况下只需通过选择单元类型即可，而不必知道网格划分后位移函数的具体选择。(www.xing528.com)

对连续体的有限元分割，需要注意如下几点：

1）对给定结构，分割多少单元合适？一般来说，单元分割数目越多，求解精度越高，但会消耗更多计算机资源。

2）单元的分割方式。同一结构中单元之间的大小无限制，可以自由地分布单元，但应在应力集中部位布置较多的单元。

3）单元分割尽量与外载荷匹配。集中力作用点最好布置成节点，而分布载荷则可按照等效原则转化为集中力作用在节点上。如图7-3所示，连续体受到一个均布的压力，而在进行单元分割后，均布载荷就变成了集中载荷作用在表面各个单元的节点上。

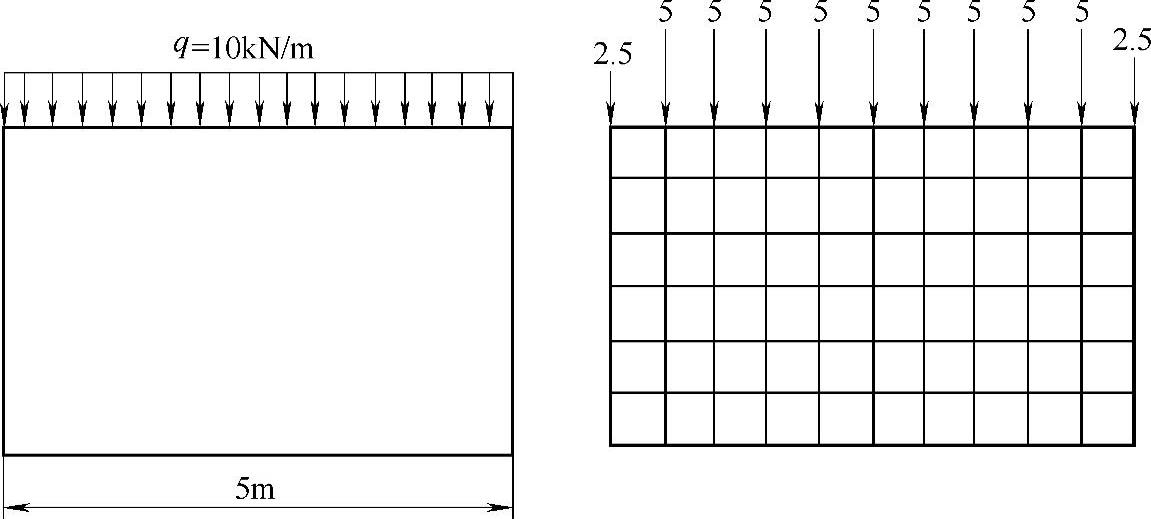
图7-3 均布载荷作用在表面各个单元的节点上

对二维连续体，用有限单元法分析的基本步骤如下：

1）用虚拟的直线把原介质分割成有限个三角形单元，这些直线是单元的边界，几条直线的交点即为节点。

2）假定各单元在节点上互相铰接，节点位移是基本的未知量。

3）选择一个函数，用单元的三个节点的位移唯一地表示单元内部任一点的位移，该函数称为位移函数。

4）通过位移函数，用节点位移唯一地表示单元内任一点的应变；再利用广义胡克定律，用节点位移可唯一表示单元内任一点的应力。

5）利用能量原理找到单元内部应力状态等效的节点力；再利用单元应力与节点位移的关系，建立等效节点力与位移的关系。这是有限元法求解应力问题最重要的一步。

6）将每个单元所受载荷，按照静力等效原则移植到节点上。

7）在每个节点上建立用节点位移表示的静力平衡方程，得到一个线性方程组；解出这个方程组，求出节点位移，然后可以求得每个单元的应力。

总的来说，有限元法的基本思想就是：一分一合，化整为零，集零为整。