弹性力学平面问题的研究与分析

工程中许多构件形状与受力状态可以使它们简化为二维情况处理，这就是弹性力学的平面问题。

弹性力学可分为空间问题和平面问题，严格地说，任何一个弹性体都是空间物体，一般的外力都是空间力系，因而任何实际问题都是空间问题，都必须考虑所有的位移分量、应变分量和应力分量。但是，如果所考虑的弹性体具有特殊的形状，并且承受的是特殊外力，就有可能把空间问题简化为近似的平面问题，只考虑部分的位移分量、应变分量和应力分量即可。这里主要讨论平面问题。

平面问题有两种情况，即平面应力问题和平面应变问题。

如图6-20所示，厚度为t的很薄的均匀木板，只在边缘上受到平行于板面且不沿厚度变化的面力，同时，体力也平行于板面且不沿厚度变化。这类问题就属于平面应力问题。平面应力问题主要研究等厚度薄板状弹性体，受力方向均沿面板方向。

在图6-20所示的薄板中，在不失稳条件下可以认为在厚度方向，即z方向的应力为0，同时沿该方向的切应力为0。这样，应力分量就只有三个。即

（续）

σ_x=σx（x，y），σ_y=σ_y（x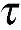，y），_xy=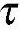_xy（x，y）

平面应变问题处理面内受力但垂直于平面方向上不产生变形的二维受力问题。如图6-21所示为一水坝截面，该截面沿纵向（即z向）很长，且沿横截面不变，受有平行于横截面而且不沿长度变化的面力和体力。由于物体的纵向很长（在力学上可近似地作为无限长考虑），截面尺寸与外力又不沿长度变化；当以任一横截面为xy面，任一纵线为z轴时，则所有一切应力分量、应变分量和位移分量都不沿z方向变化，它们都只是x和y的函数。此外，在这一情况下，由于对称（任一横截面都可以看作对称面），所有各点都只会有x和y方向的位移而不会有z方向的位移。此时u=u（x，y），v=v（x，y），w=0。(www.xing528.com)

因此，这种问题称为平面位移问题，但习惯上常称为平面应变问题。

表1-133 T系列热继电器主要技术性能

表1-134 控制触头额定电压、额定电流及约定发热电流

图6-20 薄板的平面应力

表1-135 继电器动作特性

图6-21 水坝截面的应变问题

根据前面通用的三大方程，同样可以建立平面应力和平面应变的三大物理方程，这里不再赘述。