前面提到,弹性力学三维问题有六个分量,即三个正应力和三个切应力,各个应力向量在图6-18所示的体素中均完整表述出来。下面简单推导弹性力学的三个基本方程。
(1)力学平衡方程 在前微面上在三个方向的应力为
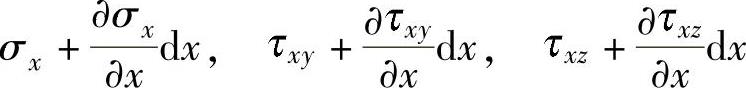
在右微面上沿x、y、z三个方向的应力为
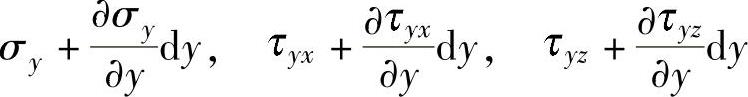
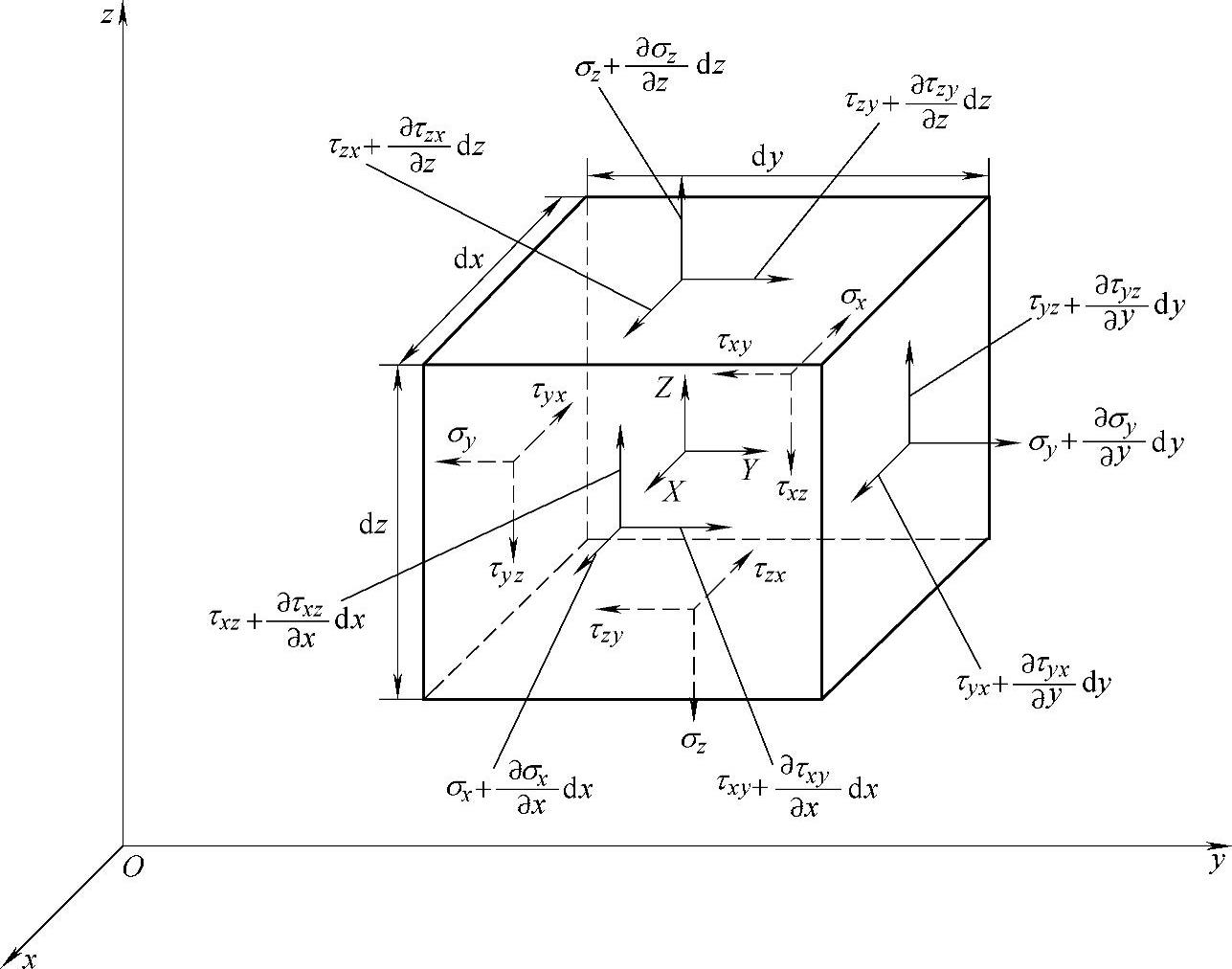
图6-18 体素中的各个应力向量
在上微面上沿x、y、z三个方向的应力为
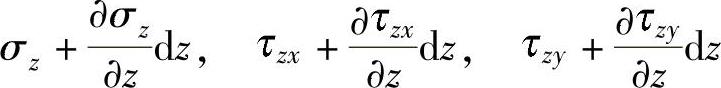
这里,切应力互等定理仍然成立,即
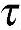 zx=
zx=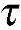 xz,
xz,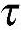 yz=
yz=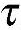 zy,
zy,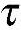 xy=
xy=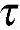 yx
yx
考虑微元体的力平衡条件,在x方向有∑Fx=0,则可得到
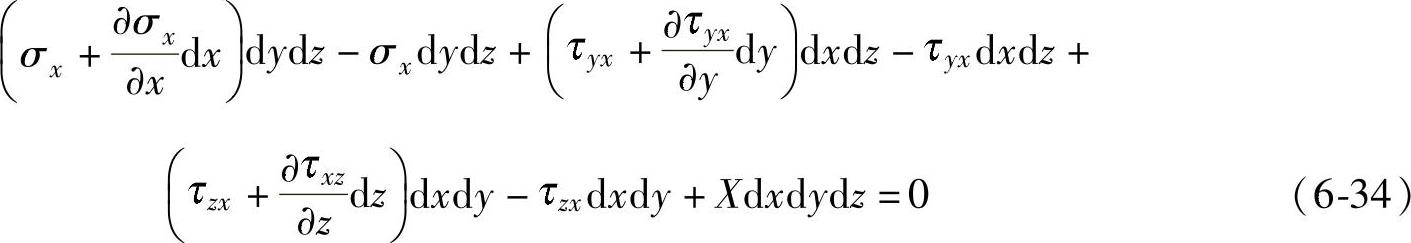
将上式化简后得到

同理,考虑微元体y方向和z方向的力平衡条件,可得到如下方程

式(6-35)、式(6-36)和式(6-37)就构成了弹性力学的力学平衡方程。
(2)几何方程 几何方程是表述弹性体内一点的应变与位移之间关系的方程式。下面来推导弹性体的几何方程。(https://www.xing528.com)
弹性体变形微元在xy平面上的投影如图6-19所示。微四边形单元初始形状为矩形PABC,初始位置位于图示坐标中。受外载荷后,形状和位置均发生变化,如P′A′B′C′所示。P、A、B三点的位移均在图中详细标注出来,PA、PB的角位移分别为α和β。
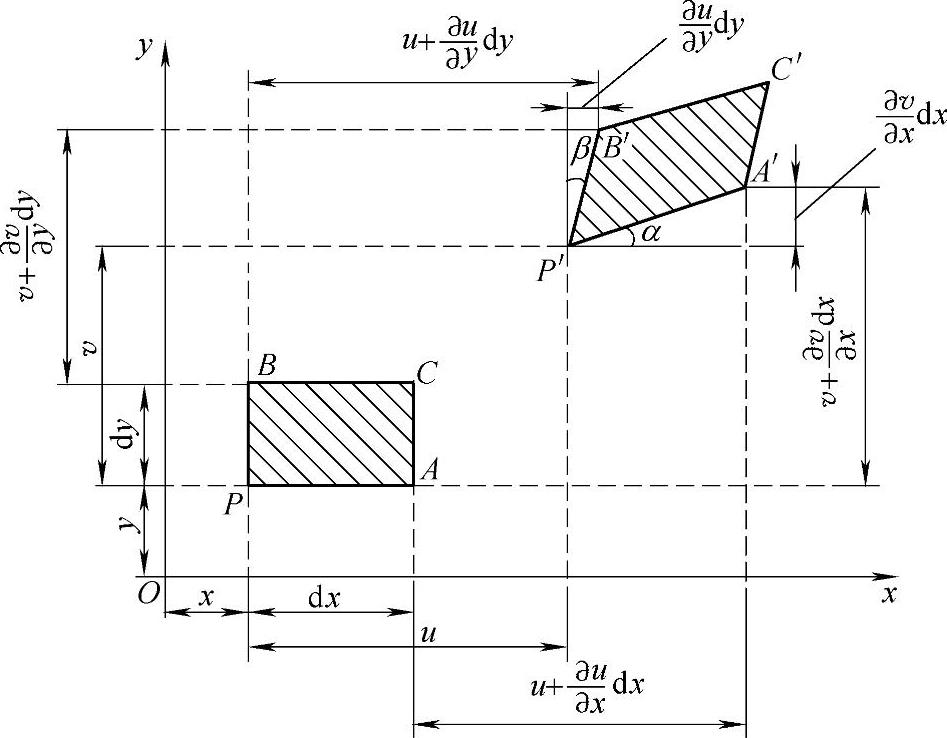
图6-19 弹性体变形微元在xy平面上的投影
由于正应变就是微元体在某方向的长度变化量与原长度之比,由此可以得到两个正应变的公式
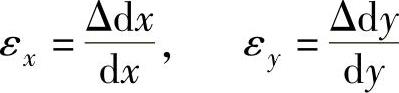
结合图6-18,可以得到
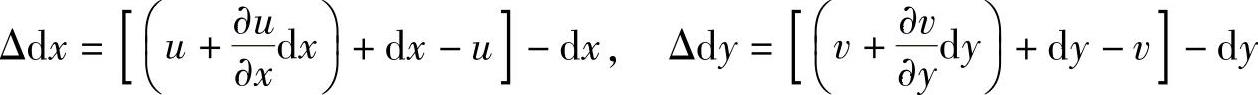
将上述两式代入到定义公式中得到
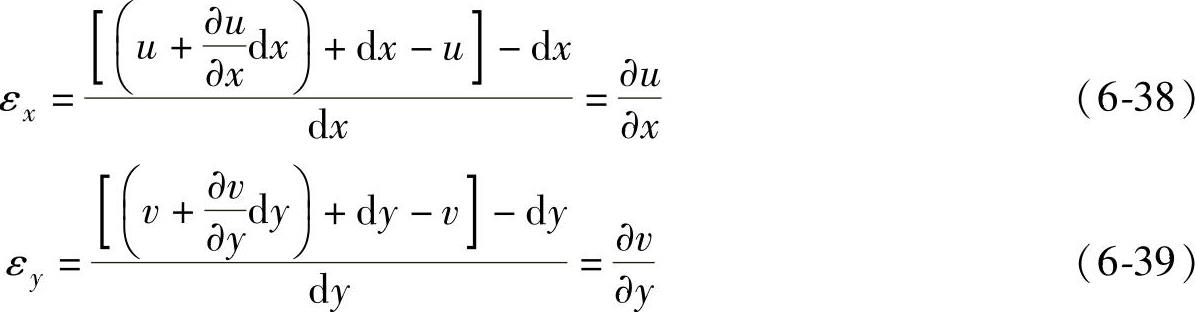
切应变定义为x、y两个方向微元夹角的改变量,则上述微元体的切应变为
yxy=α+β (6-40)
同样,结合图6-18,可以得到微元体切应变的详细推导公式
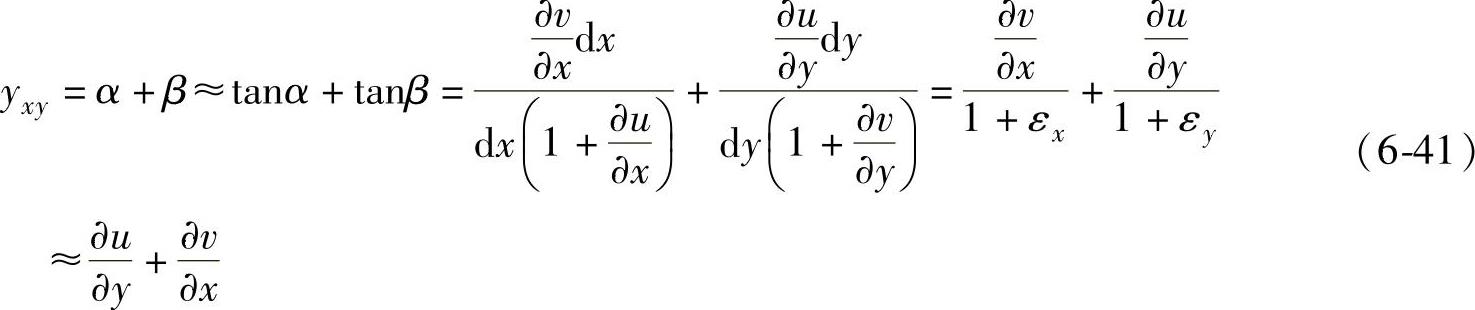
同理,将微元体向其他两个坐标平面投影可得到类似的关系式。这里不再详细推导。于是可以得到x、y和z方向的切应力和切应变,共六个。具体表达如下:
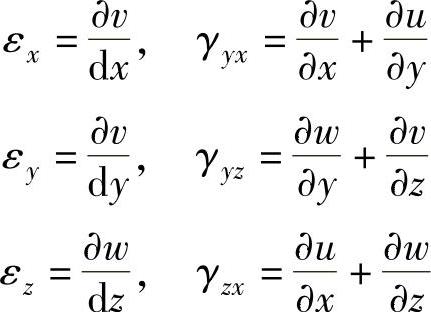
上述方程即为弹性力学的几何方程。
(3)物理方程 物理方程是描述应力与应变关系的方程。在材料力学中用胡克定律描述。而在弹性力学中,由于是三向应力状态,对各向同性的均匀体用广义胡克定律描述。鉴于材料力学中已有推导,这里就直接提出结论。物理方程中,E为弹性模量;μ为泊松比;G为切变模量。
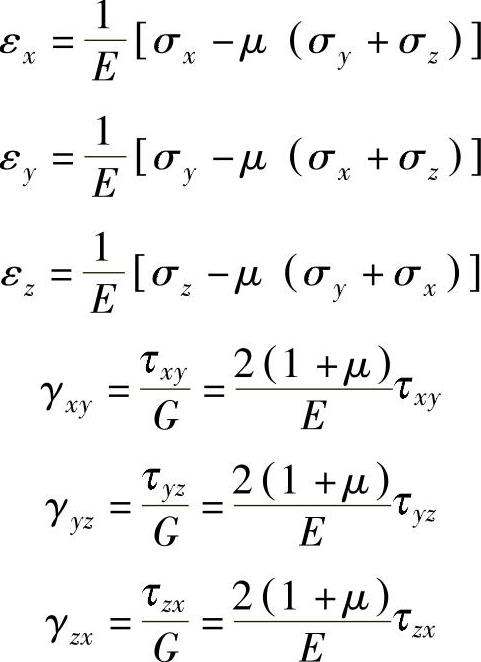
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




