作用于弹性体的外力(或称荷载)可能有两种,即表面力和体力。
表面力是分布于物体表面的力,如静水压力、一物体与另一物体之间的接触压力等。单位面积上的表面力通常分解为平行于坐标轴的三个成分,用记号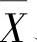 、
、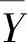 、
、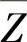 来表示。
来表示。
体力是分布于物体体积内的外力,如重力、磁力、惯性力等。单位体积内的体力也可分解为三个成分,用记号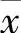 、
、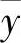 、
、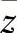 表示。
表示。
弹性体受外力(包括表面力和体力)以后,其内部将产生应力。应力是应重点掌握的概念,下面加以详细阐述。
弹性力学的基本理论是将弹性体分成无穷个微小单元体。这个单元体可以是六面体,也可是四面体,一般以六面体居多。这里假设从弹性体内取一个微小的平行六面体PABC,如图6-16所示,将其称为体素。
在体素中,假设PA=dx,PB=dy,PC=dz。每一个面上的应力分解为一个正应力σ和两个切应力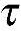 ,分别与三个坐标轴平行。
,分别与三个坐标轴平行。
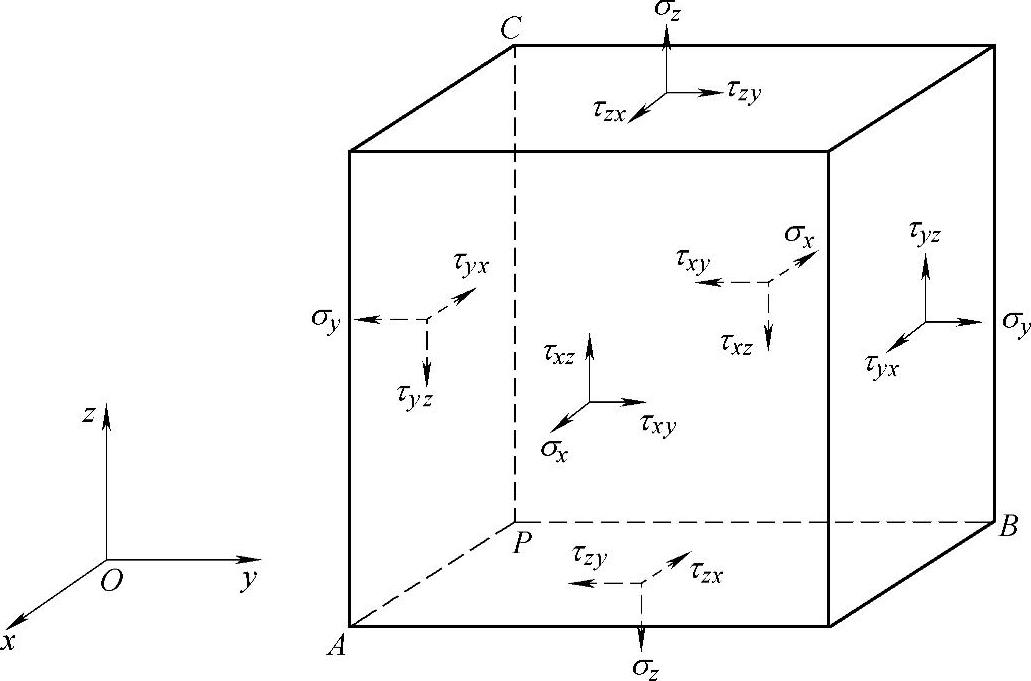
图6-16 体素
(1)正应力σ 为了表明这个正应力的作用面和作用方向,加上一个角码。例如,正应力σx是作用在垂直于x轴的面上同时也沿着x轴方向。
(2)切应力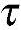 加上两个角码,前一个角码表明作用面垂直于哪一个坐标轴,后一个角码表明作用方向沿着哪一个坐标轴。例如,切应力
加上两个角码,前一个角码表明作用面垂直于哪一个坐标轴,后一个角码表明作用方向沿着哪一个坐标轴。例如,切应力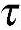 xy是作用在垂直于x轴的面上而沿着y轴方向作用的。(https://www.xing528.com)
xy是作用在垂直于x轴的面上而沿着y轴方向作用的。(https://www.xing528.com)
(3)应力的正负 如果某一个面上的外法线是沿着坐标轴的正方向,这个面上的应力就以沿坐标轴正方向为正,沿坐标轴负方向为负。相反,如果某一个面上的外法线是沿着坐标轴的负方向,这个面上的应力就以沿坐标轴的负方向为正,沿坐标轴正方向为负。
(4)切应力互等定律 作用在两个互相垂直的面上并且垂直于该两面交线的切应力是互等的(大小相等,正负号也相同)。因此切应力记号的两个角码可以对调。例如,在图6-16所示的体素中,由力矩平衡得出
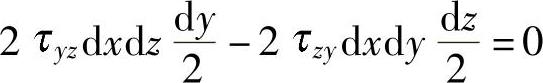
简化得到 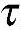 xy=
xy=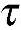 yx
yx
同样可得: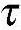 xz=
xz=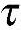 zx,
zx,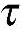 zy=
zy=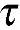 yz,此即切应力互等定律。
yz,此即切应力互等定律。
从图6-16所示的体素中可以明显看出,弹性力学三维问题有六个分量,即三个正应力σx、σy和σz,三个切应力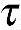 xy、
xy、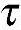 yz和
yz和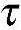 zx。可以证明:如果这六个量在P点是已知的,就可以求得经过该点的任何面上的正应力和切应力,因此,这六个量可以完全确定该点的应力状态,它们就称为在该点的应力分量。
zx。可以证明:如果这六个量在P点是已知的,就可以求得经过该点的任何面上的正应力和切应力,因此,这六个量可以完全确定该点的应力状态,它们就称为在该点的应力分量。
一般说来,弹性体内各点的应力状态都不相同,因此,描述弹性体内应力状态的上述六个应力分量并不是常量,而是坐标x、y、z的函数。
六个应力分量的总体,可以用一个列矩阵来表示
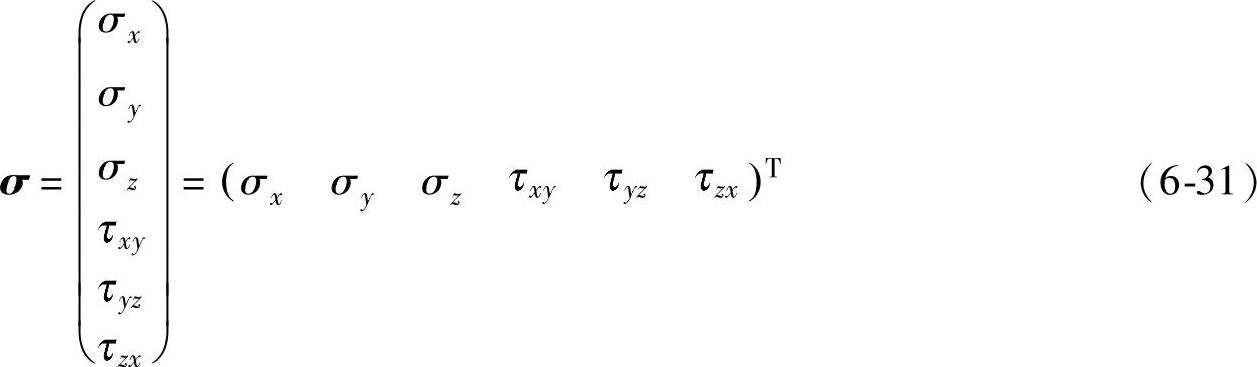
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




