【摘要】:具体而言,包括线性、非线性最小化及最大化,二次规划,半无限问题,线性、非线性方程(组)的求解,线性、非线性的最小二乘问题。另外,该工具箱还提供了线性、非线性最小化,方程求解,曲线拟合,二次规划等问题中大型课题的求解方法,为优化方法在工程中的应用提供了更方便快捷的途径。优化工具箱中常用的求极值函数见表4-2。归纳总结上述函数,得出优化工具箱能求解的优化模型,如图4-11所示。
利用MATLAB的优化工具箱,可以求解线性规划、非线性规划和多目标规划问题。具体而言,包括线性、非线性最小化及最大化,二次规划,半无限问题,线性、非线性方程(组)的求解,线性、非线性的最小二乘问题。另外,该工具箱还提供了线性、非线性最小化,方程求解,曲线拟合,二次规划等问题中大型课题的求解方法,为优化方法在工程中的应用提供了更方便快捷的途径。
优化工具箱中常用的求极值函数见表4-2。
归纳总结上述函数,得出优化工具箱能求解的优化模型,如图4-11所示。
使用优化工具箱时,由于优化函数要求目标函数和约束条件满足一定的格式,所以需要用户在进行模型输入时注意以下几个问题:
1.目标函数最小化
优化函数一般都要求目标函数最小化,如果优化问题要求目标函数最大化,可以通过使该目标函数的负值最小化即-f(X)最小化来实现。
表4-2 优化工具箱中常用的求极值函数(https://www.xing528.com)

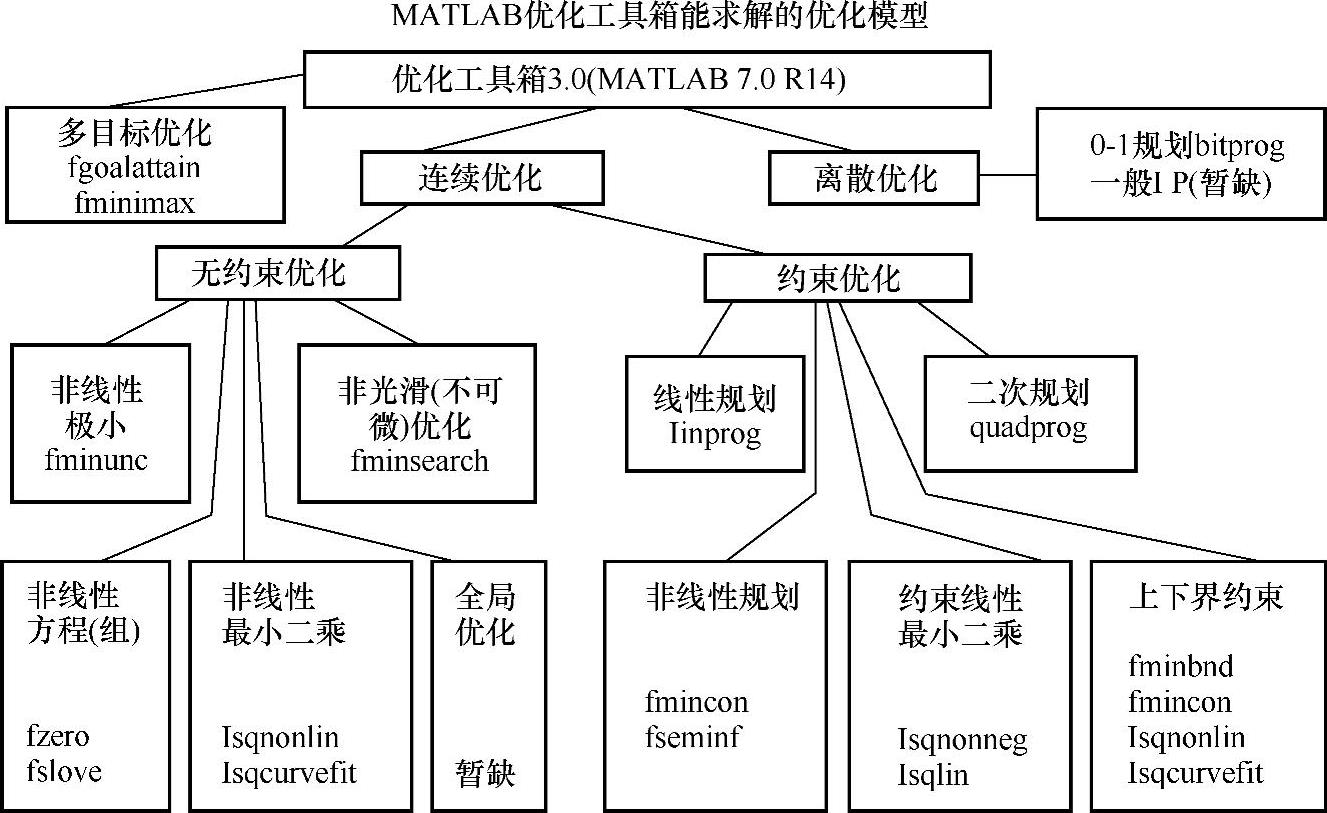
图4-11 优化工具箱能求解的优化模型
2.约束非正
优化工具箱要求非线性不等式约束的形式为Ci(x)≤0,通过对不等式取负可以达到使大于零的约束形式变为小于零的不等式约束形式的目的,如Ci(X)≥0等价于-Ci(X)≥0,Ci(X)≥b形式的约束等价于-Ci(X)+b≥0。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




