圆柱齿轮减速器优化设计探究

例4-3 设计一个单级直齿圆柱齿轮减速器，其输入功率P=280kW，输入转速为n₁=980r/min，传动比i=4，工作寿命要求达到L_h=72000h，大小齿轮材料均为40Cr，调质后表面淬火，[σ_H]=855MPa，[σ_F1]=256MPa，[σ_F2]=210MPa，要求在满足正常工作条件下减速器体积最小。

确定设计变量。设计变量必须是相互独立的一组参数，这里将齿宽、模数和小齿轮齿数作为独立设计参数X=（x₁x₂x₃）^T=（Bmz₁）^T。

要使目标体积最小，可以转化为求减速器的中心距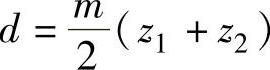最小。故可以得到目标函数为

minf（X）=0.5x₂（x₃+4x₃）=2.5x₂x₃

再根据相关准则建立约束条件如下：

1）小齿轮的齿数应大于不产生根切的最小齿数，一般选取17≤z₁≤25，可得

g₁（X）=17-x₃≤0，g₂（X）=x₃-25≤0

2）齿轮的齿面最大接触应力应不大于[σ_H]，查《机械设计手册》齿轮齿面接触应力相关公式，将数据代入可以得到

g₃（X）=43854x₁^-0.5x₂^-1x₃^-1-855≤0

3）按大小齿轮的弯曲疲劳强度校核，代入相关公式，可得

g₄（X）=7098/[x₁x²₂x₃（0.619+0.006666x₃-0.0000854x²₃）]-256≤0

g₅（X）=7098/[x₁x²₂x₃（0.2824+0.0003539x₃-0.0000015×16x²₃）]-210≤0

4）齿轮宽度应满足

g₆（X）=1.11x₁-x₂x₃≤0

5）齿轮的模数一般选取2mm≤m≤5mm，即

g₇（X）=2-x₂≤0，g₈（X）=x₂-5≤0

综上所述，总结出齿轮减速器的优化数学模型为

minf（X）=2.5x₂x₃

s.t.g₁（X）=17-x₃≤0

g₂（X）=x₃-25≤0

g₃（X）=43854x₁^-0.5x₂^-1x₃^-1-855≤0

g₄（X）=7098/[x₁x²₂x₃（0.619+0.006666x₃-0.0000854x²₃）]-256≤0

g₅（X）=7098/[x₁x²₂x₃（0.2824+0.0003539x₃-0.0000015×16x²₃）]-210≤0(www.xing528.com)

g₆（X）=1.11x₁-x₂x₃≤0

g₇（X）=2-x₂≤0

g₈（X）=x₂-5≤0

选用MATLAB软件中的求非线性约束类问题函数fmincon求解。

首先编写ff.m文件，用来输出非线性约束：

function[c，ceq]=ff1（x）；

c（1）=43854/（x（1）^0.5∗x（2）∗x（3））-855；

c（2）=7098/（x（1）∗x（2）^2∗x（3）∗（0.169+0.006666∗x（3）-0.0000854∗x（3）^2））-256；

c（3）=7098/（x（1）∗x（2）∗^2∗x（3）（0.2824+0.0003539x（3）-0.0000015∗16∗x（3）^2））-210；

c（4）=1.1111∗x（1）-x（2）∗x（3）；

ceq=[]；

在MATLAB命令窗口中调用ff1.m：

A=[0，0，-1；0，0，1；0，-1，0；0，1，0]；

b=[-17；25；-2.5]；

f=inline（‘2.5∗x（2）∗x（3）’，’x’）；

x0=[50，4，18]；

[x，fval]=fmincon（f，x0，A，b，[]，[]，[]，[]，’ff1’）

经运行，得到如下优化结果：

X=（29.9274 2.0000 17.0000）

fval=85.0000

经过计算圆整后可选B=30mm，m=2mm，小齿轮齿数z₁=17。