优化转向车轮理论转角计算方法

转向车轮（一般是前轮）纯滚动、无侧滑的转向要求是

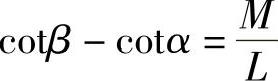
则

式中，α、β为内、外侧转向车轮的理论转角，即内、外侧转向梯形臂的理论转角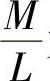；为转向特性参数；M为两转向主销的轴线延长线与地面交点间的距离；L为汽车的轴距。

当内侧转向车轮的实际转角为α时，通过转向梯形所能获得的外侧转向车轮（或转向梯形臂）的实际转角为β′，如图4-2所示。假定转向梯形在过M′的水平平面内运动，不计前轮定位角的影响，不考虑弹性轮胎的侧偏，现以后置转向梯形为例推导β′的函数关系式。

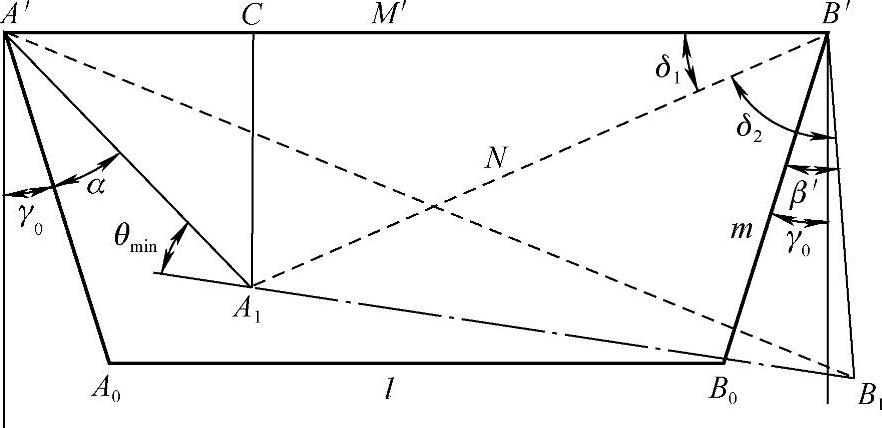
图4-2 转向梯形

图4-2中的梯形A′B′A₀B₀为汽车直线行驶时的位置，而A′B′A₁B₁则是内侧转向梯形臂转过α角时的位置。γ₀为转向梯形的布置角，即直线行驶时，转向梯形臂与车辆纵向平面间的夹角，称为γ₀的余角（90°-γ₀），为梯形底角；m为转向梯形臂过M′水平面的投影长度；M′为连接转向梯形臂处主销轴线间的距离；l为横拉杆长度。则

l=M′-2msinγ₀ （4-3）(www.xing528.com)

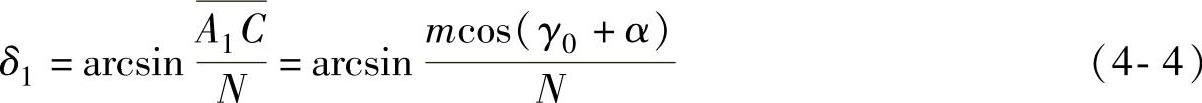
由余弦定理得

N²=M′²+m²-2M′mcos[90°-（γ₀+α）]=M′²+m²-2M′msin（γ₀+α） （4-5）

又 l²=N²+m²-2Nsin（δ₁+γ₀-β′）

则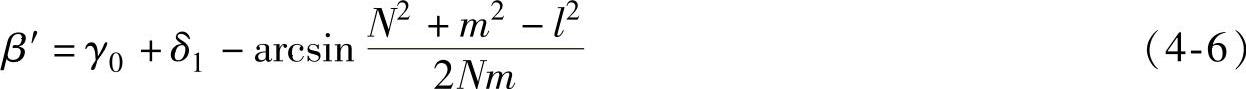

将式（4-2）～式（4-5）代入式（4-6）得

式（4-7）同样适合于前置转向梯形，只是γ₀、α角均要换成负值计算，得出的β′角也为负值。