用统一目标函数法进行优化

统一目标函数法的基本原理是将各分目标函数f₁（X），f₂（X），…，f_p（X）统一到一个新构筑的总的目标函数f（X）=f{f₁（X），f₂（X），…，f_p（X）}中，这样就把原来的多目标问题转化为了单目标问题来求解。根据构筑方法的不同可以分为线性加权组合法、目标规划法和功效系数法。

1.线性加权组合法

线性加权组合法的基本思想是在多目标优化问题中，将其各个分目标函数f₁（X），f₂（X），…，f_p（X）依其数量级和在整体设计中的重要程度相应地给出一组加权因子w₁，w₂，…，w_p，取f_j（X）与w_j（j=1，2，…，p）的线性组合，构成一个新的统一的目标函数，即

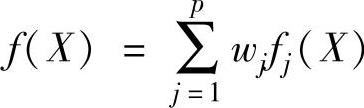
以f（X）作为单目标优化问题求解，即原多目标优化问题转化为求统一目标函数

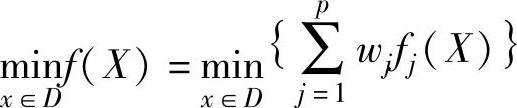
的最优解X^∗，它也是原多目标优化问题的最优解。

上式中，加权因子w_j是一组大于零的数，其取值大小决定于各项目标的数量级及其重要程度。加权因子的选择对计算结果的正确性影响较大，有时要凭经验、凭估计或统计计算并经试算得出。下面介绍一种确定权系数的方法，按此方法

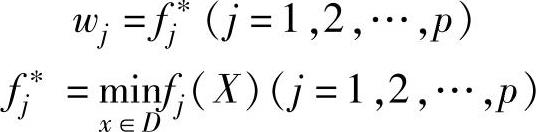
即将各单目标最优化值的倒数取作权系数。此种函数反映了各个单目标函数值离开各自最优值的程度。在确定权系数时，只需预先求出各个单目标最优值，而无需其他信息，使用方便。

2.目标规划法

这种方法的基本思想是为所有目标确定一个预期达到的目标值f_i（X^∗），使作出的优化与该值越接近越好，如完全符合此目标，则是最优解；如不符合，则以离差平方和的大小来衡量其偏离预期值的程度，从而把目标函数f₁（X），f₂（X），…，f_p（X）化为

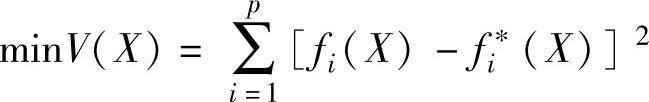
按这种思想还可根据目标的重要程度而采用加权目标的规划法，即

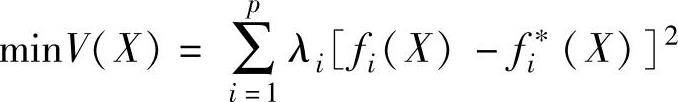
加权系数的确定可参照前面线性加权组合法中权系数的确定方法。

3.功效系数法

每个目标都具有自己所特有的特征。有的目标要求越大越好，如劳动生产率指标；有的要求越小越好，如成本指标；也有要求适中为佳的，如可靠性指标。

为了在评价函数中反映这些不同的要求，可引入功效函数

c_i=F_i（f_i）

c_i的具体数值称为功效系数，它是表示目标满足程度的参数。当c_i=1时，表示对目标最满意；而当c_i=0时，表示对目标最不满意，因此0≤c_i≤1。按上述方法可得出不同目标函数和功效系数之间的变化关系。

当已知目标函数的这种特性曲线以后，对于任一多目标问题，当给定一组X，即可以得到一组相应的c_i，则根据各目标的c_i值构成一评价函数

式中，p是目标函数个数。

当c=1时，所有的目标函数都处在最满意的情况；当c=0时则相反。因此，由不同的X值即可确定不同的c_i值，也得到不同的满意程度，进而反映出目标的不同功效。作为一个综合的目标c，总是要求它越大越好，因此逐步调整变量，可使其达到最大值，进而达到多目标优化的目的。

功效函数值即功效系数，按照对目标函数的不同要求，功效函数可分为以下三种类型：

1）当f_i越大，c_i越大；f_i越小，c_i越小。该类功效函数适合于要求目标函数越大越好。

2）当f_i越小，c_i越大；f_i越大，c_i越小。该类功效函数适合于要求目标函数越小越好。

3）当c_i取的值越靠近预先确定的适当值时，c_i就越大，否则c_i就越小。

功效系数法的关键在于如何确定功效系数c_i。功效系数的确定方法有：直线法、折线法和指数法。

1）直线法。该法需预先定出c_i=1时的f_i和c_i=0时的f_i，在f_i-c_i坐标上将此两点连接后即可求得与f_i对应的c_i值。图3-27a、b、c分别表示采用直线法确定c_i时，对应于上述三种类型的情况。

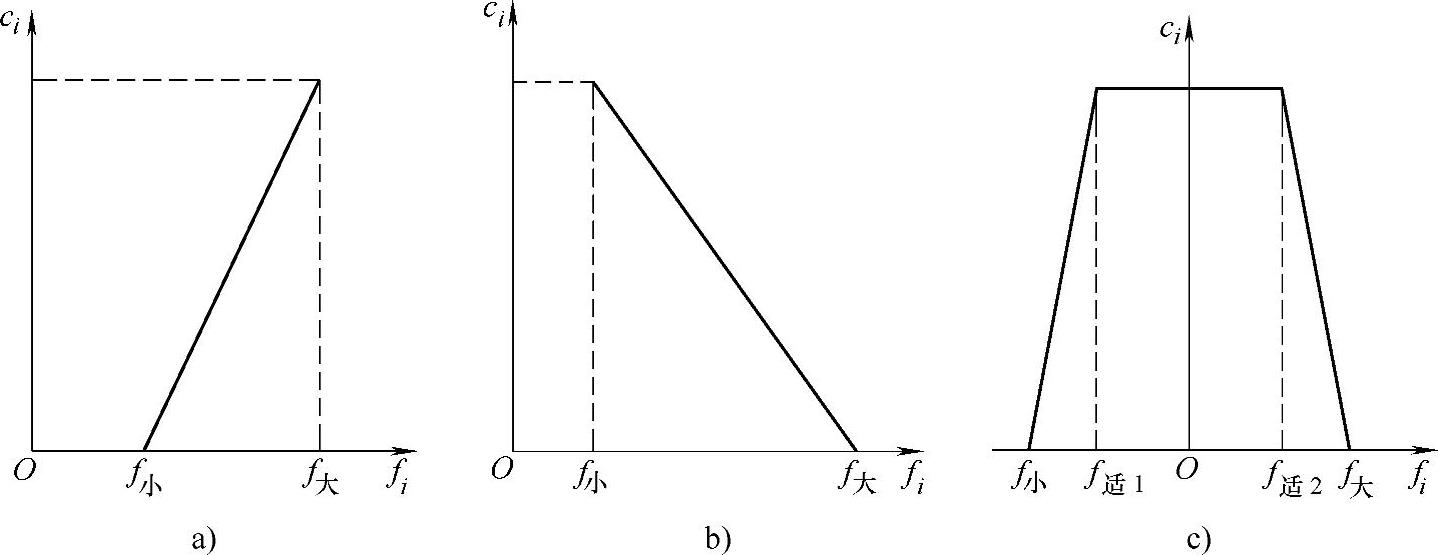
图3-27 用直线法确定ci

2）折线法。该法需要确定f_i的两个临界值f_i^（1）与f_i^（2）。f_i^（1）为比较满意的目标函数值；f_i^（2）为可接受与不可接受的目标函数值的分界值。相应的功效系数如图3-28a、b、c所示。

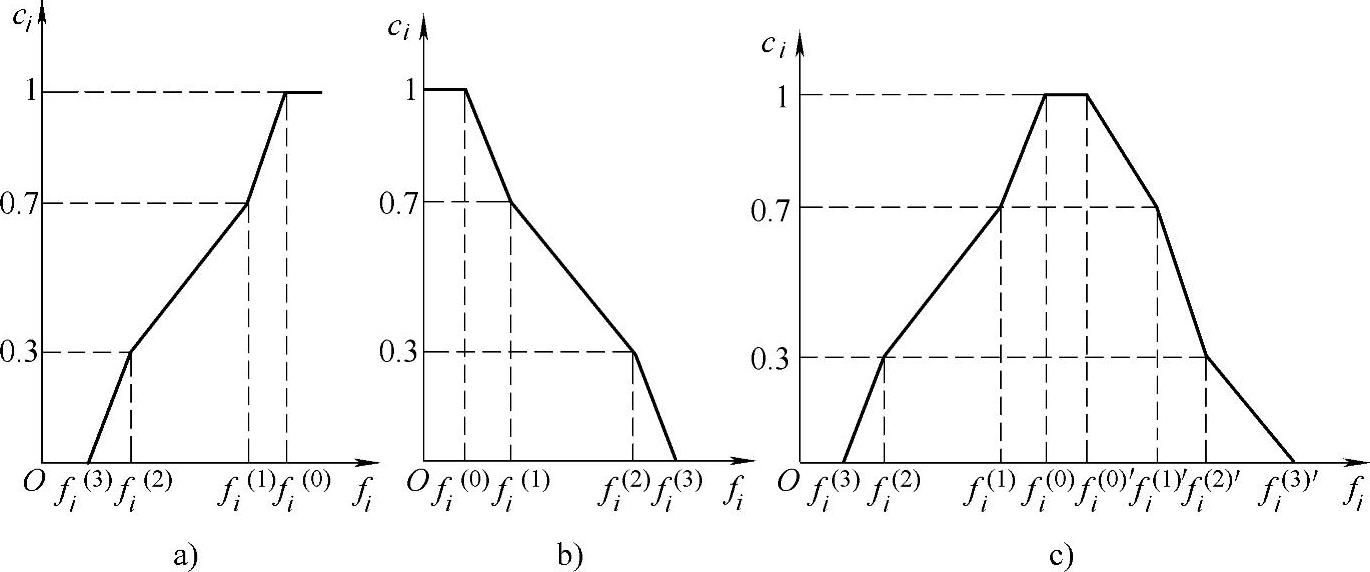
当f_i比f_i^（2）还要差0.5～1倍，即为f_i^（3）时，令c_i=0；当f_i=f_i^（2）时，令c_i=0.3；当f_i=f_i^（1）时，令c_i=0.7；当f_i为理想f_i^（0）时，令c_i=1。

在f_i-c_i坐标上将上述这些特殊点用直线相连，就形成了折线形的功效系数图。当f_i处在f_i^（0）与f_i^（3）之外时，c_i可分别取为1或0。

(www.xing528.com)

图3-28 折线法确定ci

3）指数法。该法对前述第1）类功效函数的选取表达式可表示为

式中，b₀、b₁可以用下法来确定。

设取f为某一刚合格值f^（1）时，c=e^-1≈0.37；f为某一刚不合格值f^（0）时，c=e^-e≈0.07，将上述值代入式（3-21），可解得

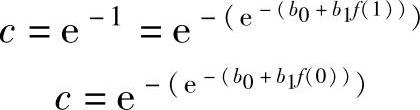
由上面两式可得

b₀+b₁f^（1）=0，b₀+b₁f^（0）=-1

进而可解得

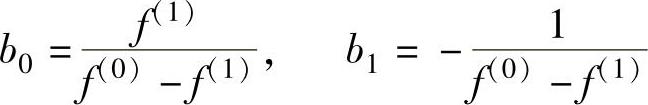
代入式（3-21）可得

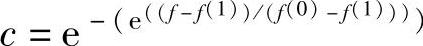
指数法的三类功效函数如图3-29所示。

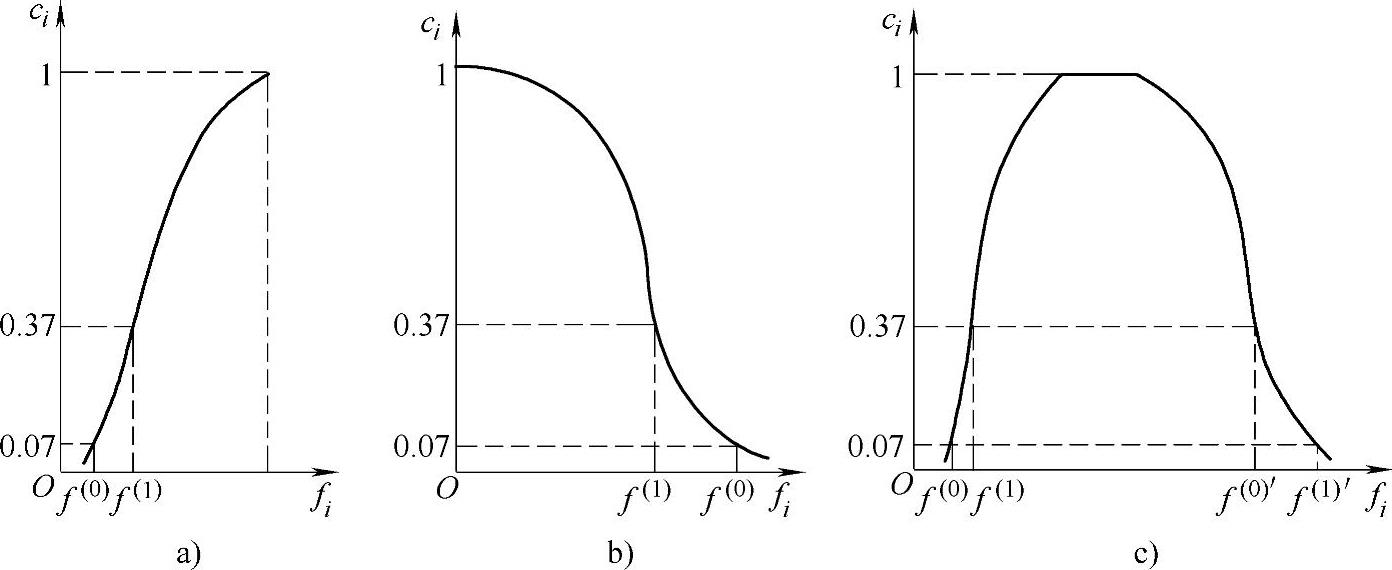
图3-29 指数法确定ci

实践证明，功效系数法有如下优点：

1）可直接按所要求的性能指标来评价函数，非常直观。试算后调整方便。

2）只要有一个性能指标不能接受时，则相应的功效系数c_i为零，从而使评价函数c也为零，方案被否决。这正是实际问题所要求的。它可以避免某一目标函数值不可接受而评价函数值却较好，使优化计算引入歧途。

3）此法还可以处理目标函数值既不希望太大，又不希望太小，而希望取某一适当值的情况。这也是其他优化方法难以对付的一种情况。

该法的缺点是事先要求明确目标函数值的取值范围。对某些问题，若难以确定取值范围时，此法就不适用。

例3-10 设计一曲柄摇杆机构，要求实现摇杆摆角Δψ=60°，最大压力角α_max尽可能小，以改善机构的传力性能；极位夹角θ尽可能大，以提高机构的急回性能。

解 如图3-30所示，设l₁、l₂、l₃、l₄分别为该四杆机构的杆长。

令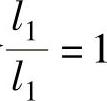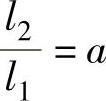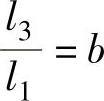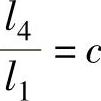，，，，按上述设计要求，可列出该设计的分目标函数分别为

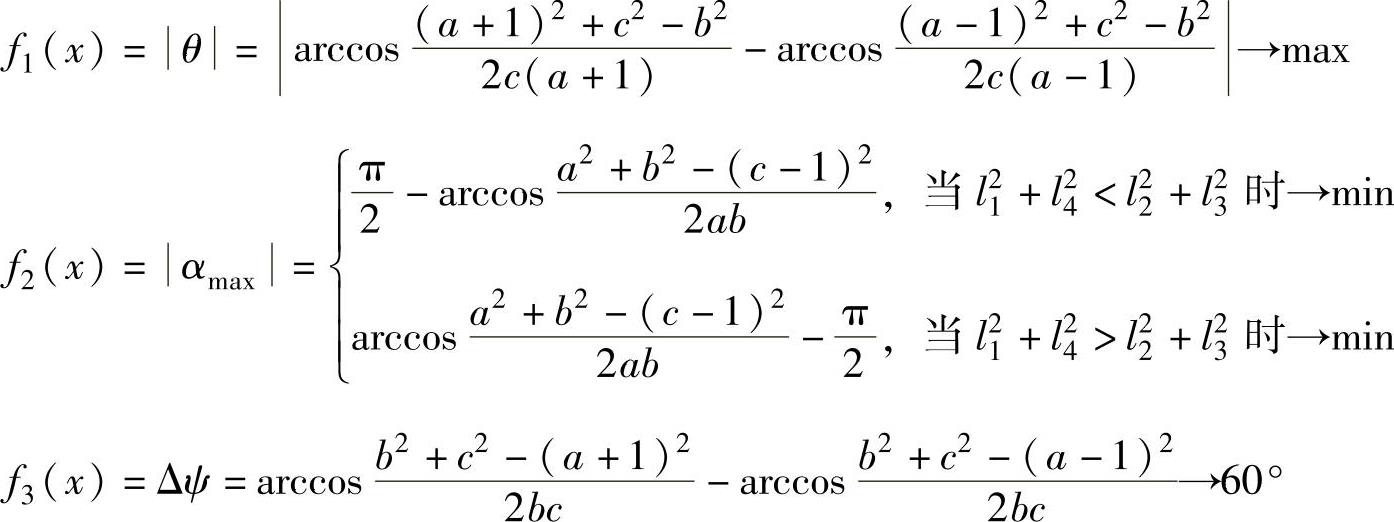
1）f₁（x）为极位夹角，希望越大越好，其取值范围为17°～0°，f₁（x）=17°时，c₁=1；f₁（x）=0°时，c₁=0。

2）f₂（x）为最大压力角，希望越小越好，其取值范围0°～55°，f₂（x）=0°时，c₂=1；f₂（x）=55°时，c₂=0。

3）f₃（x）为摆角，希望越接近60°越好，其取值范围59°～61°，f₃（x）=60°时，c₃=1；f₃（x）=59°时，c₃=0，或f₃（x）=61°时，c₃=0。

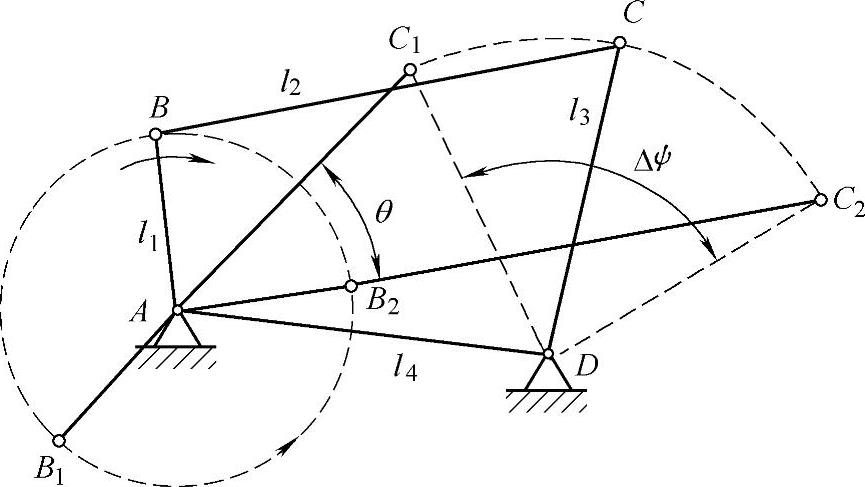
图3-30 曲柄摇杆机构示意图

按上述取值范围，用直线法可作出图3-31所示的功效系数图。代入式（3-20）得该多目标优化问题的评价函数为

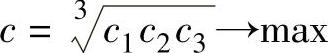
经优化可解出该多目标优化问题的解

当l₁=100mm时，l₂=533.33mm，l₃=200mm，l₄=500mm。

若取l₁=100mm，l₂=352.60mm，l₃=203.62mm，l₄=394.70mm，这时θ=0°，即f₁（x）=0°，此时c₁=0，则c=0，表示此方案不能被接受。

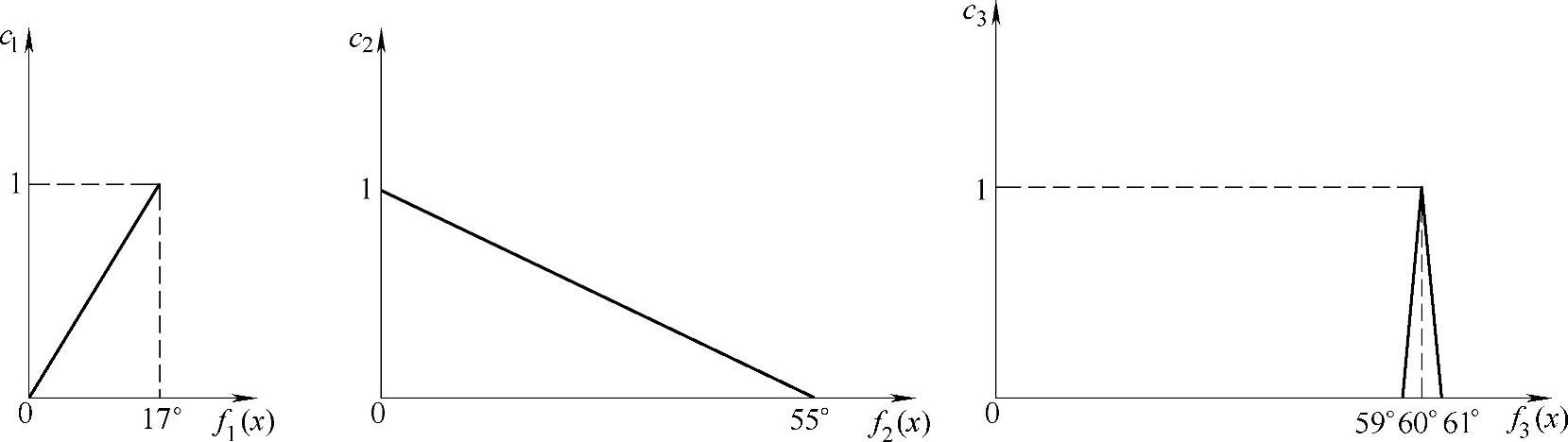
图3-31 直线法功效系数图