内点惩罚函数法：约束优化问题的最优解求解方法

惩罚函数的基本思想是将约束优化问题中的不等式和等式约束函数经过加权转化后，加到原目标函数上，从而形成一个新的目标函数——惩罚函数，即

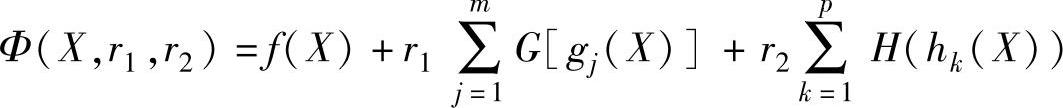
求解该新目标函数的无约束极小值，这样就把原来约束类优化问题转化成了无约束优化问题。式中，r₁、r₂是两个不同的加权因子，通过一定法则不断改变r₁、r₂的值，使新目标函数极小值不断地逼近原约束优化问题的最优解。因此惩罚函数法又可以称为无约束极小化方法，常称SUMT法。

上式中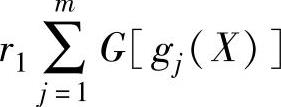，和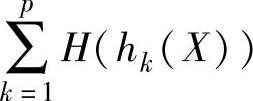称为加权转化项，也称为惩罚项。当设计点X不满足约束条件时，这两项值会增大从而对目标函数形成惩罚。按照惩罚函数在优化过程中迭代点是否在可行域内进行，惩罚函数法又可以分为内点惩罚函数法、外点惩罚函数法、混合惩罚函数法三种。

1.内点惩罚函数法

内点惩罚函数法简称内点法，它的主要特点是将目标函数定义在可行域内，这样，每一迭代点都是在可行域内部移动，从而从可行域内部逐渐逼近原约束优化问题的解，不过内点法只能用来求解具有不等式约束的优化问题。

对于只有不等式约束的优化问题

minf（X），X∈Rⁿ

s.t. g_j（X）≥0 （j=1，2，…，m）

转化后的惩罚函数形式为

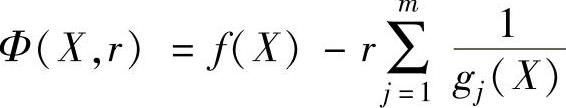
或

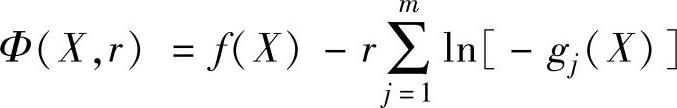
上式中的惩罚因子r是一递减的正数序列，即

r^（0）＞r^（1）＞r^（2）＞…＞r^（k）＞r^（k+1）＞…≥0

对于给定的某一惩罚因子r，当点在可行域内时，两种形式惩罚项的值均大于零，而且当点向约束边界靠近时，两种惩罚项的值迅速增大并趋向无穷。可见，只要初始点取在可行域内，迭代点就不可能越出可行域边界。其次，两种惩罚项的大小也受惩罚因子r的影响。当惩罚因子r逐渐减小并且趋向于零时，对应惩罚项的值也逐渐减小并趋向于零，惩罚函数的值和目标函数的值逐渐接近并趋于相等。当惩罚因子趋于零时，惩罚函数的极小点就是约束优化问题的最优点。内点法的求解过程如图3-25所示，其中最下面的曲线代表目标函数，其他的分别表示几个不同惩罚因子所对应的内点惩罚函数的图形。

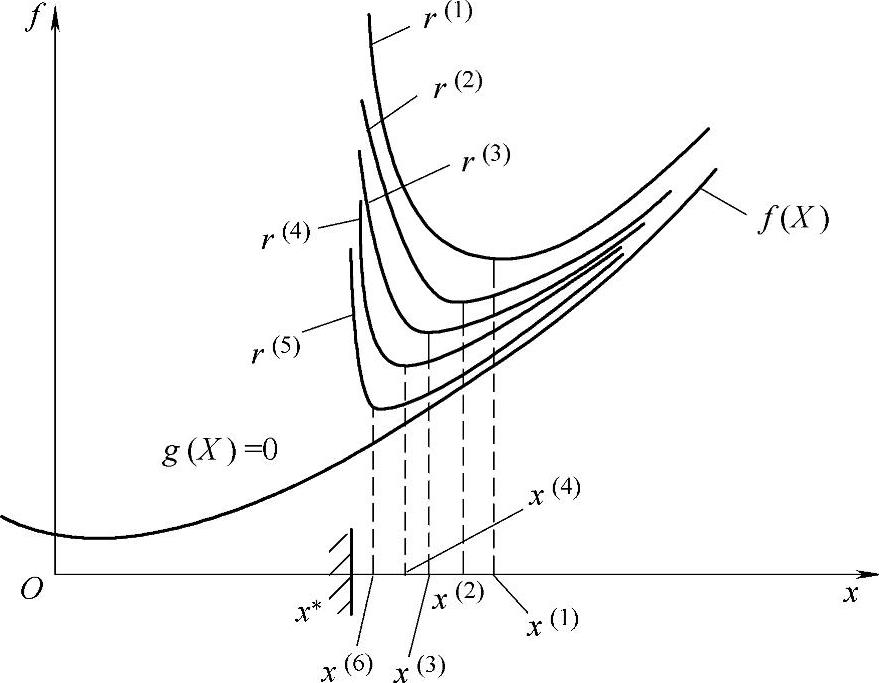
图3-25 内点法的求解过程

在内点法中，初始点X^（0）、惩罚因子的初始值r^（0）及其缩减系数c等参数的选择对计算结果的影响很大，因此这里介绍一下选取这些参数的时候应该注意的一些事项，以及内点法的收敛条件。

1）初始点X^（0）的选择。初始点X^（0）必须是一个满足所有约束条件的点，且最好远离约束边界。当选择可行的初始点有难度时，可先确定各设计变量的上、下限（a_i，b_i），按下式随机选择初始点

X_i^（0）=a_i+r[b_i-a_i] （i=1，2，…，n）

式中，r为[0，1]区间均匀分布的随机数，满足约束条件的一组x即可作为初始点X^（0）。

2）惩罚因子初始值r^（0）和递减系数c的选择。r^（0）的选择对于寻优过程及其结果的影响都很大。r^（0）取值过小，惩罚函数虽然收敛快，但其性能可能变坏，不宜寻优。使用中，可选几个r^（0）试用一下，也可按下式选取

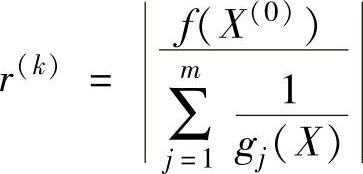
惩罚因子是一个递减数列

r^（k）=cr^（k-1） （k=1，2，…）

通常取c=0.1～0.7之间。

3）内点惩罚函数法的收敛条件为

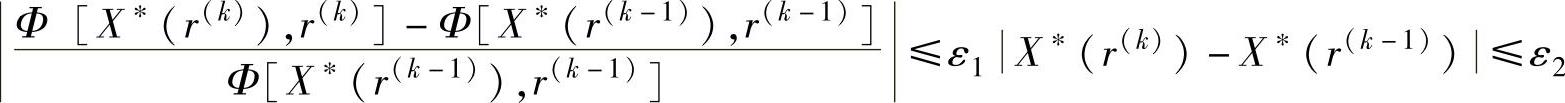
前式说明相邻两次迭代的惩罚函数的值相对变化量充分小，后式说明相邻两次迭代的无约束极小点已充分接近。满足收敛条件的无约束极小点X^∗（r^（k））已逼近原问题的约束最优点，迭代终止。原约束问题的最优解为

X^∗=X^∗（r^（k）），f（X^∗）=f（X^∗（r^（k）））

内点法的计算步骤为：

1）选取可行的初始点X^（0）、惩罚因子的初始值r^（0）、缩减系数c以及收敛精度ε₁、ε₂。令迭代次数k=0。

2）构造惩罚函数Φ（X，r），选择适当的无约束优化方法，求函数Φ（X，r）的无约束极值，得X^∗（r（^k））点。

3）根据收敛条件判别迭代是否收敛，若满足收敛条件，迭代终止。约束最优解为X∗=X∗（r^（k）），f（X^∗）=f（X^∗（r^（k）））；否则令r^（k+1）=cr^（k），X^（0）=X^∗（r^（k）），k=k+1转步骤2）。

例3-8 用内点法求解约束优化问题

minf（X）=x₁+x₂

s.t.g₁（X）=x²₁-x₂≤0

g₂（X）=-x₁≤0

解：构造惩罚函数

minΦ（X，r^（k））=x₁+x₂-r^（k）[ln（-x²₁+x₂）+ln（x₁）]

用极值条件求解，令

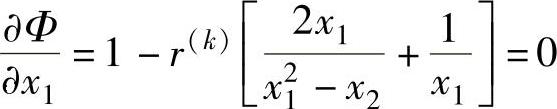
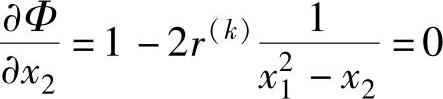
联立求解，得

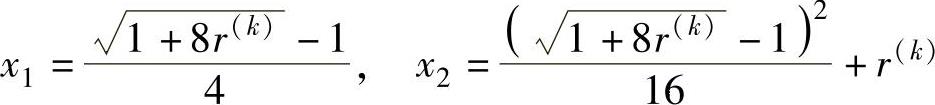(https://www.xing528.com)

当r^（0）=1时，X^（0）=（0.5 1.25）^T，f（X^（0））=1.75；

当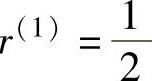时，X^（1）=（0.309 0.782）^T，f（X^（1））=1.09；

当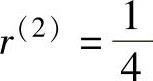时，X^（2）=（0.183 0.283）^T，f（X^（2））=0.466；

当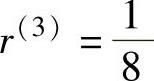时，X^（3）=（0.103 0.135）^T，f（X^（3））=0.238；

︙

当r^（k）=0时，X（k）=（0 0）^T，f（X^（k））=0。

由此可知，X^∗=X^（k）=（0 0）^T，f（X^∗）=f（X^（k））=0就是所求约束优化问题的最优解。惩罚函数的极小点向最优点的逼近路线如图3-25中的虚线所示。

2.外点惩罚函数法

外点惩罚函数法简称外点法。这种方法和内点法相反，新目标函数定义在可行域之外，序列迭代点从可行域之外逐渐逼近约束边界上的最优点。外点法可以用来求解含不等式和等式约束的优化问题。

对于约束优化问题

minf（X），X∈Rⁿ

s.t.g_j（X）≥0 （j=1，2，…，m）

h_k（X）=0 （k=1，2，…，p＜n）

转化后的外点惩罚函数的形式为

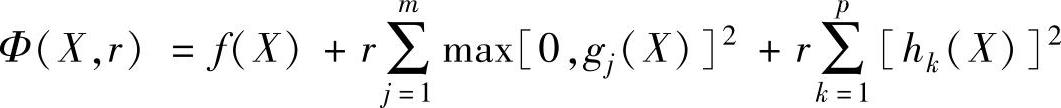
式中的惩罚因子r是由小到大，且趋向于无穷大的数列，即

r^（0）＜r^（1）＜r^（2）＜…→∞

由惩罚项的形式可知，当迭代点并不可行时，惩罚项的值大于零。使得惩罚函数Φ（X，r）大于原目标函数，这可看成是对迭代点不满足约束条件的一种惩罚。当迭代点离边界越远，惩罚项的值越大。但当迭代点不断接近约束边界和等式约束面时，惩罚项的值减小，且趋近于0，惩罚项的作用逐渐消失，迭代点也就趋近于约束上的最优点了。

外点法的收敛条件与内点法相同，其计算步骤除了更换惩罚函数的形式，其他的也与内点法相似。但是在选取迭代参数的时候需要注意几个事项。

1）惩罚因子是一个递增数列，r^（k+1）=cr^（k），其中c为递增系数，通常取c=5～10。

2）r^（0）和c的选取也非常重要。通常情况下取r^（0）=1，c=10可以取得满意结果。也可根据经验公式来计算r^（0）值

式中，。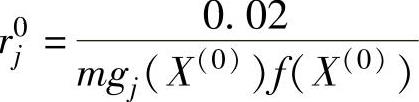

3）约束裕量。外点法是在可行域外寻优的，在可行域外所有的迭代点都是非可行点，其最优点X^∗尽管靠近边界，但也是非可行点。为使X^∗成为可行点，可将每个约束都加上一个裕量，即g_j（X）′=g_j（X）+δ≤0。

例3-9 用外点惩罚函数法求解例3-8。

解 1）构造惩罚函数的无约束优化问题

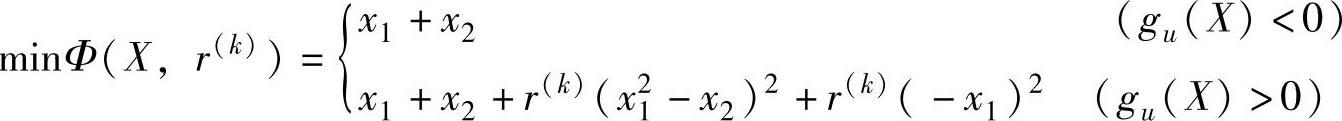
2）用极值条件求解：在可行域内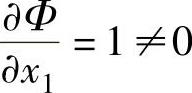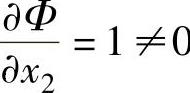，，，知可行域内无极值点。在可行域外，令

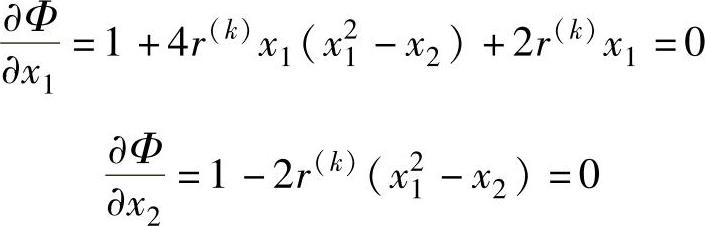
联立求解，得

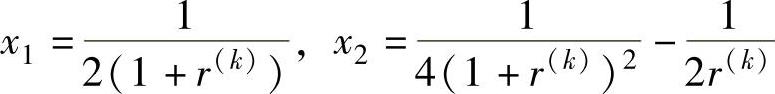
当r^（1）=1时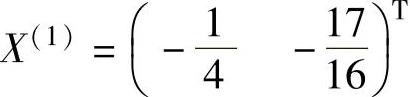，，f（X^（1））=-0.6875；

当r^（2）=2时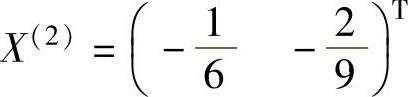，，f（X^（2））=-0.389；

当r^（3）=3时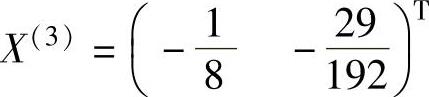，，f（X^（3））=-0.276；

当r^（4）=4时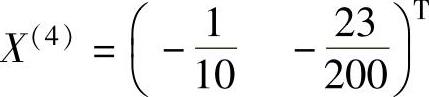，，f（X^（4））=-0.215；

︙

当r^（k）=∞时，X^（k）=（0 0）^T，f（X^（k））=0。

由此可知，X^∗=X^（k）=（0 0）^T，f（X^∗）=f（X^（k））=0就是所求约束优化问题的最优解。惩罚函数的极小点向最优点的逼近路线如图3-26中的虚线①所示。

3.混合惩罚函数法

混合惩罚函数法简称混合法，这种方法是将内点法和外点法结合起来，实现取长补短的效果的一种方法。转化后的混合惩罚函数的形式为

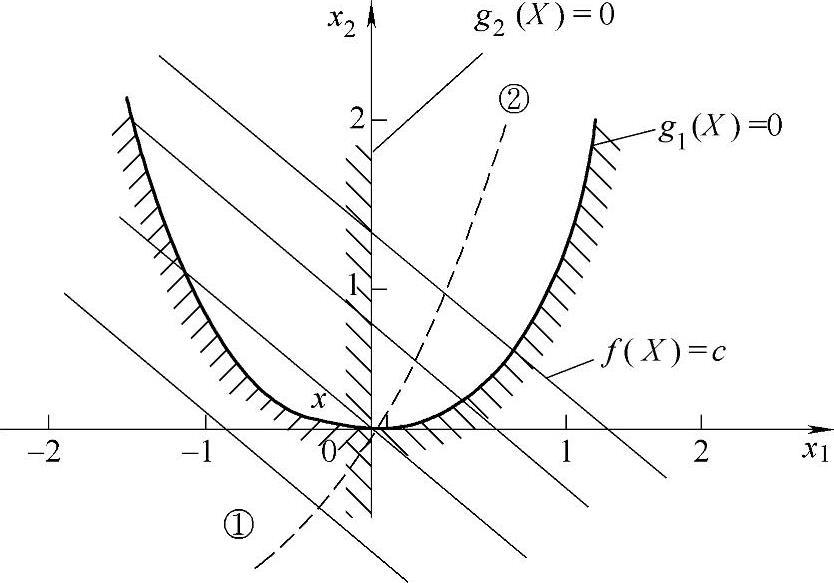
图3-26 外点法的迭代路线

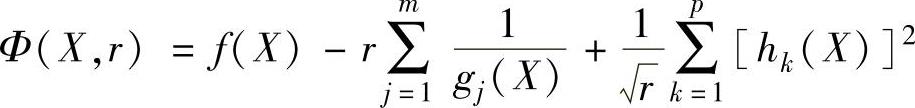
式中，惩罚因子r按内点法选取，即r^（0）＞r^（1）＞r^（2）＞…＞r^（k）＞r^（k+1）＞…≥0。混合法具有内点法的求解特点，即迭代过程在可行域内进行，因此初始点，惩罚因子初值的选取都可以参考内点法的方法来选取。计算步骤也与内点法相似。