复合形法在数值计算中的应用

在可行域中选取两个设计点（n+1≤k≤2n）作为初始复合形的顶点，比较两顶点目标函数值的大小，去掉目标函数值最大的顶点（称最坏点）。以坏点以外其余各点的中心为映射中心，用坏点的映射点替换该点，构成新的复合形顶点。反复迭代计算，使复合形不断向最优点移动和收缩，直至收缩到复合形的顶点与形心非常接近，且满足迭代精度要求为止。另外，初始复合形产生的全部k个顶点必须都在可行域内。

由于复合形的形状不必保持规则的图形，对目标函数及约束函数的性状又无特殊要求，因此该法的适应性较强，在优化设计中得到广泛应用。

1.初始复合形的构成

复合形法是在可行域内直接搜索最优点，所以要求第一个复合形的k个顶点必须都是可行点。图3-23所示为二维问题的复合形。对复合形的顶点数一般取k≈2n，当计算问题的维数n较多（如n＞5）时，可取k=n+1。

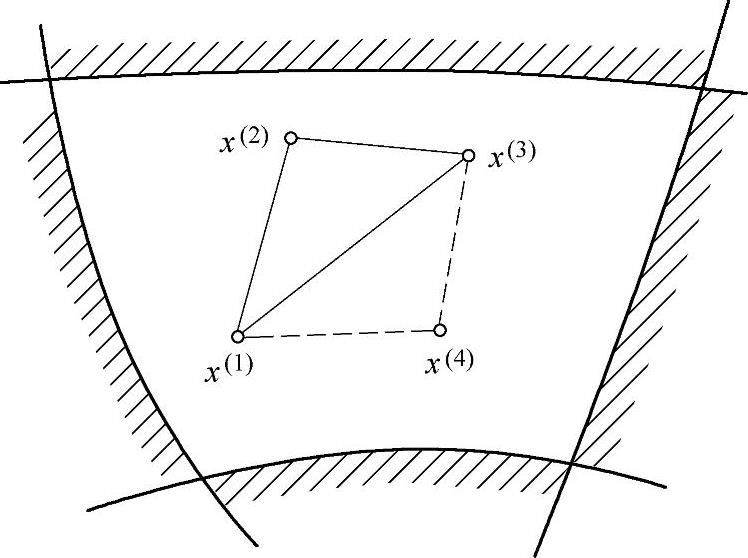
图3-23 二维问题的复合形

初始复合形的构造方法有如下几种：

1）给定k个初始顶点。由设计者预先选择k个设计点，即人工构造一个初始复合形。当设计变量较多或者约束函数复杂时，由设计者决定k个可行点是非常困难的。只有在设计变量少、约束函数简单的情况下，这种方法才被采用。

2）设计者给定一个初始点，其他k-1个顶点可用随机法产生。各顶点按下式计算

x_i^（j）=a_i+r_i^（j）（b_i-a_i） （i=1，2，…，n；j=2，3，…，k）

式中，a_i、b_i为各设计变量的上、下限，一般可取边界约束值；r_i^（j）为[0，1]区间内服从均匀分布伪随机数。

这样随机产生的k-1个顶点，虽然可以满足边界约束条件，但不一定能满足性能约束条件，还必须逐个进行检查，把不满足约束条件的顶点移到可行域内。设已有q个顶点满足全部约束条件，先求出q个顶点的中心点

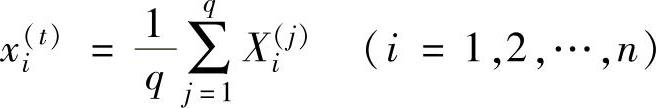
然后将不满足约束条件的点X^（q+1）向中心点X^（t）靠拢，即

X^（q+1）=X^（t）+0.5（X^（q+1）-X^（t））

若还不满足约束条件，则可以重复用上式计算。只要中心点X^（t）是可行点，X^（q+1）点经逐步向X^（t）靠拢，最终总能成为一个可行顶点，从而构成初始复合形。

事实上，只要可行域是凸集，其中心点必为可行点，因而用上述方法可以成功地在可行域内构成初始复合形。如果可行域为非凸集那就有失败的可能，当中心点处于可行域之外时，就应该缩小随机选点的边界域，重新产生各顶点。

3）随机产生全部顶点。先随机产生一个可行点，然后按第二种方法产生其余的k-1个可行点。这样的设计方法比较简单，但因初始复合形在可行域内的位置不能控制，可能会给以后的计算带来困难。

2.复合形法的搜索方法

改变复合形形状的搜索方法主要有以下几种：

（1）反射 反射是改变复合形形状的一种主要方法，其计算步骤为：

1）计算复合形各顶点的目标函数值，并比较其大小，求出最好点X_L、最坏点X_H及次坏点X_G，即

X_L：f（X_L）=min{f（X）_j），j=1，2，…，k}

X_H：f（X_H）=max{f（X_j），j=1，2，…，k}

X_C：f（X_G）=max{f（X_j），j=1，2，…，k，j≠H}

2）计算除去最坏点X_H外的k-1个顶点的中心XC

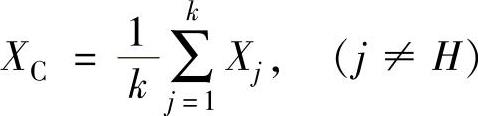
3）从统计的观点来看，一般情况下，最坏点X_H和中心点X_C的连线方向为目标函数下降的方向。为此，以X_C点为中心，将最坏点X_H按一定比例进行反射，有希望找到一个比最坏点X_H的目标函数值小的新点X_R，X_R称为反射点。其计算公式为

X_R=X_C+α（X_C-X_H） （3-19）

式中，α为反射系数，一般取α=1.2～1.4。

4）判别反射点X_R的位置。(www.xing528.com)

①若X_R为可行点，则比较X_R和X_H两点的目标函数值，如果f（X_R）＜f（X_H），则用X_R取代X_H构成新的复合形，完成一次迭代；如果，f（X_R）≥f（X_H），则将α缩小7/10，用式（3-19）重新计算新的反射点，若仍不可行，继续缩小α，直至f（X_R）＜f（X_H）为止。

②若X_R为非可行点，则将α缩小7/10，再用X_R=X_C+α（X_C-X_H）计算反射点X_R，直至可行为止。然后重复以上步骤，即比较X_R和X_H的大小，一旦f（X_R）＜f（X_H），就用X_R取代X_H完成一次迭代。

综上所述，反射成功的条件是

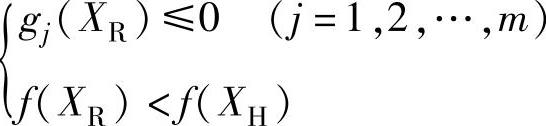
（2）扩张 当求得的反射点X_R为可行点，且目标函数值下降较多，则沿反射方向继续移动，即采用扩张的方法，可能找到更好的新点X_E，X_E称为扩张点。其计算公式为

X_E=X_R+γ（X_R-X_C）

式中，γ为扩张系数，一般取γ=1。

若扩张点X_E为可行点，且f（X_E）＜f（X_R），则称扩张成功，用X_E取代X_R，构成新的复合形。否则称扩张失败，放弃扩张，仍用原反射点X_R取代X_H，构成新的复合形。

（3）收缩 若在中心点X_C以外找不到好的反射点，还可以在X_C以内，即采用收缩的方法寻找较好的新点X_K，X_K称为收缩点。其计算公式为

X_K=X_H+β（X_C-X_H）

式中，β为收缩系数，一般取β=0.7。

若f（X_K）＜f（X_H），则称收缩成功，用X_K取代X_H构成新的复合形。

（4）压缩 若采用上述各种方法均无效，还可以采取将复合形各顶点向最好点X_L靠拢，即采用压缩的方法来改变复合形的形状。压缩后的各顶点的计算公式为

X_j=X_L-0.5（X_L-X_j） （j=1，2，…，k；j≠L）

然后，再对压缩后的复合形采用反射、扩张或收缩等方法，继续改变复合形的形状。

应当指出的是，采用改变复合形形状的方法越多，程序设计越复杂，有可能降低计算效率及可靠性。因此，程序设计时，应针对具体情况，采用某些有效的方法。

3.复合形法的搜索步骤

基本的复合形法（只含反射）的搜索步骤为：

1）选择复合形的顶点数k，一般取n+1≤k≤2n，在可行域内构成具有k个顶点的初始复合形。

2）计算复合形各顶点的目标函数值，比较其大小，找出最好点X_L、最坏点X_H及次坏点X_G。

3）计算除去最坏点X_H以外的k-1个顶点的中心X_C。判别X_C是否可行，若X_C为可行点，则转步骤4）；若X_C为非可行点，则重新确定设计变量的下限和上限值，即令

a=X_L，b=X_C

然后转到步骤1），重新构造初始复合形。

4）按式（3-19）计算反射点X_R，必要时，改变反射系数α的值，直至反射成功。然后以X_R取代X_H，构成新的复合形。

5）若收敛条件

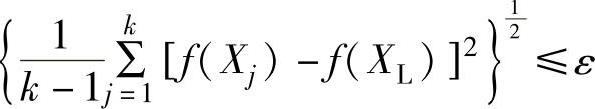
得到满足，计算终止。约束最优解为：X^∗=X_L，f（X^∗）=f（X_L）。否则转到步骤2）。

复合形法的计算框图如图3-24所示。

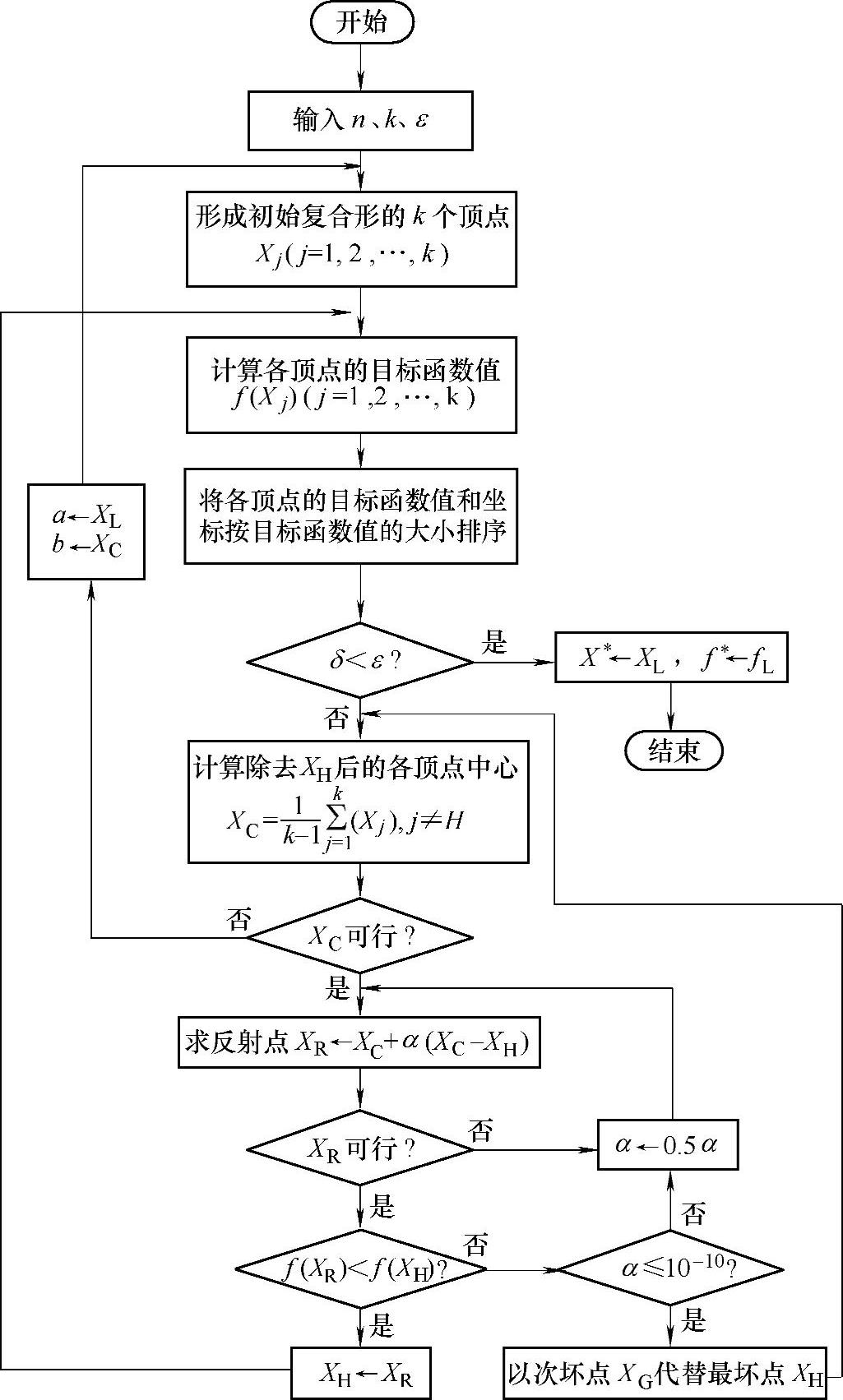
图3-24 复合形法的计算框图