优化目标函数的坐标轮换法

坐标轮换法又称变量轮换法，是无约束最优化直接方法中的一种。坐标轮换法是每次搜索只允许一个变量变化，其余变量保持不变，即沿坐标方向轮流进行搜索的寻优方法，它把多变量的优化问题轮流地转化成单变量的优化问题。该方法在搜索过程中不需要求目标函数的导数，只需目标函数值信息，这就使得该方法相对其他优化方法变得更加简单易行。

下面先以二元函数f（x₁，x₂）为例说明坐标轮换法的寻优过程。

如图3-10所示，从初始点x₀^（0）出发，沿第一个坐标方向搜索，即S₁^（0）=e₁得x₁^（0）=x₀^（0）+α₁^（0）S₁^（0），按照一维搜索方法确定最佳步长因子α₁^（0）满足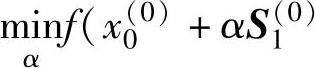：），然后从x₁^（0）出发沿S₂^（0）=e₂方向搜索得x₂^（0）=x₁^（0）+α₂^（0）S₂^（0），其中步长因子α₂^（0）满足：minf（x₁^（0）+αS₂^（0）），x₂^（0）为一轮迭代（k=0）的终点。在这里x的上标表示迭代点的轮号，每做完n次变量的一维搜索，称一轮；下标表示迭代点的序号。检验始、终点间距离是否满足精度要求，即判断‖x₂^（0）-x₀^（0）‖＜ε的条件是否满足。若满足则x⁰₂→x^∗否则x⁰₂→x₀¹，重新依次沿坐标方向进行下一轮（k=1）的搜索。

图3-10 坐标轮换法的搜索过程

对于n个变量的函数，若在第k轮沿第i个坐标方向S_i^（k）进行搜索，其迭代公式为

x_i^（k）=x_i-1^（k）+α_i^（k）S_i^（k）（k=0，1，2，…；i=1，…，n） （3-3）

其中，搜索方向取坐标方向，即S_i^（k）=e_i（i=1，…，n）。若‖x_n^（k）-x₀^（k）‖＜ε，则x_n^（k）→x^∗；否则x_n^（k）→x₀^（k+1），进行下一轮搜索，直到满足精度要求为止。

坐标轮换法的优化性能在很大程度上取决于目标函数的形态。如果目标函数为二元二次函数，其等值线为圆或长短轴平行于坐标轴的椭圆时，此法很有效，一般经过两次搜索即可达到最优点，如图3-11a所示。如果等值线为长短轴不平行于坐标轴的椭圆，则需多次迭代才能达到最优点，如图3-11b所示。如果等值线出现脊线，本来沿脊线方向一步可达到最优点，但因坐标轮换法总是沿坐标轴方向搜索而不能沿脊线搜索，所以就终止到脊线上而不能找到最优点，如图3-11c所示。(www.xing528.com)

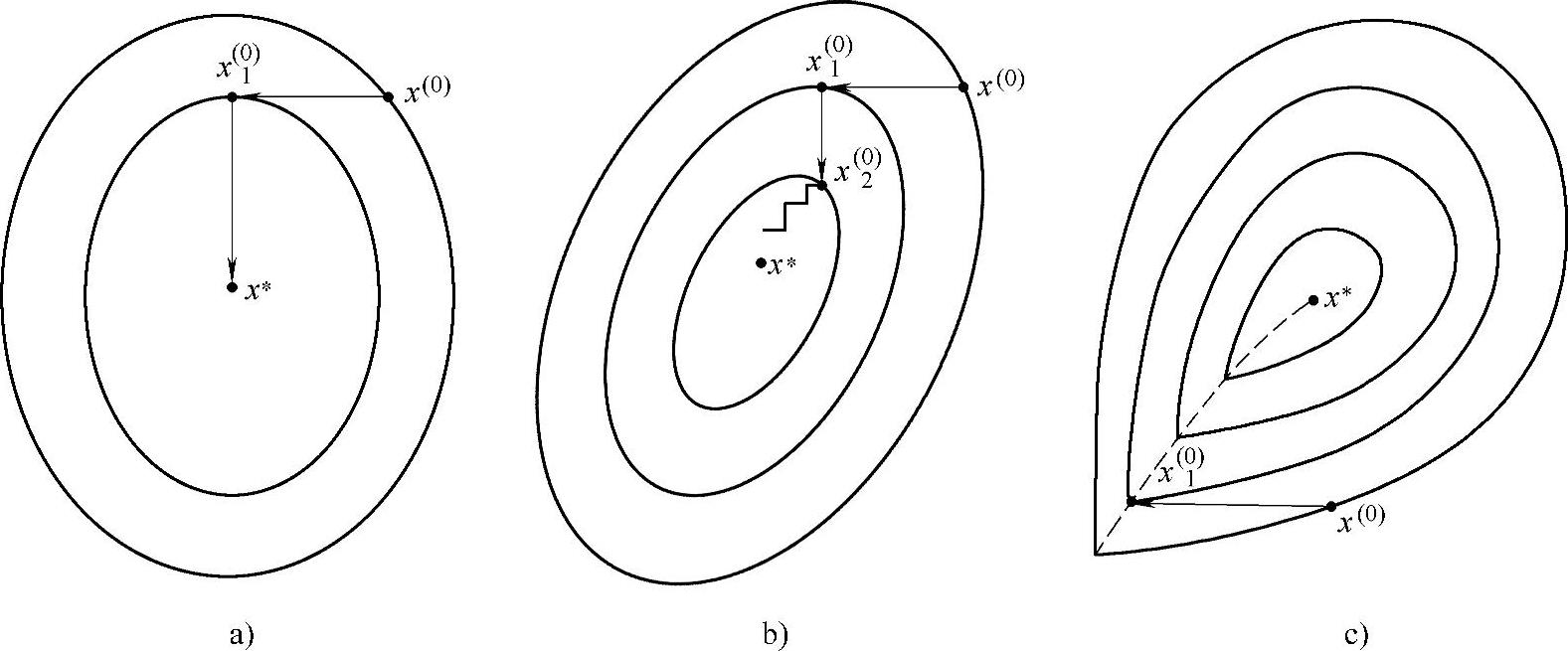
图3-11 搜索过程的几种情况

从上述分析可以看出，采用坐标轮换法只能轮流沿着坐标方向搜索，尽管也能使函数值步步下降，但要经过多次曲折迂回的路径才能达到极值点，尤其在极值点附近步长很小，收敛很慢，所以坐标轮换法不是一种很好的搜索方法。

根据坐标轮换法的搜索原理，鲍威尔（Powell）提出了一种具有加速收敛的更好的搜索算法——鲍威尔法。

坐标轮换法的计算框图如图3-12所示。

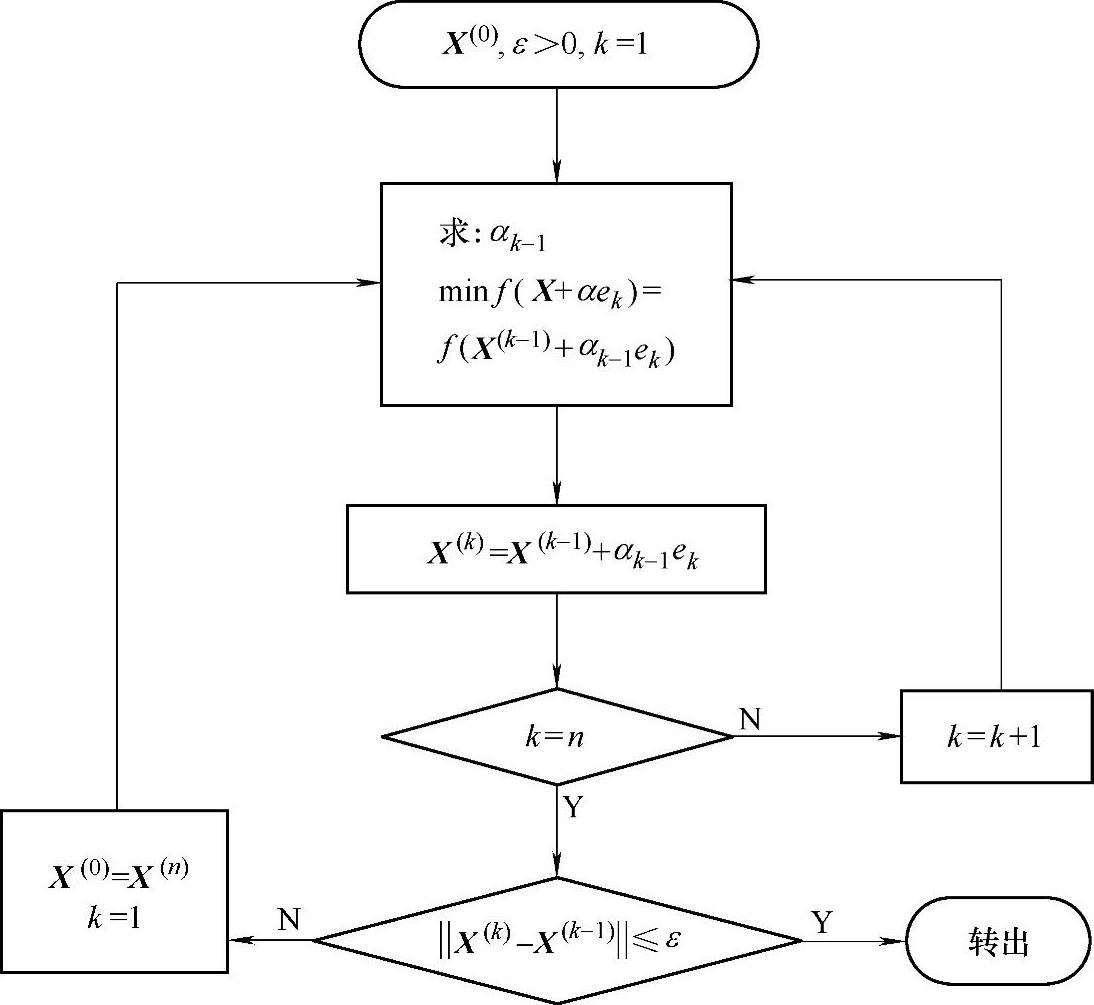
图3-12 坐标轮换法的计算框图